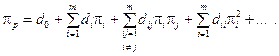Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекція №7. Подібність при моделюванні.Стр 1 из 5Следующая ⇒
Лекція №7. Подібність при моделюванні. Види моделей. Фізичне, аналогове Та математичне моделювання Критерії механічної і гідродинамічної подібності
Теорема вказує на можливість свого роду заміни змінних і скорочення їх кількості з
Таблиця 7.2 Критерії електричної подібності
Таблиця 7.3 Види моделей Теорія подібності і моделювання, що є, по суті, теорією постановки і обробки експериментальних та аналітичних досліджень, здатна значною мірою вирішити багато труднощів, що виникають при цьому. І все жё подібність і моделювання не можуть стати і не стали окремою спеціальною наукою, хоча в гносеологічному плані виділяють деякі загальні властивості, властиві всім моделям. Ці властивості полягають в наявності деякої структури статичною і динамічною, яка подібна або розглядається як подібна структури іншої системи. Будь-яка модель, таким чином, це природний або штучний об'єкт, що знаходиться у відповідності з об'єктом, що вивчається, або якою-небудь із його сторін. В процесі вивчення модель служить відносно самостійним «квазіоб'єктом», що дозволяє отримати при його дослідженні деякі знання про об'єкт, що вивчається. Моделі всіх видів поступово набувають все більшого значення, дозволяючи проводити наукові дослідження різних процесів, уточнювати теорію роботи різного обладнання, перевіряти висновки і отримувати повніше і наочніше уявлення, ніж це можна було б зробити тільки на підставі розрахунку. Моделі мають велике значення з точки зору навчання, дозволяючи неодноразово відтворювати аварійні режими машин, апаратів та систем, вивчаючи при цьому їх у прискореному часі, необхідному для отримання потрібного досвіду. Моделі забезпечують обробку психологічної сумісності нових машин, апаратів та систем і людини. Концептуальні моделі передбачають розробку і використання моделей, що формуються спостереженням в процесі навчання і спостереження за об'єктом під час його функціонування. Моделі дозволяють оцінювати значущість властивостей цілісності, виявляти властивості системи і приходити в деякий стан, який визначається її власною структурою. Іноді виділяють логічні моделі, які будуються за допомогою апарату математичної логіки, а формальна побудова використовується далі для змістовної їх інтерпретації.
Кібернетичні моделі грунтуються на отриманні співвідношень між вхідними і вихідними функціями для якогось чорного або сірого ящика, що представляє явище, що досліджується, без розкриття його внутрішньої структури. Квазіаналогові моделі і електронні моделі займаються синтезом кіл, що є моделями різних об'єктів, мають особливо велике значення в даний час при вирішенні задач, що виникають при проектуванні і експлуатації великих систем технічного призначення. Електронне моделювання дозволяє успішно вирішувати задачі об'єктів і явищ шляхом створення моделі з комбінованих операційних блоків і проведення синтезу моделей. Набір універсальних комбінаційних операційних блоків дозволяє створювати універсальні і спеціалізовані аналогові машини (АВМ), пов’язані з універсальними цифровими обчислювальними машинами (ЕОМ). Останнім часом багато уваги приділяється задачам синтезу на відміну від задач аналізу. Синтез вимагає не просто визначення характеру процесу при заданих його початкових умовах, але визначення таких дій на систему (і таке її моделювання), за яких вдалося б виявити характер і величину дій, що забезпечують в даній системі такий характер процесів, який бажано надати процесам в проектованій або існуючій системі. Модель відкриває великі можливості перевіряти передумови різних співвідношень і припущень, прийнятих при математичному описі різних процесів, що виникають в аварійних умовах, і відтворювати всі дії персоналу в умовах, близьких до природних, необхідних для усунення аварійних ситуацій, тобто здійснити психологічне моделювання операцій. Подібність і моделювання не тільки не суперечать аналітичним методам, що застосовують цифрові обчислювальні машини, але, навпаки, підкріплюють їх, забезпечуючи перевірку аналітичних методів, сприяючи упевненості в їх застосуваннях.
Критерійній формі
Величезні швидкості обчислень сучасних цифрових обчислювальних машин забезпечують бистроту аналітичних рішень. Проте при помилках фізичного або формального характеру цифрова машина може видати так же швидко і упевнено неправильне рішення. Тому особливого значення набуває апробація програм для обчислювальних машин з точки зору коректності закладених в них фізичних положень і правильності неминучих спрощень. Ця перевірка повинна проводитися на основі методів подібності і моделювання. Роль експерименту, а разом з цим і моделювання, збільшується з розвитком і вдосконаленням цифрових обчислювальних машин. Експеримент є не тільки шляхом безпосереднього вирішення тих чи інших науково-технічних завдань, але і допомагає знаходити найкращий засіб аналітичного розв’язку. Моделі різних видів і різного роду (фізичні, аналогові і математичні) повинні застосовуватися спільно і одночасно з цифровими обчислювальними машинами при дослідженні роботи різних технічних систем, аналізі розвитку і управління їх функціонуванням, тобто у всіх галузях наукових і науково-технічних знань звертається увага на створення фізико-цифроаналоговых комплексів, що забезпечують єдиний багатоаспектний підхід до дослідження. Оцінку достовірності будь-якого дослідження, у тому числі і із застосуванням моделювання, дає експеримент, проведений за спеціальною програмою. Критерійна програма проведення експериментів (уявних, математичних або фізичних) дає оцінку результату, що поширюється на клас явищ (а не тільки на одиничні явища) у вигляді узагальненої критерійної залежності, і дозволяє відсіяти вплив сторонніх, випадкових факторів. Особливо вдало розв’язуються задачі, що виникають при вивченні різних складних систем і пов'язані із знаходженням сукупності факторів, що варіюються, при яких цільова функція екстремальна. Методи планування експерименту дозволяють вирішити цю задачу з мінімальною кількістю дослідів при надійній статистичній інтерпретації на кожному етапі. Переваги направленого експерименту, що обробляється в критерійній формі, взагалі великі і істотні також при квазіаналоговому електронному моделюванні, при всіх різновидах математичного моделювання.
Слід звертати увагу на можливість знаходження функцій правдоподібності, тобто певної математичної форми, що допомагає характеризувати результати експерименту, який проводиться як на реальних об’єктах, так і на будь-яких, зокрема квазіаналогових, моделях. Поєднання теорії планування експерименту і теорії подібності дозволяє ввести поняття «критерійна функція відгуку». Тут, проте, на відміну від теорії планування експерименту варіації виконуються не в окремих величинах, а в критерійних співвідношеннях. Такого роду співвідношення дозволяють відразу отримувати області доцільних параметрів. Ці області, представлені у вигляді просторів, будуть особливо важливі при дослідженнях складних систем, що проводяться на квазіаналогових електронних і інших моделях. Розв’язуючи задачі оптимізації, знаходять області, де існують тенденції до певного мінімуму зміни цільової функції. При вивченні великих систем моделювання виступає як могутній засіб безпосереднього зв'язку теорії і досвіду, як інструмент перевірки практикою створюваних теорій і розрахунків методу, як засіб прискорення випробування надійності, перевірки нової, що конструюється, апаратури. Для використання моделювання в технічних, інженерних завданнях істотне значення має автоматизація отримання критеріїв подібності за допомогою обчислювальних машин. Далі моделювання повинне розвиватися при поєднанні методів теорії подібності, планування експерименту, регресійного аналізу, досліджень при ймовірнісній і неповній інформації. Критеріальні залежності у поєднанні з методами планування експерименту і статичними методами полегшують задачі оптимізації складних систем.
Збільшення складності та розмірів систем вимагає постійного вдосконалення моделювання і перевірки отриманих результатів шляхом експерименту. Чітко провести будь-який (фізичний або обчислювальний) експеримент, об'єктивно оцінити відомості про процес, що вивчається, і поширити матеріал, отриманий в одному дослідженні, на серію інших досліджень можна лише у разі правильної їх постановки та обробкиі. Критерійна обробка результатів досліджень дозволяє скоротити кількість необхідних експериментів за рахунок зменшення числа факторів, які варіюються, поширити результати кожного з цих експериментів на необмежено великий клас подібних процесів. Критерійну обробку експериментальних даних при невідомому математичному описі процесу можна показати на одному з прикладів. Хай вивчається процес в електричному колі з активним опором R, індуктивністю L і ємністю С при включенні на джерело постійної напруги U. Треба оцінити вплив варіацій параметрів R, L, C і U в заданих діапазонах на максимальне значення струму в колі, тобто вивчити залежність Перехід до критеріїв подібності зменшує кількість факторів, що варіюються, з чотирьох (R, L, С, U) до одного ( Для визначення критеріїв подібності необхідно знати початкові і граничні значення, значення параметрів режиму, які не змінюються, і т. д.; поточні значення параметрів
а також критеріїв подібності, кожен із яких в чисельнику містить поточне значення параметра
Іноді називають такі критерії вираженими у відносних одиницях параметрами режиму. У рівняннях процесу і початкових (граничних) умовах треба замінити параметри Критерійне планування експерименту (КПЕ) (теорія планування експерименту) і теорія подібності, що сприяють якнайкращій організації експерименту і обробці його результатів, в даний час практично об'єдналися. Нехай, наприклад, потрібно вивчити залежність Для КПЕ необхідно: 1) визначення виду безрозмірних комплексів
Якщо експерименти проводяться в реальній системі або на фізичній моделі, в матрицю КПЕ, що містить в якості варійованих чинників безрозмірні комплекси, необхідно ввести ще значення варійованих параметрів Отриманий в результаті проведення мінімуму дослідів (розрахунків) поліном, що зв'язує безрозмірні комплекси, дозволяє не тільки вивчити конкретну залежність, але і розповсюдити результати цих досліджень на широкий клас процесів.
Лекція №7. Подібність при моделюванні.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 134; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.69.143 (0.034 с.) |

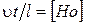
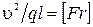






 ─ час;
─ час;  ─ густина рідини;
─ густина рідини; ─ маса;
─ маса;  ─ в'язкість;
─ в'язкість; ─ геометричний розмір;
─ геометричний розмір;  ─ коефіцієнт кінематичної в’язкості;
─ коефіцієнт кінематичної в’язкості; ─ швидкість;
─ швидкість;  ─ потужність турбіни;
─ потужність турбіни; ─ прискорення сили тяжіння;
─ прискорення сили тяжіння;  ─ діаметр;
─ діаметр; ─ сила, тиск;
─ сила, тиск;  ─ тиск;
─ тиск; ─ механічний момент.
─ механічний момент. розмірних до
розмірних до  безрозмірних величин, з переходом до критеріального рівняння. Таким чином, спрощується обробка аналітичних і експериментальних досліджень, оскільки зв'язок між безрозмірними критеріями подібності
безрозмірних величин, з переходом до критеріального рівняння. Таким чином, спрощується обробка аналітичних і експериментальних досліджень, оскільки зв'язок між безрозмірними критеріями подібності  у більшості випадків є простішим. Але не тільки цим визначається значення теореми. Вельми істотно, що перехід до безрозмірних співвідношень дозволяє розповсюдити результати дослідження, проведеного стосовно конкретного явища, на ряд подібних явищ.
у більшості випадків є простішим. Але не тільки цим визначається значення теореми. Вельми істотно, що перехід до безрозмірних співвідношень дозволяє розповсюдити результати дослідження, проведеного стосовно конкретного явища, на ряд подібних явищ.

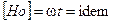

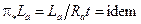




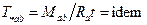





 ─ коефіцієнт магнітної проникності;
─ коефіцієнт магнітної проникності; ─ провідність, питоме середовище;
─ провідність, питоме середовище; ─ діелектрична стала;
─ діелектрична стала; ─ кутова швидкість;
─ кутова швидкість; ─ частота;
─ частота; 
 ─ напруженість поля в точці К;
─ напруженість поля в точці К; ─ індуктивність кола;
─ індуктивність кола; ─ омічний опір;
─ омічний опір;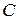 ─ ємність;
─ ємність;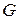 ─ провідність на одиницю довжини електричної лінії;
─ провідність на одиницю довжини електричної лінії; ─ часова стала.
─ часова стала. . Критерії подібності процесу визначаються на основі аналізу розмірності параметрів i, R, L, С, U. Шляхом вибору в якості незалежних параметрів U, R і С можна отримати
. Критерії подібності процесу визначаються на основі аналізу розмірності параметрів i, R, L, С, U. Шляхом вибору в якості незалежних параметрів U, R і С можна отримати  . З урахуванням цих критеріїв залежність, що досліджується, в критерійній формі набуває такого вигляду
. З урахуванням цих критеріїв залежність, що досліджується, в критерійній формі набуває такого вигляду  . Якщо відомий математичний опис процесу, то для наведеного вище прикладу
. Якщо відомий математичний опис процесу, то для наведеного вище прикладу  . Діленням всіх членів рівняння на четвертий член можна отримати три критерії подібності:
. Діленням всіх членів рівняння на четвертий член можна отримати три критерії подібності: 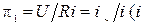 ─ це усталений струм у колі),
─ це усталений струм у колі),  . Якщо об'єднати другий і третій критерії в один, то при незмінному масштабі часу
. Якщо об'єднати другий і третій критерії в один, то при незмінному масштабі часу  критерій
критерій  визначає масштаб струму
визначає масштаб струму  . Таким чином, отримуємо той же результат, що і на основі аналізу розмірностей.
. Таким чином, отримуємо той же результат, що і на основі аналізу розмірностей. ). Це скорочує число дослідів, необхідних для експериментального визначення шуканої залежності. Три-чотири досліди за умов варіації значень безрозмірного комплексу дають співвідношення, що виявляє вплив на параметри R, L, С, U. Кожна точка цього співвідношення відповідатиме нескінченній кількості подібних процесів
). Це скорочує число дослідів, необхідних для експериментального визначення шуканої залежності. Три-чотири досліди за умов варіації значень безрозмірного комплексу дають співвідношення, що виявляє вплив на параметри R, L, С, U. Кожна точка цього співвідношення відповідатиме нескінченній кількості подібних процесів 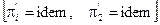 .
. ; скласти матрицю розмінностей А всіх задіяни в процесі параметрів
; скласти матрицю розмінностей А всіх задіяни в процесі параметрів 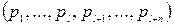 і визначити ранг цієї матриці; вибрати в якості незалежних параметрів R величин. Все це дає можливість визначити на основі аналізу розмірностей відповідну форму запису безрозмірних комплексів вигляду
і визначити ранг цієї матриці; вибрати в якості незалежних параметрів R величин. Все це дає можливість визначити на основі аналізу розмірностей відповідну форму запису безрозмірних комплексів вигляду



 на одиниці, параметри
на одиниці, параметри  ─ на безрозмірні комплекси
─ на безрозмірні комплекси 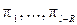 , а поточні значення
, а поточні значення 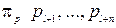 ─ на виражені у відносних одиницях. Наявність критеріїв подібності дає можливість відповідним чином спланувати проведення експерименту.
─ на виражені у відносних одиницях. Наявність критеріїв подібності дає можливість відповідним чином спланувати проведення експерименту. , яка зв'язує цільову функцію експерименту (наприклад, яке-небудь експериментальне значення параметра) із значеннями інших параметрів.
, яка зв'язує цільову функцію експерименту (наприклад, яке-небудь експериментальне значення параметра) із значеннями інших параметрів. , виражених у відносних одиницях
, виражених у відносних одиницях  , та критеріальної цільової функції (якщо диференціальні рівняння процесу відомі, слід перетворити ці рівняння в початкові (граничні) умови і звести їх до критерійного вигляду відповідно до описаного вище способу); 2) визначення діапазонів варіювання безрозмірних комплексів за заданими інтервалами варіювання параметрів
, та критеріальної цільової функції (якщо диференціальні рівняння процесу відомі, слід перетворити ці рівняння в початкові (граничні) умови і звести їх до критерійного вигляду відповідно до описаного вище способу); 2) визначення діапазонів варіювання безрозмірних комплексів за заданими інтервалами варіювання параметрів 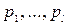 , 3) виявлення домінуючих безрозмірних комплексів
, 3) виявлення домінуючих безрозмірних комплексів  шляхом проведення дослідів (розрахунків) відповідно до матриці критерійного планування відсіваючого експерименту; 4) проведення дослідів (розрахунків) у відповідності з матрицею критерійного планування активного або пасивного експерименту з метою визначення коефіцієнтів полінома:
шляхом проведення дослідів (розрахунків) відповідно до матриці критерійного планування відсіваючого експерименту; 4) проведення дослідів (розрахунків) у відповідності з матрицею критерійного планування активного або пасивного експерименту з метою визначення коефіцієнтів полінома: