
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Загальні умови стабілізації державного боргуСодержание книги Поиск на нашем сайте
Аналіз рівняння (2.5.9) показує, зокрема, що коли монетарні інструменти не використовуються (S = 0), то стабілізація державного боргу може забезпечуватися лише проведенням послідовної чи збалансованої бюджетної політики, яку можна подати такою умовою:
Тут ідеться про те, що сплата боргів і фінансування поточних урядових витрат можливі лише тоді, коли потік приведеної вартості майбутніх податків не менший від потоку витрат. Теоретичні аспекти цієї проблеми ретельно досліджені С. Тарновським[2]. Зазначимо, що припущення щодо можливості нульового сеньйоражу вимагає фінансування операційного дефіциту, тобто суми поточного дефіциту й обслуговування боргу цілком за рахунок розміщення нових боргів на вільному ринку. Така ситуація може бути правдоподібною лише за умови високої кредитоспроможності уряду, відносно невеликих обсягів його боргів і частки дефіциту у ВВП країни. У більш загальних ситуаціях держава, очевидно, не може нехтувати монетарними інструментами для фінансування своїх витрат, зокрема, для обслуговування накопиченого боргу. У перехідний період держава, власне, і не здатна на таке внаслідок як значних масштабів фінансування дефіциту, так і нерозвинутості фінансового ринку та обмеженої довіри до її політики. Спільне використання емісії грошей і боргів як джерела фінансування дефіциту приводить до двох важливих наслідків: сеньйораж стає, по-перше, основним джерелом формування купонних виплат приватним інвестором і, по-друге — засобом регулювання обсягів боргових зобов’язань. Остання функція сеньйоражу випливає з того, що за фінансової ставки загальної дохідності облігацій більша купонна дохідність означає меншу величину зростання капітальної вартості активів, і навпаки. Нехай величина (обсяг) поточного бюджетного дефіциту в реальному вираженні є додатною функцією часу. Якщо сеньйораж не перевищує обсяги поточного бюджету, тобто має місце нерівність
то, як показує розв’язок рівняння (2.5.9), державний борг зростає необмежено. Така ситуація пояснюється тим, що держава розміщує на вільному ринку додаткові борги в облігаціях, що більші чи дорівнюють обсягам, необхідним для сплачення боргів у даний момент часу, тобто існуючі борги мовби «забезпечуються» майбутніми боргами. В цьому випадку держава проводить так звану гру Понці (фінансова піраміда), ірраціональність якої для b (0) = b 0, r > 0, Sn < 0 відображається в нестійкості розв’язку рівняння
Розглядаючи це рівняння з позиції приватного інвестора, можна дійти висновку, що ігри Понці є можливими, якщо інвестор згоден купувати активи (борги уряду) чи очікуючи лише зростання їхньої капітальної вартості, чи згоджуючись мати поточні збитки (від’ємний купонний дохід). Ясно, що попереднє твердження погано узгоджується з дійсністю, а тому ситуації, що породжують ігри Понці, необхідно виключати. Отже, інтерес з погляду раціональної макроекономічної політики становлять лише стійкі розв’язки рівняння (2.5.9).
2.5.7. Стійкий розв"язок рівняння боргу Коли сеньйораж є більшим за реальний поточний дефіцит:
то обсяг розміщення боргових зобов’язань буде меншим за величину обслуговування поточного боргу. Тому отримати стійкий розв’язок рівняння (2.5.9) за позитивного значення норми реальної дохідності облігацій r > 0 можливо лише за умови, що обсяги сеньйоражу перевищуватимуть реальний дефіцит бюджету. В цьому випадку загальні обсяги боргових зобов’язань можуть регулюватися, зокрема, через проведення певної монетарної політики. Наприклад, обсяги сеньйоражу можуть бути встановлені на такому рівні, щоб покривати бюджетний дефіцит і нові запозичення. За відомого потоку майбутнього «чистого» сеньйоражу SN = SN (t) та виконання умови збіжності звичайне диференціальне рівняння
яке можна записати в еквівалентній інтегральній формі
що легко перевірити диференціюванням, тут розв’язок (16.12) параметрично залежить від функції SN (t). Розв’язок (2.5.12) має глибокий економічний зміст. Якщо невласний інтеграл у його правій частині сходиться, то у цьому випадку він являє собою дисконтовану за дохідністю r > 0 до поточного моменту t поточну вартість майбутнього потоку сеньйоражу. Тобто b (t, S) — це ринкова вартість державного боргу, яка є скінченною величиною, незважаючи на невід’ємність параметра дохідності (r > 0). Отже, використання в економічних обчисленнях і в прийнятті економічно обґрунтованих рішень на перспективу ринкової вартості боргу є цілком виправданим і обґрунтованим, оскільки відображає в кожен момент часу можливість еволюції, наприклад перепродажу, боргу в майбутньому. Це робить вираз (2.5.12) надзвичайно зручним в економічних розрахунках і моделюванні. Для відомої (фіксованої) функції сеньйоражу маємо b (t, S) =
де А — довільна константа інтегрування, яка добирається так, щоб виконувалася умова
Виконання цієї умови забезпечує збіжність невласного інтеграла Треба наголосити, що рівняння (2.5.11) є, власне, умовою арбітражу, що розглядалось у підрозд. 2.5.3. З погляду приватного інвестора це рівняння формує ринкові вимоги щодо дохідності державного боргу. З погляду уряду умова
стверджує, що потреба в обслуговуванні поточного боргу (rb) визначає обсяги як сеньйоражу
Випадок нульової купонної дохідності потрібно вилучити з міркувань недопустимості ігор Понці (фінансових пірамід), тимчасом як випадок r = d відповідає стаціонарній точці для (2.5.11). Зрозуміло, що уряд як монопольний емітент боргових зобов’язань свою коротку позицію на ринку облігацій може забезпечити, лише переконавши приватних інвесторів зайняти довгу позицію. З погляду приватних інвесторів — власників реальних грошових балансів і реальних боргів держави — безризикова норма відсотка диктує загальні вимоги інвесторів до дохідності державних облігацій, тоді як сеньйораж забезпечує їхні поточні доходи чи купонні виплати. За заданих значень r і d загальна фінансова збалансованість визначатиметься обсягом нових позик чи зміною капітальної вартості активів a, де r = d + a. Викладене вище означає, зокрема, що майбутній потік зростаючого з постійним темпом сеньйоражу фактично дисконтується за ставкою купонних виплат. Нехай у розв’язку (2.5.12) купонні виплати зростають з постійним темпом
тоді для t ³ t та кожного t маємо
звідки й отримуємо справедливість співвідношення Розгляньмо ще одну умову, котра дозволяє дещо спростити модель, не порушуючи її економічної загальності. З наведених вище міркувань випливає, що реалізація послідовної бюджетної політики вимагає рівності між приведеною поточною вартістю сеньйоражу й податків, з одного боку, і ринковою вартістю бор-
Уважаючи, що дисконтовані вартості потоків майбутніх податків і бюджетних витрат дорівнюють одне одному, отримаємо, що ринкова вартість боргу — це приведена поточна вартість потоку майбутнього сеньйоражу:
Умова (2.5.13), яка дозволяє розглянути залежність між сеньйоражем і боргом, широко використовується в наукових дослідженнях для більш адекватного, в стохастичній постановці, формулювання проблеми. Зрозуміло, що величина (2.5.13) параметрично залежить від потоку сеньйоражу, тож у загальному випадку має місце
Для (2.5.14) стаціонарний стан визначається як b (t, S) = b (S) і дорівнює
За умови, що сеньйораж зростає з постійним темпом a > 0, який пов’язаний з купонним доходом d > 0 і безризиковою ставкою дохідності облігацій r > 0 співвідношенням
ринкова вартість державного боргу в стаціонарному стані являє собою величину
яка відіграє важливу роль у стохастичних моделях динаміки
|
||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 227; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.56.71 (0.008 с.) |

 (2.5.10)
(2.5.10)


 , (2.5.11)
, (2.5.11) (2.5.12)
(2.5.12)
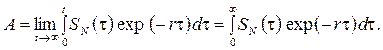
 який є стійким розв’язком для рівняння (2.5.11).
який є стійким розв’язком для рівняння (2.5.11).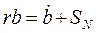
 , так і додаткового розміщення боргів (b) на вільному ринку. Закріплення норм дохідності або ринком, або політикою обмежує привабливість нових облігацій, а отже, можливості держави щодо розміщення додаткових боргів. У цьому випадку природно вважати, що уряд може брати в борг лише за умови 0 < a < r, тобто купонна дохідність є додатною:
, так і додаткового розміщення боргів (b) на вільному ринку. Закріплення норм дохідності або ринком, або політикою обмежує привабливість нових облігацій, а отже, можливості держави щодо розміщення додаткових боргів. У цьому випадку природно вважати, що уряд може брати в борг лише за умови 0 < a < r, тобто купонна дохідність є додатною:
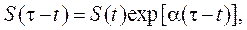

 , зокрема, можливість подання боргу як величини, пропорційної сеньйоражу.
, зокрема, можливість подання боргу як величини, пропорційної сеньйоражу.
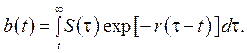 (2.5.13)
(2.5.13) (2.5.14)
(2.5.14)
 ,
, або
або 



