Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Д. У. Движения МТ. Первая и вторая задачи динамики точки.
Д.У. движения МТ. Первая и вторая задачи динамики точки. Положение МТ в инерциальной с.о. будем определять ее радиус-вектором r. Сила F, действующая на точку, может зависеть от положения точки, т. е. от r, скорости
В зависимости от выбора осей координат, на к-рые проектируется осн.ур-е динамики можно получить разл. формы скалярных д.у. дв-я МТ. В декарт.сис-ме: В случае плоского дв-я точки, рассматр. в полярных координатах, имеет вид
С помощью осн.ур-я динамики решаются 2 осн.задачи динамики: 1) Когда дв-е задано, известна масса, необходимо найти силу, под действием которой происходит дв-е. Решение: закон движения подставляется в д.у. и с помощью дифференцирования соотв.функций определяются проекции силы; 2) Когда по известным приложенным силам и массе находят закон движения МТ. Решение: осн.ур-е динамики необходимо проинтегрировать дважды (сила зависит от времени, от скорости, пропорциональна координате) Полная работа. Полная работа силы тяжести и упругости. Полная работа – работа внешних и внутренних сил, приложенных к МС: А=Ае+Аi Работа сил тяжести. Если МС находится в однородном поле тяжести, то на каждую ее точку Мk действует внешняя сила Работа силы упругости. Рассмотрим силы упругой пружины, коэф.жестк.С. вычислим работу при растяжении пружины на длину f из нерастянутого состояния. Как и в случае для силы тяжести, работа сил упругости не зависит от траектории. Теорема об изменении кинетической энергии точки. Найдем связь между работой сил, приложенных к МТ, изменением скорости точки. Для этого воспользуемся основным уравнением динамики.
- изменение кинетической энергии МТ на каком-либо ее перемещении = сумме работ всех сил, действующих на МТ на том же перемещении. Теорема Штейнера-Гюйгенса. Существует простая связь между моментами инерции тела относительно параллельных осей, одна из которых проходит через центр масс. Эта связь устанавливается теоремой Гюйгенса-Штейнера: момент инерции тела относительно некоторой оси равен сумме момента инерции тела относительно оси проходящей через центр масс параллельно данной, и произведения массы тела на квадрат расстояния между ними Общее уравнение динамики.
Д.У. движения МТ. Первая и вторая задачи динамики точки. Положение МТ в инерциальной с.о. будем определять ее радиус-вектором r. Сила F, действующая на точку, может зависеть от положения точки, т. е. от r, скорости
В зависимости от выбора осей координат, на к-рые проектируется осн.ур-е динамики можно получить разл. формы скалярных д.у. дв-я МТ. В декарт.сис-ме: В случае плоского дв-я точки, рассматр. в полярных координатах, имеет вид
С помощью осн.ур-я динамики решаются 2 осн.задачи динамики: 1) Когда дв-е задано, известна масса, необходимо найти силу, под действием которой происходит дв-е. Решение: закон движения подставляется в д.у. и с помощью дифференцирования соотв.функций определяются проекции силы; 2) Когда по известным приложенным силам и массе находят закон движения МТ.
Решение: осн.ур-е динамики необходимо проинтегрировать дважды (сила зависит от времени, от скорости, пропорциональна координате)
|
||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 204; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.205.154 (0.005 с.) |
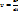 и времени t. Следовательно, в общем случае
и времени t. Следовательно, в общем случае 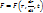 и основное уравнение динамики mw=F точки можно записать в следующей форме:
и основное уравнение динамики mw=F точки можно записать в следующей форме: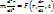 – дифференциальное ур-е дв-я в векторной форме (r-функция, t-аргумент).
– дифференциальное ур-е дв-я в векторной форме (r-функция, t-аргумент).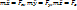
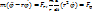 , где Fr и Ff – проекции силы на напр-е радиус-вектора и перпендикулярное к нему напр-е. Аналогично можно получить записи д.у. в др.сис-мах координат.
, где Fr и Ff – проекции силы на напр-е радиус-вектора и перпендикулярное к нему напр-е. Аналогично можно получить записи д.у. в др.сис-мах координат.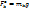 . Тогда элементарная работа внешних сил будет равна
. Тогда элементарная работа внешних сил будет равна 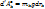 (OZ). Сумма элементарных работ всех сил тяжести равна:
(OZ). Сумма элементарных работ всех сил тяжести равна: 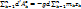 или
или 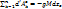 . Тогда полная работа всей системы при переходи из 1 положения во второе = весу всей систем, умноженному на вертикальное перемещение ее центра тяжести.
. Тогда полная работа всей системы при переходи из 1 положения во второе = весу всей систем, умноженному на вертикальное перемещение ее центра тяжести.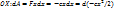 . Полная работа сил упругости будет равна
. Полная работа сил упругости будет равна 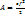 – пропорциональна квадрату перемещения.
– пропорциональна квадрату перемещения.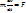 ; умножим обе части на dr:
; умножим обе части на dr: 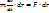 . В правой части стоит элементарная работа; левую часть можно представить:
. В правой части стоит элементарная работа; левую часть можно представить: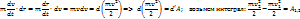
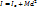 .
.