
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерполяторы. Типы интерполяторов.Содержание книги
Поиск на нашем сайте
20.Аппроксимация нелинейных участков траектории рабочего органа.
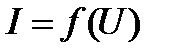 ], или в табличной форме [в виде таблицы координат точек функции ], или в табличной форме [в виде таблицы координат точек функции 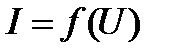 ]. При аналитических методах расчета нелинейных цепей к ВАХ предъявляются требования, чтобы они были представлены в аналитической форме, т.е. в виде аналитического выражения.Под аппроксимацией ВАХ понимают замену ее графической или табличной формы на аналитическую. К уравнению аппроксимации предъявляются два противоречивых требования. Во-первых, уравнение аппроксимации должно по возможности точно описывать заданную ВАХ. Для более полного выполнения этого требования необходимо усложнять структуру этого уравнения. Во-вторых, уравнение аппроксимации, будучи введенным в систему уравнений Кирхгофа, должно позволять решение этой системы доступными методами. Для выполнения этого требования структура этого уравнения должна быть по возможности более простой. Таким образом, при выборе уравнения аппроксимации всегда приходится принимать компромиссное решение между этими двумя требованиями.Различают два способа аппроксимации нелинейных ВАХ – полная и кусочная (по частям).В простейших случаях при монотонном характере изменения функции I (U) ВАХ может быть аппроксимирована полностью одним нелинейным уравнением (рис. 212а). ]. При аналитических методах расчета нелинейных цепей к ВАХ предъявляются требования, чтобы они были представлены в аналитической форме, т.е. в виде аналитического выражения.Под аппроксимацией ВАХ понимают замену ее графической или табличной формы на аналитическую. К уравнению аппроксимации предъявляются два противоречивых требования. Во-первых, уравнение аппроксимации должно по возможности точно описывать заданную ВАХ. Для более полного выполнения этого требования необходимо усложнять структуру этого уравнения. Во-вторых, уравнение аппроксимации, будучи введенным в систему уравнений Кирхгофа, должно позволять решение этой системы доступными методами. Для выполнения этого требования структура этого уравнения должна быть по возможности более простой. Таким образом, при выборе уравнения аппроксимации всегда приходится принимать компромиссное решение между этими двумя требованиями.Различают два способа аппроксимации нелинейных ВАХ – полная и кусочная (по частям).В простейших случаях при монотонном характере изменения функции I (U) ВАХ может быть аппроксимирована полностью одним нелинейным уравнением (рис. 212а).
В более сложных случаях, когда функция I (U) имеет несколько максимумов и минимумов, полная аппроксимация ВАХ одним уравнением становится проблематичной и нерациональной. В таких случаях применяют кусочную аппроксимацию. Суть ее состоит в том, что вся ВАХ разбивается по тому или другому принципу на отдельные участки (куски) (рис. 212б). Отдельные участки аппроксимируются однотипными, но простыми по структуре, уравнениями, коэффициенты в которых изменяются при переходе от одного участка к другому. Если отдельные участки ВАХ аппроксимируются отрезками прямой
Кусочная аппроксимация широко применяется при расчете нелинейных цепей на ЭВМ.
21.Линейный интерполятор по методу оценочной функции (МОФ). Пример. Уравнение отрезка прямой, производимой системой ЧПУ, можно записать в виде. Где xi, yi –точки, лежащие на прямой, а Δx, Δy - приращения xi Δy= yiΔx xi Δy- yiΔx=0 Если это уравнение приравнять к некоторой функции, то получим:
F=xi Δy- yiΔx, из этого уравнения видно, что если функция равно 0, то точка расположена на прямой, если функция больше 0, то точка над прямой, если функция меньше 0, то точка под прямой. Таким образом, оценка функции по уравнению позволяет разработать алгоритм оценочной функции, при котором с определенной частотой анализируется знак оценочной функции. В зависимости от знака выдается единичное приращение по соотв. Координате, масштаб приращения по каждой координате принимается равным дискретности шага этой координате F=yiΔx -xi Δy.
Fi+1=Fi+Δx- выражение для оц. Функции в случае единичного шага по х
- АЛГОРИТМ
Пример – расчет траектории движения рабочего органа по методу оц функции, управляющие импульсы по большей координате выдаются в каждый интервал времени, а импульсы по меньшей координате – в зависимости от значения оценочной функции.
Модифицированный алгоритм линейной интерполяции по МОФ Пример..
Усовершенствованный метод оценочной функции позволяет повысить скорость отработки перемещения, которая в случае траектории под углом 45° может быть повышена в 2 раза. Минимальная скорость подачи определяется по выражению: vмин=h/Tн
h – единичный шаг, определяемый дискретностью системы, Tн – время реализации алгоритма подачи. Требуемая частота импульсов определяется скоростью подачи и углом наклона к осям.
Погрешность расчета траектории по данному методу не превышает дискретности системы ЧПУ
23.Круговая интерполяция по методу оценочной функции. Пример. Применение оценочной функции для круговой интерполяции производится тем же способом, что и для линейной. Xi2+yi2=R2 Fi= xi2+yi2-R2
Знак оценочной функции определяет операцию управления на следующем шаге. Для интерполяции по дуге окружности необходимо знать центр квадранта, координаты начальной и конечной точек, а также радиус дуги окружности. Для воспроизведения дуги окружноcти в 1-м квадранте. F>0 xi+1=xi-1 yi+1=y
Если оценочная функция больше 0, то делается шаг по координате х (по у неизменна) F>0 xi+1=xiyi+1=y+1 После очередного шага осуществляется сравнение текущих координат с конечными и если они не совпадают, то алгоритм повторяется. Определим оценочную функцию после следующего шага по координате х. Fi+1=(xi-1)2+yi2-R2=Fi-2x+1 Определим оценочную функцию после следующего шага по координате y. Yi+1=y+1 xi+1=x Fi+1=xi2+(yi+1)2-R2=Fi+2yi+1
24.Модифицированный алгоритм круговой интерполяции по МОФ. Пример. для повышения контурной скорости можно усовершенствовать алгоритм круговой интерполяции. усовершенствование алгоритма закл в том что как и при линейн. интерполяции по ведущей коорд-те приращения выдаются на каждом шаге.отличие от линейн интерполяции в данн случае закл в следующем:если участок интерполяции в пределах одного квадранта охватывает угол
Введём обозначения
25.Интерполяция на основе цифровых дифференциальных анализаторов пример Интерполяция с использов.ЦДА заключается в моделировании дифуравнений воспроизв.траектории с помощью специальных вычислительных устройств,называемых дифференциальными анализаторами.В данном методе в отличии метода оценочн. ф-иимоделируется не алгебраич. ур-ние а его 1-ая производная или дифф.уравнение.Решение дифуравнений с помощью ЦДА осуществл. путём перехода к разностным ур-ниям с последующим их решением.В связи с чем задача интерполяции по методу ЦДА сводится к следующему:1)Находится обыкновенное дифуравнение,решение которого является уравнение траектории рабочего органа.2)Составляется аналоговая модель для решения данного ур-ния.3)на основе аналоговой модели строится ЦДА, осуществляющий решение ур-ний в цифровом виде(разностном виде). Для интерполяции прямолинейного участка траектории:
Рис а: для линейн интерполят-ра по коорд-те у. В регистр RG запис. знач-е подынтегральн. ф-ии,которая через элем-ты И подаётся на если
26.Интерполяция методом цифрового интегрирования. пример. Метод цифрового интегрирования (МЦИ) заключается в том, что приращения по координатам вычисляются за определённый кварт времени и могут отличаться от единичных. При использовании метода цифрового интегрирования значение i- той координаты и скорость её изменения в момент времени t могут быть вычислены по формулам:
Определение траектории движения формируется путём задания закона изменения ускорения в функции времени Наиболее трудоёмким методом цифрового интегрирования является метод Эйлера:
Реализация круговой интерполяции требует решения ДУ окружности. Для обеспечения требуемой точности требуется использование алгоритмов, которые требуют дополнительных затрат и времени. Поэтому на практике применяются более простые методы приближённого расчёта. Аналогично уравнениям при линейной интерполяции, уравнения для угловой интерполяции будут иметь вид:
Система ЧПУ формирует сигнал задания скорости на привода, которые получаются путём расчёта приращений по координатам
27.Интерполятор на основе интегратора с параллельным переносом. схема
28.Интерполятор на основе интегратора с последовательным переносом Сигнальная диаграмма.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 1450; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.64.131 (0.009 с.) |




 , то такая аппроксимация получила название кусочно-линейной. Если отдельные участки ВАХ аппроксимируются квадратичной (
, то такая аппроксимация получила название кусочно-линейной. Если отдельные участки ВАХ аппроксимируются квадратичной ( ) или кубической (
) или кубической ( ) параболой, то отдельные участки получили название сплайнов, а сама аппроксимация – аппроксимации сплайнами. Кусочная аппроксимация позволяет получить высокую степень приближения к заданной ВАХ, однако требует большого числа однотипных расчетов при определении коэффициентов в уравнениях аппроксимации.
) параболой, то отдельные участки получили название сплайнов, а сама аппроксимация – аппроксимации сплайнами. Кусочная аппроксимация позволяет получить высокую степень приближения к заданной ВАХ, однако требует большого числа однотипных расчетов при определении коэффициентов в уравнениях аппроксимации.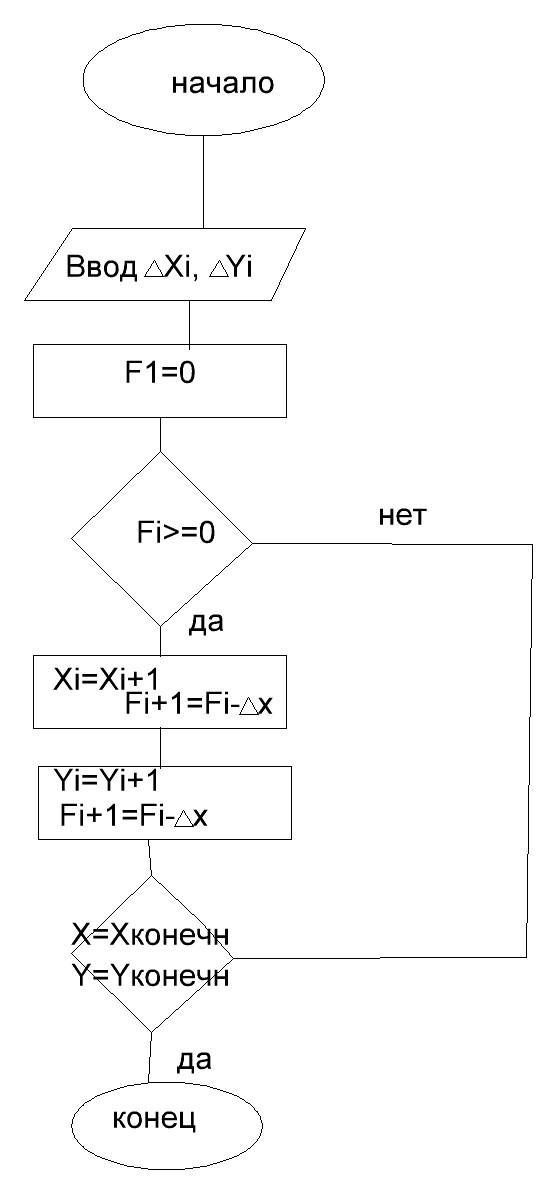 Начало производимого участка совмещается с началом координат и определив знак оценочной функции, выдается шаг по координате x (F>=0) или по координате y (F<0), после чего вновь определяется знак оценочной функции и делается приращение по соотв. Координате. Этот процесс по вторяется до тех пор, пока значение координат и будет соотв. конечной точке участка прямой.
Начало производимого участка совмещается с началом координат и определив знак оценочной функции, выдается шаг по координате x (F>=0) или по координате y (F<0), после чего вновь определяется знак оценочной функции и делается приращение по соотв. Координате. Этот процесс по вторяется до тех пор, пока значение координат и будет соотв. конечной точке участка прямой.



 ,то ведущая координата меняется и это изменение происходит при
,то ведущая координата меняется и это изменение происходит при  .
.
 и для определения ведущей координаты вычислим разность
и для определения ведущей координаты вычислим разность  тогда получим что
тогда получим что  -ведущая координата при (
-ведущая координата при ( )<0,
)<0,  -ведущая координата при (
-ведущая координата при ( ,Таким образом, при
,Таким образом, при  и движении в пределах
и движении в пределах  выдача шагов производится по обеим координатам а при
выдача шагов производится по обеим координатам а при  -только по ведущей координате т е
-только по ведущей координате т е 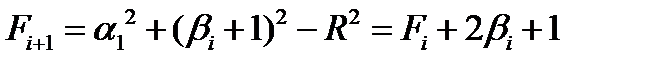 .при
.при  и
и  выдача шагов производится по обеим координатам при
выдача шагов производится по обеим координатам при  -только по ведущей коорд-те т е
-только по ведущей коорд-те т е  .из рисунка видно что при модифицированном алгоритме круговой интерпол-ии по МОФ затрачивается меньше шагов это приводит к увеличению контурной скорости отработки траектории.
.из рисунка видно что при модифицированном алгоритме круговой интерпол-ии по МОФ затрачивается меньше шагов это приводит к увеличению контурной скорости отработки траектории. ,
,  ,
,  -приращение по соответствующим координатам.
-приращение по соответствующим координатам.  (1)для реализации кругового интерполятора запишем уравнение окружности:
(1)для реализации кругового интерполятора запишем уравнение окружности:  ;
;  ;
;  ;Вычисление интеграла в цифровой технике мож.быть выполнено по формулам прямоугольника и трапеции.
;Вычисление интеграла в цифровой технике мож.быть выполнено по формулам прямоугольника и трапеции.  (3)
(3) 
 ;Так как в устр-вах ЧПУ процессы интерполяции и выдачи управляющих команд между собой не связаны,то масштабные множители
;Так как в устр-вах ЧПУ процессы интерполяции и выдачи управляющих команд между собой не связаны,то масштабные множители  принять=1,тогда система(3) будет преобразована к виду:
принять=1,тогда система(3) будет преобразована к виду:  ;так как выходной сигнал интерполят. выдаёт в унитарн. коде,то приращение по координате нулевое или единичное.Ур-ния для трапеции и прямоуг. приобретают вид(*).На основе ур-ния(*) составл. схема интегратора,который может быть реализован параллельн. либо последов. переносом.
;так как выходной сигнал интерполят. выдаёт в унитарн. коде,то приращение по координате нулевое или единичное.Ур-ния для трапеции и прямоуг. приобретают вид(*).На основе ур-ния(*) составл. схема интегратора,который может быть реализован параллельн. либо последов. переносом. 
 ,при этом временные интервалы опред-тся тактовой частотой генератора,который задаёт масштабн. множ-ль
,при этом временные интервалы опред-тся тактовой частотой генератора,который задаёт масштабн. множ-ль  .частота переполнения этих имп-сов прямо пропорц числу
.частота переполнения этих имп-сов прямо пропорц числу  .связь между вых частотой и
.связь между вых частотой и  :
: 
 =
=  ,то приращ-е переменн по коорд-те у будет постоянно,т.е. движ-е будет происх с пост скоростью.Если величина подынтегр ф-ии
,то приращ-е переменн по коорд-те у будет постоянно,т.е. движ-е будет происх с пост скоростью.Если величина подынтегр ф-ии  (5);
(5); 

 .
.
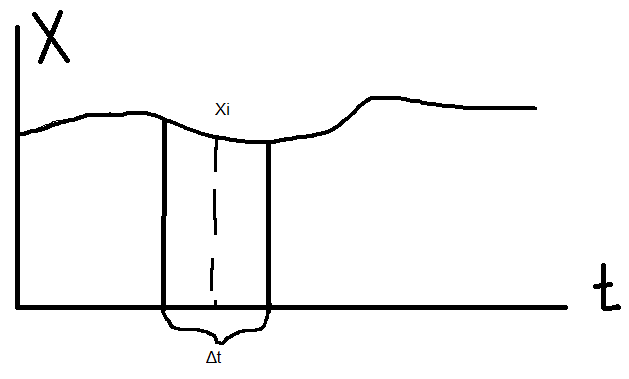
 При реализации линейной интерполяции изменение скорости происходит по следующей диаграмме:
При реализации линейной интерполяции изменение скорости происходит по следующей диаграмме:
 На основании рисунка можно записать следующие выражения:
На основании рисунка можно записать следующие выражения: Вычисление такой системы затруднительно, и поэтому пользуются следующими выражениями:
Вычисление такой системы затруднительно, и поэтому пользуются следующими выражениями:

 C учётом всех преобразований получают выражения в координатах
C учётом всех преобразований получают выражения в координатах  ,
,  :
: :
:






