Группирование и разгруппирование

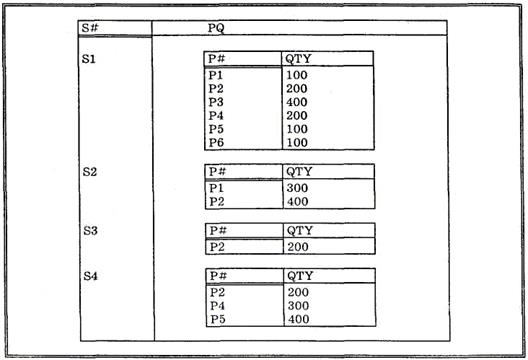
Поскольку значениями атрибутов отношений могут быть другие отношения, было бы желательным наличие дополнительных реляционных операторов, называемых операторами группирования и разгруппирования. Рассмотрим сначала пример операции группирования

SP GROUP (P#, QTY) AS PQ

Результат выполнения этого выражения будет выглядеть так, как показано на рис.12.

 

Рис.13 Группирование отношения SP по атрибуту S#.

Реляционные сравнения

Реляционная алгебра в том виде, в котором она была изначально определена, не поддерживает прямого сравнения двух отношений (например, проверки их равенства или того, является ли одно из них подмножеством другого). Одно из следствий данного упущения состоит в том, что некоторые запросы выражаются весьма неуклюже. Однако это упущение легко исправить. Сначала определим новый вид условия — реляционное сравнение — со следующим синтаксисом.

<реляционное выражение> Θ <реляционное выражение>

Здесь параметр <реляционное выражение> — это в обоих случаях выражения реляционной алгебры, представляющие совместимые по типу отношения, а символ Θ — это один из следующих операторов сравнения.

= Равно

≠ Не равно

≤ Подмножество

< Собственное подмножество

≥ Супермножество

> Собственное супермножество

Реляционное исчисление.

В реляционной модели определяются два базовых механизма манипулирования данными:

· основанная на теории множеств реляционная алгебра

• основанное на математической логике реляционное исчисление.

Также как и выражения реляционной алгебры формулы реляционного исчисления определяются над отношениями реляционных баз данных, и результатом вычисления также является отношение.

Эти механизмы манипулирования данными различаются уровнем процедурности:

• запрос, представленный на языке реляционной алгебры, может быть вычислен на основе вычисления элементарных алгебраических операций с учетом их старшинства и возможных скобок
• формула реляционного исчисления только устанавливает условия, которым должны удовлетворять кортежи результирующего отношения. Поэтому языки реляционного исчисления являются более непроцедурными или декларативными.

Пример: Пусть даны два отношения:

СОТРУДНИКИ (СОТР_НОМЕР, СОТР_ИМЯ, СОТР_ЗАРПЛ, ОТД_НОМЕР)
ОТДЕЛЫ(ОТД_НОМЕР, ОТД_КОЛ, ОТД_НАЧ)

Мы хотим узнать имена и номера сотрудников, являющихся начальниками отделов с количеством работников более 10. Выполнение этого запроса средствами реляционной алгебры распадается на четко определенную последовательность шагов:

(1).выполнить соединение отношений СОТРУДНИКИ и ОТДЕЛЫ по условию СОТР_НОМ = ОТДЕЛ_НАЧ.

С1 = СОТРУДНИКИ [СОТР_НОМ = ОТД_НАЧ] ОТДЕЛЫ

(2).ограничить полученное отношение по условию ОТД_КОЛ > 50

С2 = С1 [ОТД_КОЛ > 50].

(3).спроецировать результаты предыдущей операции на атрибуты СОТР_ИМЯ, СОТР_НОМЕР

С3 = С2 [СОТР_ИМЯ, СОТР_НОМЕР]

Заметим, что порядок выполнения шагов может повлиять на эффективность выполнения запроса. Так, время выполнения приведенного выше запроса можно сократить, если поменять местами этапы (1) и (2). В этом случае сначала из отношения СОТРУДНИКИ будет сделана выборка всех кортежей со значением атрибута ОТДЕЛ_КОЛ > 50, а затем выполнено соединение результирующего отношения с отношением ОТДЕЛЫ. Машинное время экономится за счет того, что в операции соединения участвуют меньшие отношения.

На языке реляционного исчисления данный запрос может быть записан как:

Выдать СОТР_ИМЯ и СОТР_НОМ для СОТРУДНИКИ таких, что

существует ОТДЕЛ с таким же, что и СОТР_НОМ значением ОТД_НАЧ

и значением ОТД_КОЛ большим 50.

Здесь мы указываем лишь характеристики результирующего отношения, но не говорим о способе его формирования. СУБД сама должна решить какие операции и в каком порядке надо выполнить над отношениями СОТРУДНИКИ и ОТДЕЛЫ. Задача оптимизации выполнения запроса в этом случае также ложится на СУБД.

Алгебраическая формулировка является процедурной, т.е. задающей правила выполнения запроса, а логическая - описательной (или декларативной), поскольку она всего лишь описывает свойства желаемого результата. На самом деле эти два механизма эквивалентны и существуют не очень сложные правила преобразования одного формализма в другой.