ГЛАВА 7. Особенности теоретико-множественных операций реляционной алгебры

Объединение

В математике объединением двух множеств называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из исходных множеств. Поскольку отношение является множеством (точнее, содержит множество), а именно — множеством кортежей, очевидно, что можно получить объединение двух таких множеств. Результатом выполнения этой операции будет множество, состоящее из всех кортежей, которые принадлежат хотя бы одному из исходных отношений. Например, объединение множества кортежей описания поставщиков переменной-отношения S и множества кортежей описания деталей переменной-отношения Р, определенно, будет множеством.

Однако, хотя результатом объединения является множество, оно не всегда будет отношением, поскольку в отношении не может быть кортежей разных типов. Нам же требуется, чтобы результатом операции объединения обязательно было отношение, поскольку необходимо соблюдать свойство реляционной замкнутости. Поэтому объединение в реляционной алгебре — это не обычное математическое объединение, а, скорее, специальный вид объединения, требующий, чтобы отношения на входе были совместимы по типу, т.е. чтобы, например, оба отношения содержали кортежи поставщиков или кортежи деталей, но не комбинацию этих типов кортежей. Если два исходных отношения совместимы по типу, то результат их объединения также будет отношением и свойство замкнутости будет сохранено.

Точное определение оператора реляционного объединения. Для заданных отношений А и В одного и того же типа объединением этих двух отношений (что записывается как АUNION В) называется новое отношение того же типа с телом, состоящим из множества всех кортежей t, которые принадлежат либо отношению А, либо отношению В, либо обоим отношениям одновременно.

Пример. Пусть отношения А и В будут такими, как показано на рис.2 (отношение А представляет поставщиков из Лондона, а отношение В — поставщиков, которые поставляют деталь под номером 'Р1'). Тогда выражение A UNION В (см. рис.2,а) представляет поставщиков, которые или находятся в Лондоне, или поставляют деталь под номером 'Р1' (или и то, и другое). Обратите внимание, что результат имеет три кортежа, а не четыре — повторяющиеся кортежи удаляются по определению. Вопрос удаления дубликатов не возникает в других традиционных операциях над множествами, фактически еще существует только одна операция (помимо объединения), где этот вопрос актуален, - операция проекции.

Рис.6. Примеры операций объединения, пересечения и вычитания.

Пересечение

Как и для оператора объединения, для реляционного оператора пересечения (и по тем же причинам) необходимо, чтобы его операнды были совместимы по типу. Итак, п ересечением двух совместимых по типу отношений А и В (что записывается как A INTERSECT В) называется отношение того же типа с телом, состоящим из множества всех кортежей t, которые принадлежат одновременно обоим исходным отношениям А и В.

Пример. Пусть вновь отношения А и В будут такими, как показано на рис.2. Тогда выражение A INTERSECT В (см. рис. 2, б) представляет поставщиков, которые находятся в Лондоне и поставляют деталь под номером 'Р1'.

Вычитание

Как и для операторов объединения и пересечения, для реляционного оператора вычитания необходимо, чтобы его операнды были совместимы по типу. Тогда вычитанием двух совместимых по типу отношений А и В (что записывается как A MINUS В, причем порядок их указания здесь играет роль) называется отношение того же типа, что и отношения А и В с телом, состоящим из множества всех кортежей t, которые принадлежат отношению А, но не принадлежат отношению В.

Пример. Пусть еще раз отношения А и В будут такими, как показано на рис. 2. Тогда выражение A MINUS В (см. рис. 2, в) представляет поставщиков, которые находятся в Лондоне и не поставляют деталь под номером 'Р1', а выражение В MINUS А (см. рис. 2, г) представляет поставщиков, которые поставляют деталь под номером 'Р1' и не находятся в Лондоне. Заметьте, что при вычитании учитывается порядок следования операндов, точно так, как в обычной арифметике (например, 5-2 и 2-5 — это не одно и то же).

Произведение

В математике декартово произведение (или для краткости — просто произведение) двух множеств является множеством всех таких упорядоченных пар элементов, что первый элемент в каждой паре берется из первого множества, а второй элемент в каждой паре берется из второго множества. Следовательно, декартово произведение двух отношений должно быть множеством упорядоченных пар кортежей. Но, опять-таки, необходимо сохранить свойство замкнутости; иначе говоря, результат должен содержать кортежи, а не упорядоченные пары кортежей. Поэтому версия декартова произведения в реляционной алгебре представляет собой расширенную форму операции, в которой каждая упорядоченная пара кортежей заменяется одним кортежем, образованным из двух сцепленных кортежей этой пары. "Сцепление" здесь означает объединение (в смысле теории множеств, а не реляционной алгебры), т.е. кортежи { А1:а1, А2:а2,..., Am:am }и{ В1:b, В2:b2,..., Bn:bn } объединяются в один кортеж. { А1:а1, А2:а2,..., Аm:аm, В1:b1, В2:b2,..., Bn:bn }.

Другая проблема, возникающая в связи с декартовым произведением, заключается в том, что результирующее отношение должно иметь правильно сформированный заголовок. Очевидно, что заголовок результирующего отношения должен содержать все атрибуты из двух исходных отношений. Однако, если эти два заголовка имеют какие-то общие имена атрибутов, возникает проблема. Если допустить подобную операцию, то результирующий заголовок будет иметь два одинаковых атрибута, а значит, будет "неверно сформированным". Поэтому, чтобы построить декартово произведение двух отношений, которые имеют какие-то общие имена атрибутов, необходимо прежде применить оператор RENAME для переименования соответствующих атрибутов.

В результате можно определить (реляционное) декартово произведение двух отношений А и В (что записывается как A TIMES В), где отношения А и В не имеют общих имен атрибутов, как новое отношение с заголовком, представляющим собой объединение заголовков двух исходных отношений А и В, и с телом, состоящим из множества всех кортежей t. таких, что каждый кортеж t представляет собой объединение двух кортежей, один из которых принадлежит отношению А, а другой — отношению В. Кардинальность результата равняется произведению кардинальностей исходных отношений А и В, а степень равняется сумме их степеней.

Пример. Пусть отношения А и В будут такими, как показано на рис. 3 (отношение А представляет, например, номера всех существующих на данный момент поставщиков, а отношение В — номера всех поставляемых на текущий момент деталей). Тогда произведение A TIMES В — это набор всех возможных на текущий момент пар из значений номера поставщика и номера детали.

Рис. 7. Пример операции декартова произведения.

Специальные реляционные операции*

Выборка

Пусть задано отношение А с атрибутами X и Y (, возможно, с другими атрибутами), а символ Θ обозначает любой скалярный оператор сравнения (=, ≠, ≥,< и т.д.), такой, что условие X Θ Y корректно определено и при заданных значениях атрибутов X и Y его проверка дает значение истина или ложь. Тогда Θ-выборкой из отношения А по атрибутам X и Y (что записывается, например, как S WHERE CITY = 'London', причем именно в этом порядке) называется отношение, имеющее тот же заголовок, что и отношение А, и тело, содержащее множество всех кортежей t отношения А, для которых проверка условия X ΘY дает значение истина.

Необходимо отметить следующее:

В выражении WHERE допускаются только единичные операции сравнения. Однако на основании свойства замкнутости можно недвусмысленно расширить определение до такой формы, в которой условие в выражении WHERE будет содержать произвольное число логических сочетаний подобных единичных сравнений благодаря следующим тождествам.

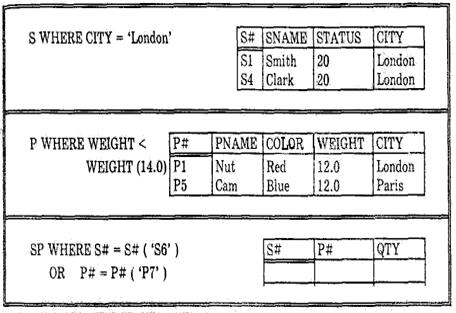
A WHERE c1 AND с2 ≡ (A WHERE c1) INTERSECT (A WHERE с2)

A WHERE c1 OR c2 ≡ (A WHERE c1) UNION (A WHERE c2)

A WHERE NOT c ≡ A MINUS (A WHERE С)

Поэтому впредь будем подразумевать, что параметр < логическое выражение> в предложении WHERE для операции выборки содержит произвольное число логических сочетаний единичных сравнений (с использованием круглых скобок, если необходимо указать желаемый порядок вычисления), где каждое единичное сравнение, в свою очередь, включает либо атрибуты указанного отношения, либо обращение к оператору выборки, либо и то, и другое. Значение параметра <логическое выражение> может быть истолковано как истина или ложь для каждого заданного кортежа в отдельности независимо от остальных. Описанное выше значение параметра < логическое выражение> принято называть условием выборки.

В результате выполнения оператора выборки будет получено "горизонтальное" подмножество заданного отношения, т.е. такое подмножество кортежей заданного отношения, для которого удовлетворяется указанное условие выборки. На рис.4 приводится несколько примеров операции выборки.

 

Рис.8. Примеры операции выборки.

Проекция

Пусть задано отношение А с атрибутами X, Y,..., Z. Тогда проекцией отношения А по атрибутам X, У,..., Z (что записывается как А {X, Y,..., Z }) называется отношение, удовлетворяющее следующим требованиям.

■ Его заголовок получается из заголовка отношения А посредством удаления из него всех атрибутов, не входящих в множество {X, Y,..., Z}.

■ Его тело содержит множество всех кортежей вида {X:x, Y:y,..., Z:z}, таких, для которых в отношении А значение атрибута X равно х, значение атрибута Y равно у,..., значение атрибута Z равно z.

Таким образом, с помощью оператора проекции создается "вертикальное" подмножество заданного отношения, т.е. подмножество, получаемое путем исключения всех атрибутов, не указанных в заданном списке атрибутов, с последующим исключением дублирующихся кортежей (подкортежей) из того, что осталось от исходного отношения.

Из этого определения можно сделать следующие выводы

1. Никакой атрибут не может быть указан в списке атрибутов более одного раза.

2. Если в списке атрибутов указаны все атрибуты отношения А, то такая проекция представляет собой тождественную проекцию.

3. Проекция вида А{ } (т.е. такая, в которой список атрибутов пуст) также допустима.

Она представляет собой нулевую проекцию.

Несколько примеров операции проекции показано на рис.5. В первом примере (проекция отношения поставщиков по атрибуту CITY), несмотря на то, что исходное отношение S имеет пять кортежей (и, следовательно, пять значений городов), в результирующем отношении присутствует только три города, поскольку дублирующиеся кортежи исключены. Аналогичные замечания можно сделать и для других примеров.

 

Рис.9. Примеры операций проекции.

Соединение

Операция соединения имеет несколько разновидностей. Однако наиболее важным, без сомнения, является естественное соединение, причем настолько важным, что общий термин соединение почти всегда используется для обозначения именно естественного соединения. Далее приводится определение.

 

Пусть отношения А и В имеют заголовки

{ XI, Х2,..., Xm, Yl, Y2,..., Yn }

и

{ Yl, Y2,..., Yn, Zl, Z2,..., Zp }

соответственно, т.е. атрибуты Yl, Y2,..., Yn (и только они) — общие для двух этих отношений, XI, Х2,...., Xm — остальные атрибуты отношения А и Zl, Z2,..., Zp - остальные атрибуты отношения В. Далее будем рассматривать выражения {XI, Х2,...,Xm}, {Yl, Y2,..., Yn} и {Zl, Z2,..., Zp} как три составных атрибута X, Y и Z соответственно. Тогда естественным соединением отношений А и В (что записывается как A JOIN В) называется отношение с заголовком {X, Y, Z} и телом, содержащим множество всех кортежей вида {Х:х, Y:y, Z:z}, таких, для которых в отношении А значение атрибута X равно х, а значение атрибута Y равно у и в отношении В значение атрибута Y равно у, а значение атрибута Z равно z

Пример естественного соединения (естественное соединение S JOIN P по общему атрибуту CITY) приведен на рис. 6.

Рис.10. Естественное соединение S JOIN P.

 

Замечание. Соединения необязательно выполняются по внешнему ключу и соответствующему первичному ключу, хотя такие соединения весьма распространены и являются важным частным случаем.

Деление

Определение оператора деления. Пусть отношения А и В имеют заголовки { X1, Х2,..., Хm } и { Yl, Y2,..., Yn } соответственно (т.е. заголовки отношений А и В не пересекаются). Пусть также отношение С имеет следующий заголовок.

{ XI, Х2,..., Xm, Yl, Y2,..., Yn }

(Иначе говоря, заголовок отношения С является объединением заголовков отношений А и В.) Далее будем рассматривать множества { X1, Х2,..., Хm } и { Yl, Y2,, Yn } как составные атрибуты X и Y соответственно. Тогда результатом деления отношения А на отношение B по отношению С (что записывается как A DIVIDEBY В PER С, где отношение А представляет собой делимое, отношение В — делитель, а отношение С — "посредник") называется отношение с заголовком {X} и телом, содержащим множество всех кортежей вида {Х:х}, таких, что кортеж вида {Х:х, Y:y} принадлежит отношению В для всех кортежей вида {Y:y}, принадлежащих отношению В. Нестрого это можно сформулировать так: результат содержит такие Х-значения из отношения А, для которых соответствующие Y-значения из отношения С включают все Y-значения из отношения В.

На рис. 8 показаны некоторые простые примеры операции деления. В каждом случае делимое (отношение DEND) — это проекция текущего, значения переменной-отношения S по атрибуту S#, посредник (MED) — это проекция текущего значения переменной-отношения SP по атрибутам S# и P#, а три делителя (отношения DOR)— такие, как показано на рисунке. В частности рассмотрим последний пример, в котором делителем является отношение, содержащее номера всех известных в данный момент деталей. В результате, получим номера поставщиков, поставляющих все типы этих деталей. Как видно из примера, оператор DIVIDEBY полезен именно для запросов такого рода. Более того, если запрос на обычном языке включает слово "все" ("определить поставщиков всех типов деталей"), то почти наверняка понадобится использовать операцию деления. Тем не менее, следует отметить, что подобны запросы удобнее записывать в терминах реляционных сравнений.