Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналитическая группировка. Признак-фактор и признак-результат. П2Стр 1 из 5Следующая ⇒
Аналитическая группировка. Признак-фактор и признак-результат. П2 Аналитическая группировка служит для выявления зависимости между признаками. При этом выделяют признак-фактор и признак-результат. Группировка осуществляется по признаку-фактору. В каждой группе рассчитывается среднее значение признака-результата. Анализируя изменение средних значений признака-результата от группы к группе, можно сделать вывод о наличии или отсутствии взаимосвязи между признаками. Различие групповых средних позволяет утверждать, что признаки взаимозависимы. Если изменение величины признака-фактора в определенном направлении вызывает изменение признака-результата в том же направлении, то говорят, что связь положительная, а в противном случае − отрицательная.
Проследить зависимость между признаками можно также на основе комбинационной группировки, которая осуществляется одновременно по двум признакам. Если наибольшие числа каждой строки и каждого столбца располагаются вдоль "главной диагонали" таблицы, то можно сделать вывод, что связь положительная и близкая к линейной. Если наибольшие числа располагаются вдоль другой диагонали таблицы, то можно сделать вывод, что связь отрицательная и близкая к линейной. Если числа во всех клетках примерно одинаковые, то связи между признаками нет.
Рядами распределения называются числовые ряды, характеризующие структуру совокупности по некоторому признаку. Ряд распределения может быть получен в результате структурной группировки. Ряд распределения, образованный по количественному признаку (вариационный ряд), может быть дискретным (признак принимает ограниченное число возможных значений, например 2,3,4,5) или интервальным (значения признака выражены вещественными числами или число возможных значений признака достаточно велико). Вариационный ряд оформляется в виде таблицы, где в первой графе указываются варианты (интервалы) значений признака, а в следующих − частота и частость. Ряд распределения в целом характеризует структуру совокупности по данному признаку. Однако могут использоваться и кумулятивные ряды, т.е. ряды накопленных частот (частостей).
Накопленная частота (частость) − это число (доля) элементов совокупности, у которых Накопленная частота на конец i -го интервала определяется по формуле
Вариационный ряд можно изобразить в виде графика. Изображением дискретного ряда является полигон. При его построении по оси абсцисс откладываются варианты (xi), а по оси ординат − частоты или частости − fi. Затем точки с координатами (xi;fi) последовательно соединяются отрезками прямой. Изображением интервального ряда является гистограмма. При ее построении по оси абсцисс откладываются интервалы ряда. Над осью абсцисс строится прямоугольник, основанием которого является интервал, а высотой − значение частоты или частости. Изображением ряда накопленных частот является кумулята. Накопленные частоты откладываются по оси ординат для границ интервалов и соединяются отрезками прямых.
Средняя арифметическая - для не сгруппированных данных для сгруппированных данных где xi − ni − частота i-й группы; k − количество групп. 1. Медиана Ме(x) Медиана представляет собой такое значение признака, которое делит объем совокупности пополам в том смысле, что число элементов совокупности со значениями признака, меньшими медианы, равно числу элементов совокупности со значениями признака, большими медианы. Численное значение медианы можно определить по ряду накопленных частот. Накопленная частота для медианы равна половине объема совокупности:
Для интервального ряда сначала определяется интервал, в котором будет находиться медиана. Само же значение Ме(x) может быть приближенно определено с помощью интерполяции
где x0 − начало интервала, содержащего медиану;
− величина интервала, содержащего медиану; F(x0) − накопленная частота на начало интервала, содержащего медиану; n − объем совокупности; n0 − частота интервала, в котором расположена медиана. 2. Мода Мо(Х) – наиболее часто встречающееся значение признака в совокупности. Для дискретного ряда это то значение признака, которому соответствует наибольшая частота распределения. Для интервального ряда вначале определяется интервал, содержащий моду (с наибольшей частотой). Затем приближенно вычисляется значение моды по формуле
где х0 – начало интервала, содержащего моду; − величина интервала; n0 – частота интервала, в котором расположена мода; n-1 – частота интервала, предшествующего модальному; n1 – частота интервала, следующего за модальным.
Абсолютные показатели · размах вариации:
Относительные показатели · относительный размах вариации (коэффициент осцилляции):
· относительное отклонение по модулю (линейный коэффициент вариации):
· коэффициент вариации:
Сглаживание и выравнивание. Во всяком статистическом распределении неизбежно присутствуют элементы случайности, связанные с тем, что число наблюдений ограничено, что произведены именно те, а не другие опыты, давшие именно те, а не другие результаты. Только при очень большом числе наблюдений эти элементы случайности сглаживаются, и случайное явление обнаруживает в полной мере присущую ему закономерность. На практике мы почти никогда не имеем дела с таким большим числом наблюдений и вынуждены считаться с тем, что любому статистическому распределению свойственны в большей или меньшей мере черты случайности. Поэтому при обработке статистического материала часто приходится решать вопрос о том, как подобрать для данного статистического ряда теоретическую кривую распределения, выражающую лишь существенные черты статистического материала, но не случайности, связанные с недостаточным объемом экспериментальных данных. Такая задача называется задачей выравнивания (сглаживания) статистических рядов. Задача выравнивания заключается в том, чтобы подобрать теоретическую плавную кривую распределения, с той или иной точки зрения наилучшим образом описывающую данное статистическое распределение (рис. 7.5.1).
Задача о наилучшем выравнивании статистических рядов, как и вообще задача о наилучшем аналитическом представлении эмпирических функций, есть задача в значительной мере неопределенная, и решение ее зависит от того, что условиться считать «наилучшим». Например, при сглаживании эмпирических зависимостей очень часто исходят из так называемого принципа или метода наименьших квадратов (см.
Аналогично обстоит дело и с задачей выравнивания статистических рядов. Как правило, принципиальный вид теоретической кривой выбирается заранее из соображений, связанных с существом задачи, а в некоторых случаях просто с внешним видом статистического распределения. Аналитическое выражение выбранной кривой распределения зависит от некоторых параметров; задача выравнивания статистического ряда переходит в задачу рационального выбора тех значений параметров, при которых соответствие между статистическим и теоретическим распределениями оказывается наилучшим.
Метод наименьших квадратов В большинстве экспериментальных данных, задаваемых с помощью табличной функции, имеется достаточно большой разброс точек. При этом использование кусочной или непрерывной интерполяции не всегда оправдано, поскольку ставится задача исследовать общую тенденцию изменения физической величины. В этом общем случае аппроксимации искомая кривая не обязательно должна проходить через заданные точки. Рассмотрим рис. 1, отражающий большой разброс точек. В простейшем случае будем искать аппроксимирующую функцию ф(х) в виде полинома первой степени (прямой):
Рис. 1. Аппроксимация Таким образом, данная система точек группируется вокруг искомой прямой. Эту прямую легко провести на глаз так, чтобы она наиболее близко подходила к исходным точкам. Однако можно найти уравнение прямой более строгими математическими методами. Метод наименьших квадратов наиболе часто используют для решения контрольных по эконометрике для нахождения параметров уравнений (линий, степенной функции, гиперболы и т.д.) Пусть общее количество точек равно n. Отклонение i-й точки от искомой прямой:
Как видно из рис. 2, отклонения могут быть как положительными, так и отрицательными. Поэтому для того, чтобы определить близость искомой функции к табличным точкам, необходимо составить сумму квадратов всех отклонений.
Линейная модель тренда Модуль Обобщенные линейные модели (GLZ) позволяет анализировать как линейные, так и нелинейные эффекты для любого количества и типа предикторов с дискретной или непрерывной зависимой переменной (включая множественную логит, пробит модели, распознавание сигналов и многие другие). Кроме того, в этом модуле реализованы разнообразные типы анализов, такие как биномиальная и множественная логит и пробит регрессия или Теория определения сигнала (SDT).
Модуль GLZ вычислит все стандартные итоговые статистики, включая критерии оценки правдоподобия, статистики Вальда для значимых эффектов, оценки параметров, их стандартные ошибки, доверительные интервалы и т.д. Интерфейс, способы задания плана и использование программы аналогичны модулям GLM, GRM и PLS. Пользователь может легко задать ANOVA или ANCOVA-подобные планы, планы поверхности отклика, смешанные планы и т.д.; поэтому, даже у новичков не возникнет трудностей с применением обобщенных линейных моделей к анализу данных. Кроме того, модуль GLZ предоставляет обширный выбор инструментов проверки модели, таких как таблицы и графики различных статистик остатков или выбросов (включая исходные остатки, остатки Пирсона, сумму квадратов остатков, стьюдентизированные остатки Пирсона, стьюдентизированные суммы квадратов остатков, остатки правдоподобия, дифференциальные статистики Хи-квадрат, дифференциальную сумму квадратов, обобщенные расстояния Кука и т. д. Аналитическая группировка. Признак-фактор и признак-результат. П2 Аналитическая группировка служит для выявления зависимости между признаками. При этом выделяют признак-фактор и признак-результат. Группировка осуществляется по признаку-фактору. В каждой группе рассчитывается среднее значение признака-результата. Анализируя изменение средних значений признака-результата от группы к группе, можно сделать вывод о наличии или отсутствии взаимосвязи между признаками. Различие групповых средних позволяет утверждать, что признаки взаимозависимы. Если изменение величины признака-фактора в определенном направлении вызывает изменение признака-результата в том же направлении, то говорят, что связь положительная, а в противном случае − отрицательная.
Проследить зависимость между признаками можно также на основе комбинационной группировки, которая осуществляется одновременно по двум признакам. Если наибольшие числа каждой строки и каждого столбца располагаются вдоль "главной диагонали" таблицы, то можно сделать вывод, что связь положительная и близкая к линейной. Если наибольшие числа располагаются вдоль другой диагонали таблицы, то можно сделать вывод, что связь отрицательная и близкая к линейной. Если числа во всех клетках примерно одинаковые, то связи между признаками нет.
Рядами распределения называются числовые ряды, характеризующие структуру совокупности по некоторому признаку. Ряд распределения может быть получен в результате структурной группировки. Ряд распределения, образованный по количественному признаку (вариационный ряд), может быть дискретным (признак принимает ограниченное число возможных значений, например 2,3,4,5) или интервальным (значения признака выражены вещественными числами или число возможных значений признака достаточно велико).
Вариационный ряд оформляется в виде таблицы, где в первой графе указываются варианты (интервалы) значений признака, а в следующих − частота и частость. Ряд распределения в целом характеризует структуру совокупности по данному признаку. Однако могут использоваться и кумулятивные ряды, т.е. ряды накопленных частот (частостей). Накопленная частота (частость) − это число (доля) элементов совокупности, у которых Накопленная частота на конец i -го интервала определяется по формуле
Вариационный ряд можно изобразить в виде графика. Изображением дискретного ряда является полигон. При его построении по оси абсцисс откладываются варианты (xi), а по оси ординат − частоты или частости − fi. Затем точки с координатами (xi;fi) последовательно соединяются отрезками прямой. Изображением интервального ряда является гистограмма. При ее построении по оси абсцисс откладываются интервалы ряда. Над осью абсцисс строится прямоугольник, основанием которого является интервал, а высотой − значение частоты или частости. Изображением ряда накопленных частот является кумулята. Накопленные частоты откладываются по оси ординат для границ интервалов и соединяются отрезками прямых.
Средняя арифметическая - для не сгруппированных данных для сгруппированных данных где xi − ni − частота i-й группы; k − количество групп. 1. Медиана Ме(x) Медиана представляет собой такое значение признака, которое делит объем совокупности пополам в том смысле, что число элементов совокупности со значениями признака, меньшими медианы, равно числу элементов совокупности со значениями признака, большими медианы. Численное значение медианы можно определить по ряду накопленных частот. Накопленная частота для медианы равна половине объема совокупности:
Для интервального ряда сначала определяется интервал, в котором будет находиться медиана. Само же значение Ме(x) может быть приближенно определено с помощью интерполяции
где x0 − начало интервала, содержащего медиану; − величина интервала, содержащего медиану; F(x0) − накопленная частота на начало интервала, содержащего медиану; n − объем совокупности; n0 − частота интервала, в котором расположена медиана. 2. Мода Мо(Х) – наиболее часто встречающееся значение признака в совокупности. Для дискретного ряда это то значение признака, которому соответствует наибольшая частота распределения. Для интервального ряда вначале определяется интервал, содержащий моду (с наибольшей частотой). Затем приближенно вычисляется значение моды по формуле
где х0 – начало интервала, содержащего моду; − величина интервала; n0 – частота интервала, в котором расположена мода; n-1 – частота интервала, предшествующего модальному; n1 – частота интервала, следующего за модальным.
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 250; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.223.123 (0.042 с.) |
 значения признака не превышают данного.
значения признака не превышают данного.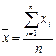 ,
, ,
, варианта или середина интервала i-й группы;
варианта или середина интервала i-й группы; .
. ,
,

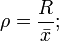
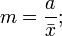
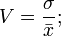

 14.5), считая, что наилучшим приближением к эмпирической зависимости в данном классе функций является такое, при котором сумма квадратов отклонений обращается в минимум. При этом вопрос о том, в каком именно классе функций следует искать наилучшее приближение, решается уже не из математических соображений, а из соображения, связанных с физикой решаемой задачи, с учетом характера полученной эмпирической кривой и степени точности произведенных наблюдений. Часто принципиальный характер функции, выражающей исследуемую зависимость, известен заранее из теоретических соображении, из опыта же требуется получить лишь некоторые численные параметры, входящие в выражение функции; именно эти параметры подбираются с помощью метода наименьших квадратов.
14.5), считая, что наилучшим приближением к эмпирической зависимости в данном классе функций является такое, при котором сумма квадратов отклонений обращается в минимум. При этом вопрос о том, в каком именно классе функций следует искать наилучшее приближение, решается уже не из математических соображений, а из соображения, связанных с физикой решаемой задачи, с учетом характера полученной эмпирической кривой и степени точности произведенных наблюдений. Часто принципиальный характер функции, выражающей исследуемую зависимость, известен заранее из теоретических соображении, из опыта же требуется получить лишь некоторые численные параметры, входящие в выражение функции; именно эти параметры подбираются с помощью метода наименьших квадратов.