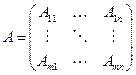Нахождение минимального и максимального элементов массива

Одной из наиболее распространенных задач обработки массивов является поиск минимального (максимального) элемента.

Пример 31.

В массиве X из 20 вещественных чисел поменять местами наибольшие и наименьшие элементы.

Уточним пространство решений. В массиве X может присутствовать несколько максимальных и минимальных элементов. Возможен неординарный случай для этой задачи, который состоит в том, что все элементы массива равны между собой. Переменные, используемые в программе, и их тип описаны в следующей таблице:

Идентификатор	Содержательный смысл	Тип
Х[I]	Элемент с индексом I массива X	REAL
MIN	Значение наименьшего элемента из X	REAL
МАХ	Значение наибольшего элемента из X	REAL

Эту задачу нужно решать с помощью двух последовательных просмотров массива X. Целью первого просмотра является вычисление наибольшего МАХ и наименьшего МIN значений элементов массива X. В начале просмотра значение первого элемента Х[1] считается одновременно наибольшим и наименьшим, что справедливо в том случае, если в массиве всего один элемент. Далее со второго элемента Х[2] и до последнего Х[20] сравниваются значение текущего элемента с MIN. Если значение текущего элемента меньше, то оно с этого момента считается минимальным. По окончании цикла в рабочей ячейке MIN окажется число, равное значению наименьшего элемента. Аналогично поступаем для нахождения МАХ.

Далее нужно сравнить между собой MIN и МАХ. Если эти величины равны между собой, то массив состоит из 20 равнозначных элементов. Следовательно, переставлять их местами нет необходимости. Если MIN≠МАХ, то нужно наименьшим элементам присвоить значение МАХ, а наибольшим элементам присвоить значение MIN. Эти действия являются основой для второго просмотра массива X.

 

PROGRAM PR31;

VAR

X: ARRAY [ 1.. 20] OF REAL;

I: INTEGER;

MIN, MAX: REAL;

BEGIN

WRITELN('Введите массив X, из 20 вещественных чисел');

FOR I:= 1 ТО 20 DO READ(X[I]);

MIN:=Х[1];

МАХ:=Х[1];

FOR I:= 2 ТО 20

DO BEGIN

IF MIN>X[I]

THEN MIN:= X[I];

IF MAX<X[I]

THEN MAX:= X[I];

END;

IF MIN <> MAX

THEN FOR I:= 1 TO 20

DO BEGIN

IF MAX = X[I]

THEN X[I]:= MIN

ELSE IF MIN = X[I]

THEN X[I]:=MAX;

END;

WRITELN('Элементы массива X имеют значения:');

FOR I:= 1 TO 20 DO WRITE(X[I]: 4:1,' ');

WRITELN

END.

 

3.3. Сортировка одномерного массива

Сортировка — перестановка местами объектов в определенном порядке. Известно несколько сотен алгоритмов сортировки и их модификаций.

Пусть дана последовательность элементов – A₁, А₂, …, А_n. Сортировка означает перестановку этих элементов в новом порядке А_k1, А_k2, …, A_kn. Этот порядок соответствует значениям некоторой функции F, такой, что справедливо отношение F(A_k1) < F(A_k2)<... <F(A_kn).

Как у любого вычислительного процесса у сортировки есть свои критерии для сравнительной оценки качества программы и соответствующего ей алгоритма. Такими критериями являются: объем используемой памяти и время работы программы.

Хорошей по критерию памяти считается такая сортировка, при которой данные сортируются в том же самом массиве, где находились исходные данные.

При оценке времени сортировки используют два показателя: число сравнений ключей (С), число пересылок данных (М). Хорошими по времени считаются сортировки, в которых число сравнений С=N*Ln(N). К простым, то есть не очень хорошим, относятся такие сортировки, в которых число сравнений пропорционально квадрату размерности N исходного массива С≈N². Следует отметить, что показатели С и М существенно зависят от первоначальной упорядоченности сортируемого массива. Наиболее тяжелым (Мах) считается случай, когда массив упорядочен в обратном порядке. Ниже мы рассмотрим три наиболее известных способа сортировки одномерного массива. Сравнительные временные характеристики этих способов приведены в следующей таблице:

Способ	Min	Средний	Max
Метод Пузырька	C = (N^2 -N)/2, М = 0	C = (N^2 -N)/2, M = 0.75·(N^2-N)	C = (N^2 -N)/2, M = 1.5· (N^2-N)
Простой выбор	C = (N^2-N)/2, M = 3· (N-1)	C = (N^2 -N)/2, M = N· (Ln(N) + 0.57)	C = (N^2-N)/2, M = N^2/4 + 3· (N-l)
Простое включение	C = N-1, M = 2· (N-1)	C = (N^2+N-2)/4, M = (N^2-9N-10)/4	C = (N^2 -N)/2-l, M = (N^2 +3N-4)/2

Сортировка простым обменом. Метод пузырька

Пример 32.

Методом пузырька упорядочить (отсортировать) в порядке возрастания массив из 8 целых чисел (44, 55, 12, 42, 94, 18, 06, 67).

Концептуальную модель сортировки рассмотрим на примере восьми целых чисел, которые расположим в первом вертикальном столбце. Вертикальное расположение сортируемого массива наглядно иллюстрирует «всплывание легких элементов (чисел) вверх к поверхности» по мере сортировки массива.

Элементы массива рассматриваются попарно снизу-вверх. Если нижний элемент меньше, то они меняются местами. При первом просмотре (проходе) самый «легкий» элемент оказывается самым верхним. Поэтому при втором просмотре его можно уже не рассматривать. В таблице стрелками показаны перемещения элементов массива после каждого прохода.

Индекс элемента массива	Номер прохода сортировки (I)
J=1	44

Элементы всплывают вверх к поверхности в соответствии с их весами, пока не встретят элемент с более малым весом. С каждым проходом наиболее легкий элемент из оставшихся поднимается на свое место, показанное жирными цифрами. Таким образом, нет необходимости на каждом проходе проверять элементы, стоящие выше выделенных, поскольку они уже отсортированы ранее. Начиная с 6 прохода, состояние массива не изменяется, что объясняется начальной упорядоченностью элементов в исходном массиве.

Эта программа предназначена для изучения сортировки методом пузырька, поэтому взят массив из восьми целых чисел. Массив заранее известен, следовательно, инициализировать Х[1...8] проще всего в разделе констант. Ввод данных с клавиатуры в этой программе не требуется. Алгоритм программы представляет собой двойной вложенный цикл. Индекс I внешнего арифметического цикла соответствует номеру прохода сортировки. Индекс J это номер элемента в массиве. Для перестановки двух соседних элементов X[J-1] и X[J] местами используется промежуточная рабочая ячейка с идентификатором L.

 

PROGRAM PR32;

CONST

X: ARRAY [1.. 8] OF INTEGER = (44, 55,12,42,94,18,06, 67);

VAR

L, I, J: INTEGER;

BEGIN

{ Вывод на экран исходного массива X }

FOR I:= 1 ТО 8 DO WRITE(X[I]:5);

WRITELN;

FOR I:= 2 TO 8

DO FOR J:=8 DOWNTO I

DO IF X[J-1] > X[J]

THEN BEGIN{Переставить X[J-1] с Х[J] местами}

L:=X[J-1];

X[J-1]:=X[j];

X[J]:=L

END; {IF}

{ Вывод на экран отсортированного массива X }

FOR I:= 1 ТО 8 DO WRITE(X[I]:5);

WRITELN

END.

 

Сортировка простым включением

Пример 33

Методом простого включения упорядочить (отсортировать) в порядке возрастания массив из 8 целых чисел (44, 55,12,42, 94, 18, 06, 67).

Этот метод используют игроки в карты, перебирая все карты по очереди, начиная со второй и ставя ее на свое место по старшинству среди стоящих левее карт.

PROGRAM PR33;

CONST

X: ARRAY [1.. 8] OF INTEGER = (44, 55,12,42, 94,18,06, 67);

VAR

L, I, J: INTEGER;

BEGIN { Вывод на экран исходного массива X }

FOR I:= 1 ТО 8 DO WRITE(X[I]:5);

WRITELN;

FOR I:=2 TO 8

DO BEGIN

J:= I-1; L:= X[I];

WHILE (J > 0) AND (L < Х[I])

DO BEGIN { Переставить Х[J] на место Х[J+1]}

X[J+1]:=X[J];

J:=J-1;

END;
X[J+1]:=L
END;

{ Вывод на экран отсортированного массива X}

FOR I:= 1 ТО 8 DO WRITE(X[I]:5);

WRITELN

END.

 

Сортировка простым выбором

Пример 34.

Методом простого выбора упорядочить (отсортировать) в порядке возрастания массив из 8 целых чисел (44, 55,12,42, 94,18, 06, 67).

Этот метод более предпочтителен, чем сортировка простым включением. Концептуальная модель этого метода состоит в следующем. Начиная с первой позиции, просматриваются все N элементов и находится номер К наименьшего из элементов. Элемент К ставится на первое место. А элемент, стоявший на втором месте, перемещается на место К. На втором проходе I = 2 первый элемент уже не рассматривается. Рассматриваются оставшиеся N-1 элементы и среди них находится наименьший элемент, имеющий номер К. Этот элемент ставится на второе место, а элемент со второго места смещается на место К.

Этот процесс продолжается до тех пор, пока не будет просмотрен весь массив X, содержащий N элементов.

PROGRAM PR34;

CONST

X: ARRAY [1.. 8] OF INTEGER = (44, 55,12,42,94, 18,06,67);

VAR

K,L, I, J: INTEGER;

BEGIN { Вывод на экран исходного массива X }

FOR I:= 1 ТО 8 DO WRITE(X[I]:5);

WRITELN;

FOR I:= 1 TO 7

DO BEGIN

K:= I;

FOR J:= I + 1 TO 8 { Поиск номера К наименьшего X[I]... Х[К]}

DO IF Х[J] < X[K] THEN К:= J;

{ Переставить Х[K] на место Х[I]}

L:=X[I];

X[I]:= Х[К];

Х[К]:= L;

END;

{ Вывод на экран отсортированного массива X }

FOR I:= 1 ТО 8 DO WRITE(X[I]:5);

WRITELN

END.

 

Из всех примеров нетрудно заметить одно существенное неудобство, связанное с использованием регулярных типов. Оно состоит в том, что необходимо сразу фиксировать число элементов массива. В отдельных случаях заранее не известна размерность массива, подлежащего обработке. Например, может возникнуть необходимость в одном случае отсортировать массив в 20 вещественных чисел, а в другом 100. Поэтому в программу приходится вносить исправления. Здесь помогает понятие константы, описанной в разделе CONST. Достаточно заменить описание N = 20 на N = 30, или N = 100 и больше никаких исправлений в программе не потребуется. Либо использовать переменную N, значение которой вводится либо пользователем с клавиатуры, либо присваивается в программе.

 

3.4. Многомерные массивы

Индексы имеют еще одно свойство — чем больше объем массива, тем менее эффективна с ним работа, поэтому часто используют массивы массивов, то есть с двумя, тремя и более индексами для идентификации элементов. Конструирование многомерных массивов в общем виде выглядит следующим образом:

< имя типа > = ARRAY [тип индекса] OF < тип элементов массива >,

где тип элемента массива в свою очередь — массив, содержащий N-1 индекс. Допустима запись:

< имя типа > = ARRAY[ тип индекса N ] OF ARRAY[ тип индекса N-1 ] OF ARRAY [тип индекса N-2] OF... ARRAY [тип индекса 1]

OF < тип элементов массива >;

Так определен массив от N индексов, то есть N -мерный массив. Это же определение массива может быть сделано в сокращенной форме:

<имя типа > = ARRAY [тип индекса N, тип индекса N-1,..., тип индекса 1 ] OF < тип элементов массива >.

Можно использовать и другие формы определения массива:

< имя типа > = ARRAY [тип индекса N, тип индекса N-1] OF ARRAY [тип индекса N-2,..., тип индекса 1] OF <тип элементов массива>;

Все указанные формы описания типов могут быть приведены как в явном виде в разделе TYPE, так и в неявном в разделе VAR. Обращение к многомерному массиву осуществляется с помощью индексированной переменной вида Х[I1, I2,…, IN], где X — имя массива, а I1, I2,..., IN константы, переменные или выражения, типы которых должны соответствовать типам индексов в определении массива. Указанная форма записи индексированной переменной называется сокращенной и наиболее часто используется. Хорошим стилем программирования считается использование в программе либо сокращенной, либо полной формы описания массивов.

Опишем многомерные массивы, содержащие два индекса. Правила работы с такими массивами полностью распространяются на массивы, имеющие три и более индексов.

Двумерные массивы. Матрицы

Массивы массивов, содержащие два индекса (N = 2), называют двумерными. Если элементами таких массивов являются простые числовые данные, то эти массивы часто называют матрицами.

Обращение к элементам двумерного массива осуществляется с помощью индексированных переменных, например A[I, J]. Здесь А имя массива, а I и J константы, переменные или выражения того же типа, что и типы индексов в объявлении массива. Двумерный массив обычно используют для представления в памяти компьютера матриц:

Связь между элементами матрицы A_jj; I= 1…m; J = 1…n и соответствующими компонентами двумерного массива простая и очевидная A_jj <=> A[I, J].

Объявление и инициализация матрицы

Объявление и инициализация матрицы аналогичны описанным выше способам работы с векторами. То есть в разделе VAR переменным отводится место, а начальное значение этих величин специально не устанавливается. Поэтому после объявления массива необходимо его элементам задать необходимые значения. Используется три способа инициализации двумерного массива.

• Если значения элементов массива определены до начала работы программы, то есть известны на этапе формулировки задания на программирование, то можно использовать следующий способ:

CONST

A: ARRAY [1..5, 1..2] OF REAL = ((0.1, -15.3), (7, 0), (-11.89,4), (-78,11.2), (1,0.01));

При таком объявлении массива в разделе констант, вы заносите в двумерный массив А по порядку А[1,1] = 0.1, А[1,2] = -15.3, А[2, 1] = 7, А[2, 2] = 0,... А[5, 2] - 0.01 вещественные числа, перечисленные в круглых скобках. При этом массив является массивом переменных, то есть в процессе работы программы можно менять содержимое любого элемента матрицы.

• Второй способ применяется в том случае, если исходные данные необходимо внести с клавиатуры в процессе выполнения программы. Так как матрица представляет собой конечный набор однотипных элементов, пронумерованных с помощью двух индексов I и J, то удобно использовать вложенный арифметический цикл (операторы FOR) для ввода значений непосредственно с клавиатуры. При этом можно предложить два приема. Предположим, в вашей программе сделаны объявления:

CONST

M = 3;

N = 4;

VAR

A: ARRAY[ 1.. М, 1.. N] OF REAL;

где M — количество строк, а N — количество столбцов в матрице. Первый способ ввода будет иметь инструкцию:

WRITELN('Введите массив А, из 12 вещественных чисел');

FOR I:= 1 ТО М

DO FOR J:= 1 TO N

DO READ(A[I,J]);

При таком способе оператор может ввести все 12 чисел в форме матрицы.

Через пробел в одну строку вводится четыре числа первой строки и затем нажимается на клавишу Enter. Вторая и третья строки матрицы А вводятся аналогично. На экране монитора остается изображение матрицы в удобочитаемом виде, близком к оригиналу.

Второй способ ввода имеет вид:

FOR I:= 1 ТО М

DO FOR J:=l TO N

DO BEGIN

WRITE('A[', I:1, J:1 ']= ');

READLN(A[I, J])

END;

Этот фрагмент программы позволяет вам вводить число непосредственно за подсказкой компьютера, курсор для ввода стоит через пробел за знаком равенства.

• Третий способ заполнения заключается в прямом присвоении в теле программы значений элементам массива. Например, следующие операторы вложенного арифметического цикла в совокупности с оператором присваивания обеспечивают обнуление всех 12 компонентов массива:

FOR I:= 1 ТО М

DO FOR J:=l TO N

DO A[I,J]:=0;

 

Отображение на экране значений двумерного массива

Если в результате работы вашей программы необходимо значения каждого элемента двумерного массива отобразить на экране монитора, то можно воспользоваться любым из двух способов, описанных ниже. Предположим, в вашей программе сделаны объявления:

CONST

M = 3;

N = 4;

VAR

A: ARRAY[ 1.. М, 1.. N] OF REAL;

Тогда первый способ вывода элементов массива в виде матрицы будет иметь инструкцию:

WRITELN(' Элементы матрицы А имеют значения:');

FOR I:= 1 ТО М

DO BEGIN

FOR J:= 1 ТО N

DO WRITE(A[I, J]: С: D,' '); {Вывод строки}

WRITELN {Переход к новой строке}

END;

В этой инструкции первый оператор WRITELN сообщает пользователю, какую информацию он увидит на экране. Второй оператор WRITE сформирует цепочку (строку) вещественных чисел, разделенных пробелами в формате :С:D. Третий оператор WRITELN переведет курсор на новую строку.

Второй способ обеспечивает вывод значений элементов двумерного массива в столбец, причем каждый из элементов будет идентифицирован парой индексов I и J:

FOR I:= 1 ТО М

DO FOR J:=1 TO N

DO WRITELN('A[', I:1, ',', J:1, '] = ', A[I,J]: C: D);

Пример 35.

Найти сумму двух матриц С = А + В размерностью m х n. Элементы С_i,j искомой матрицы С вычисляются по формулам: С_i,j=А_i,j+B_i,j; i = 1...m; j = 1...n.

Эта задача отличается от предыдущего примера тем, что не известна размерность матриц. Поэтому значения тип необходимо ограничить сверху константами GM = Sup m, GN = Sup n.

Структурограмма:

Ввод размерностей М и N матриц А и В;
Формирование массивов A[l..GM, I..GN] и B[I..GM, 1..GN];
	Для I от 1 до М с шагом 1 делать:
		Для J от I до N с шагом 1 делать:
		C[I, J] = A[I, J] + B[I, J];
Вывод массива C на экран

PROGRAM PR35;

CONST

GM = 8;

GN = 8;

VAR

А, В, C: ARRAY [1.. GM, 1.. GN] OF REAL;

M, N, I, J: INTEGER;

BEGIN

WRITELN('Bвeдите количество строк M и столбцов N матриц A и B');

READLN(M, N);

WRITELN('Введите матрицу А');

FOR I:= 1 ТО М DO FOR J:= 1 ТО N DO READ(A[I, J]);

WRITELN('Введите матрицу В');

FOR I:= 1 TO M DO FOR J:= 1 TO N DO READ(B[I, J]);

FOR I:= 1 TO M { Вычисление матрицы С }

DO FOR J:= 1 TO N

DO C[I,J]:=A[I,J] + B[I,J];

WRITELN('Матрица С имеет вид:');

FOR I:= 1 ТО М

DO BEGIN

FOR J:= 1 TO N DO WRITE(A[I, J]: 5: 2,' ');

WRITELN

END

END.

 

Сортировка двумерного массива

Пример 36.

Задан двумерный массив X из 6 строк и 4 столбцов. Упорядочить массив X по возрастанию элементов дробной части столбца с номером N. Отсортированный массив X вывести на экран монитора.

За основу алгоритма возьмем алгоритм сортировки одномерного массива методом пузырька. Отличие этой задачи в том, что переставлять местами нужно не два соседних элемента одномерного массива, а две соседние строки двумерного массива. Перестановка двух строк реализована с помощью арифметического цикла, третьего уровня вложения, с параметром цикла К.

 

 

Структурограмма

Формирование массива X[l..6, 1..4]; Ввод номера столбца N;
	Для I от 2 до 6 с шагом 1 делать:
	Для J от 6 с шагом -1 до I делать:
		FRAC(X[J-1,N]) > FRAC(X[J, N]) True
			Для К от 1 до 4 с шагом 1 делать: { Перестановка строк }
			R = Х[J-1, К]; Х[J-1, K] = Х[J, К]; X[J, К] = R;
Вывод массива X на экран монитора.

PROGRAM PR36;

VAR

X: ARRAY [1..6, 1..4] OF REAL;

N, К, I, J: INTEGER;

R: REAL;

BEGIN

WRITELN('Введите матрицу X');

FOR I:= 1 ТО 6

DO FORJ:= 1 TO 4

DO READ(X[I, J]);

WRITELN('Укажите номер столбца N матрицы X');

READLN(N);

FOR I:=2 TO 6

DO FOR J:=6 DOWNTO I

DO IF FRAC(X[J-1,N])>FRAC(X[J,N])

THEN FOR К:= 1 TO 4 { Перестановка строк}

DO BEGIN

R:= X[J-1, К];

Х[J-1, K]:= X[J, К];

Х[J, K]:- R;

END;

{ Вывод на экран отсортированного массива X }

WRITELN('Матрица X имеет вид:');

FOR I:= 1 ТО 6

DO BEGIN

FOR J:= 1 ТО 4

DO WRITE(X[I, J]: 6: 3,' ');

WRITELN

END

END.