Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача о закреплении самолетов за воздушными линиямиСодержание книги
Поиск на нашем сайте
Эта задача возникает при выборе оптимального варианта плана закрепления самолетов за данными воздушными линиями, обеспечивающего необходимые объемы перевозок при минимальных суммарных эксплуатационных расходах. Пусть имеется n различных типов самолетов, которые нужно распределить между m авиалиниями. Пусть месячный объем перевозок самолетом i-го типа на j-й авиалинии равен аij единицам, а связанные с этим месячные эксплуатационные расходы составляют cij рублей. Определить число xij самолетов i-го типа, которое следует закрепить за j-й авиалинией для обеспечения перевозки по этой линии аij единиц (i= Математическая модель задачи выглядит следующим образом. Целевая функция имеет вид:
ЦФ представляет суммарные эксплуатационные расходы в месяц. Ограничения имеют вид:
xij³ 0, xij- целые числа, i= Условия (1) определяют, что самолеты j-й авиалинии должны обеспечивать объем перевозок не меньше заданного. Условия (2) представляют собой ограничение по количеству имеющихся самолетов i-го типа. Данная задача является задачей целочисленного линейного программирования. Задача о ранце Здесь речь идет о собравшемся в поход путешественнике, который должен упаковать в ранец различные полезные предметы n наименований, причем могут потребоваться несколько одинаковых предметов. Имеются m ограничений такого типа, как вес, объем, линейные размеры и т.д. Пусть аij- i-я характеристика предмета j-го наименования i= Математическая модель задачи выглядит следующим образом. Целевая функция имеет вид:
ЦФ представляет суммарная полезность собранных предметов. Ограничения имеют вид:
xj³ 0, xj- целое, j= Условия (1) означают, что количество отобранных предметов не превышает возможностей погрузки. Данная задача является задачей линейного целочисленного программирования. Задача о назначениях Имеется n работников, которых требуется назначить на n работ. Известно, что j-ю работу i-й работник будет выполнять с эффективностью cij. Требуется так распределить работников, чтобы максимизировать суммарную эффективность. Положим xij=1, если i-й работник назначен на j-ю работу; xij=0, в противном случае, i, j= Математическая модель задачи выглядит следующим образом. Целевая функция имеет вид:
ЦФ представляет суммарную эффективность. Ограничения имеют вид:
xij равно либо 0, либо 1. Условия (1) означают, что каждый работник назначается только на одну работу. Условия (2) означают, что один работник выполняет только одну работу. Данная задача является задачей линейного булева программирования. Задача коммивояжера Имеется n городов. Выезжая из исходного города А1, коммивояжер должен побывать во всех остальных городах по одному разу и вернуться в город А1. Задача заключается в определении последовательности объезда городов при которой коммивояжеру требуется минимизировать некоторый критерий эффективности: стоимость проезда, время в пути, суммарное расстояние и т.д. Пусть задана матрица C=||cij|| расстояний между городами и требуется минимизировать суммарную длину пути. Введем переменные xij=1, если коммивояжер переезжает из города Аi в город Аj, i¹ j; xij=0, в противном случае, i, j= Математическая модель задачи выглядит следующим образом. Целевая функция имеет вид:
ЦФ представляет суммарную длину пути. Ограничения имеют вид:
ui-uj+(n-1)× xij £ n-2, 2£ i¹ j £ n, (3) где ui, i= Условия (1) означает, что коммивояжер выезжает из каждого города один раз, а условия (2)- что он въезжает один раз в каждый город. Условия (3), выглядящие несколько искусственно, предназначены обеспечить связность маршрута коммивояжера. Более точно эти условия запрещают любой цикл, не проходящий через город 1, и тем самым исключают ситуации, подобные приведенной на рисунке.
Данная задача является задачей линейного булева программирования. 1.10. Задача о доставке (покрытии множества) Фирма обслуживает некоторое количество клиентов (m). Каждый день она доставляет своим клиентам товары на грузовых машинах (или по железной дороге, воздушным путем, на баржах и т.д.). Существует множество допустимых маршрутов (n) доставки, каждый из которых позволяет обслужить определенное подмножество клиентов и требует использования в течении дня одного транспортного средства. Каждый маршрут характеризуется определенными расходами, которые могут соответствовать его длине, или стоимости расходуемого топлива и т.д. Цель состоит в том, чтобы выбрать такое множество маршрутов, при котором обеспечивается обслуживание каждого из клиентов, каждый клиент обслуживается один раз в день и суммарные расходы минимальны. Введем переменные: xj=1, если маршрут j выбран; xj=0, в противном случае, j= Обозначим элементы aij следующим образом: aij=1, если i-й клиент обслуживается по маршруту j; aij=0, в противном случае, i= Обозначим стоимость доставки по маршруту j через сj. Математическая модель задачи выглядит следующим образом. Целевая функция имеет вид:
ЦФ представляет суммарные расходы доставки по выбранным маршрутам. Ограничения имеют вид:
Согласно условиям (1) каждый клиент обслуживается один раз в день. Данная задача является задачей линейного булева программирования. Основы работы в Excel Общие сведения об Excel При вызове Excel на экране появится окно, показанное на рис. 1.
Рис. 1 Основными элементами окна являются: главное меню; панель инструментов; строка формул (в ней вводятся формулы и значения); строка состояния (здесь отображается информация о состоянии системы, а также контекстные подсказки); поле имени; лист рабочей книги (электронная таблица)- основное рабочее место; ярлычок листа; блок прокрутки листов; угловой элемент, предназначенный для выделения всех ячеек листа; полосы и стрелки прокрутки. В самом начале следует отметить, что иногда удобным оказывается использование Справки, поэтому не рекомендуется пренебрегать помощью, которая в Excel является контекстно зависимой. При возникновении проблем можно нажимать кнопку Справка или клавишу <F1>. Microsoft Excel работает с объектами. Файл Excel (с расширением.xls) является объектом самого высокого уровня и называется рабочей книгой (book). Рабочая книга содержит рабочие листы- объекты. Рабочий лист имеет вид таблицы, которая состоит из строк, пронумерованных числами, и столбцов, озаглавленных буквами. В одной электронной таблице (рабочем листе) 16394 строки и 256 столбцов (A, B,..., AA, AB,....). На пересечении строки и столбца находится ячейка. Ячейка является частью огромной таблицы, но она же одновременно представляет собой самостоятельный объект, с которым можно осуществлять различные операции. Каждая ячейка имеет свой адрес, который состоит из имени столбца и номера строки. При работе с таблицей каждую ячейку идентифицируют по ее адресу. Указание адреса ячейки называют ссылкой, например запись G5 означает ссылку на ячейку, расположенную на пересечении столбца G и строки 5. Ячейка- это контейнер, содержащий информацию, он никогда не бывает пустым. Незаполненная ячейка на экране выглядит пустой, на самом деле в ней, по умолчанию, хранится число 0. Что еще может содержаться в ячейке? В качестве информации может выступать значение какого-либо типа (числовое, текстовое, логическое, дата), а также формула. Возможность ввода в ячейку вычисляемых формул, оперирующих другими ячейками, является главным удобством электронных таблиц вообще и Excel в частности, и придает им особую специфику. Обычная математическая формула состоит из операндов - чисел, переменных, функций, над которыми выполняются операции- умножение, сложение и т.д. В Excel роль операндов выполняют ячейки, а точнее те значения, которые в них хранятся. Требуемое значение можно получить, указав адрес ячейки. Следует отметить, что при построении формулы можно ссылаться на ячейку, также содержащую формулу, при этом операции будут производиться с соответствующим значением формулы, на которую сослались. Главным помощником в работе с Excel является мышь. С ее помощью вы подаете команды для Excel: выбираете опцию меню, нажимаете кнопку на панели инструментов, выделяете область и т.д. В основном при командовании используется левая кнопка мыши, далее в тексте фразы "щелкнуть мышью", "щелкнуть кнопкой мыши" и т.д. подразумевают нажатие именно левой кнопки, в случае, когда необходимо использование правой кнопки мыши этот факт будет указываться. При вводе команд предпочтительнее работать мышью, но иногда удобно использовать клавиатуру, в этом случае ввод осуществляется либо клавишей <Enter> либо комбинацией клавиш, которые по этой причине называются "горячими". Ввод команд осуществляется с помощью меню или кнопок на панели инструментов (см. рис. 1). Все панели делятся на поставляемые (стандартные) и создаваемые пользователем. Настроить те и другие можно выбирая последовательно опции меню Вид, Панели инструментов. Команды бывают двух видов - иерархические и контекстные. В группу иерархических входят команды трех типов:
Нижним уровнем некоторых видов иерархических команд являются диалоговые окна (рис. 2).
Рис. 2 В диалоговых окнах вводятся необходимые параметры и команды. Диалоговые окна имеют достаточно разнообразную структуру, но вместе с тем в них используются одни и те же типовые элементы. Например ярлычки (Страница, Поля, Колонтитулы, Лист), поля ввода, куда вводится запрашиваемая информация, поля выбора (флажки и переключатели), в которых производится выбор команд из числа имеющихся. При этом команды делятся на совместимые и альтернативные. Совместимыми называются такие команды, при которых ввод одной из них не исключает ввода других. Левее таких команд имеется квадратик (флажок). При одном щелчке мыши в квадратике появляется крестик (флажок установлен), которая обозначает ввод данной команды, а ее отсутствие (флажок сброшен)- отмену команды. Альтернативными называются такие команды, для которых назначение одной исключает назначение остальных. Левее этих команд находится кружок (переключатель). После щелчка мыши в кружке либо появляется точка, что означает выбор команды (переключатель выбран), либо убирается, что означает ее отмену. Контекстные команды - это команды, которые инициируются в контексте конкретной сложившейся ситуации. Например, если выделить мышью ярлычок рабочего листа и щелкнуть правой кнопкой, то появится меню, которое будет содержать перечень опций - контекстных команд, таких как Вставка..., Удалить..., Переименовать... и т.д. (они же являются вызывающими диалоговое окно).
|
||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 311; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.158.84 (0.009 с.) |

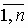 , j=
, j=  ) при минимальных суммарных эксплуатационных расходах, если известно, что имеется Ni самолетов i-го типа (i=
) при минимальных суммарных эксплуатационных расходах, если известно, что имеется Ni самолетов i-го типа (i=  ® min.
® min. ³ aj, j=
³ aj, j=  =Ni, i=
=Ni, i=  ® max.
® max. i=
i=  ® max.
® max. , j=
, j=  , i=
, i= 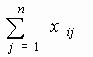 ® min.
® min.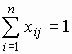 , j=
, j=  - неограниченные действительные переменные.
- неограниченные действительные переменные.
 =1, i=
=1, i=