
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расщепление спектральных линий, не обладающих тонкой структурой, в слабом магнитном поле называется эффектомСодержание книги
Поиск на нашем сайте
а. Зеемана б. Комптона в. Пашена – Бака г. Штарка
152. Закон Мозли посвящен исследованию: а. Спектров атома водорода б. Характеристических рентгеновских спектров в. Гамма излучения г. a - излучения
153. В какой области спектра расположена серия Бальмера в атоме водорода: а. В инфракрасной б. В видимой в. В ультрафиолетовой г. В рентгеновской 154. В какой области спектра расположена серия Бальмера в водородоподобном атоме гелия: а. В рентгеновской б. В инфракрасной в. В видимой г. В ультрафиолетовой
155. Какой переход разрешен правилами отбора: а. 2p3/2 ® 1s1/2 б. 4р5/2 ® 3p3/2 в. 3d5/2 ® 1p1/2 г. 4d5/2 ® 4p1/2
156. При туннельном эффекте энергия микрочастиц: а. Понижается по экспоненциальному закону б. Понижается линейно в. Не изменяется
157. При туннельном эффекте вероятность прохождения микрочастиц сквозь барьер при увеличении толщины барьера: а. понижается по экспоненциальному закону б. понижается линейно в. повышается линейно г. не зависит от толщины барьера 158. Коэффициент прозрачности потенциального барьера определяет: а. отношение квадратов амплитуд падающей волны к прошедшей б. отношение квадратов амплитуд прошедшей волны к падающей в. отношение квадратов амплитуд отраженной волны к падающей г. отношение квадратов амплитуд падающей волны к отраженной 159. При туннельном эффекте максимальной вероятностью прохождения сквозь потенциальный барьер одной и той же высоты и толщины имеет следующая микрочастица (обладают одной энергией): а. a - частица б. Протон в. Нейтрон г. Электрон 160. В опыте Франка и Герца впервые доказано: а. наличие волновых свойств у электронов б. наличие спина у электронов в. дискретность энергетических уровней в атомах г. существование теплового излучения нагретых тел 161. В K оболочке атома может находиться: а. 2 электрона б. 8 электронов в. 18 электронов г. 32 электрона 162. В L оболочке атома может находиться: а. 2 электрона б. 8 электронов в. 18 электронов г. 32 электрона 163. В M оболочке атома может находиться: а. 2 электрона б. 8 электронов в. 18 электронов г. 32 электрона 164. Электронная конфигурация атома 1s22s22p63s. Тогда порядковый номер Z этого атома равен: а. 8 б. 10 в. 11 г. 13 165. Электронная конфигурация атома 1s22s2. Тогда порядковый номер Z этого атома равен: а. 3 б. 4 в. 5 г. 6 166. Электронная конфигурация атома 1s22s22p63s2. Тогда порядковый номер Z этого атома равен: а. 8 б. 10 в. 11 г. 12 167. Порядковый номер магния Z = 12. Тогда его электронная конфигурация: а. 1s22s22p6 б. 1s22s22p63s в. 1s22s22p63s2 г. 1s22s22p63s23р2 168. Порядковый номер фосфора Z = 15. Тогда его электронная конфигурация: а. 1s22s22p63s2 б. 1s22s22p63s23р в. 1s22s22p63s23р2 г. 1s22s22p63s23р3 169. Порядковый номер азота Z = 7. Тогда его электронная конфигурация: а. 1s22s22p б. 1s22s22p2 в. 1s22s22p3 г. 1s22s22p4 170. Порядковый номер алюминия Z = 13. Тогда его электронная конфигурация: а. 1s22s22p33s23p4 б. 1s22p63s23p в. 1s21р22s22p63р г. 1s22s22p63s23р
171. Порядковый номер аргона Z = 18. Тогда его электронная конфигурация: а. 1s21p22s22p63р6 б. 1s22s22p63s23р6 в. 1s22s21p62s21р6 г. 1s22s23p64s25р6 172. Если L – орбитальное, S – спиновое, а J - число, определяющее результирующий механический момент многоэлектронного атома, то в случае L = 2, S = 1 возможные значения J: а. 3, 2, 1 б. -3, -2, -1, 0, 1, 2, 3 в. только 3 г. только 1 173. Если L – орбитальное, S – спиновое, а J - число, определяющее результирующий механический момент многоэлектронного атома, то в случае L = 2, S = 3/2 возможные значения J: а. только 7/2 б. только 1/2 в. 7/2, 5/2, 3/2, 1/2 г. -7/2, -5/2, -3/2, -1/2, 1/2, 3/2, 5/2, 7/2 174. Множитель Ланде имеет отношение к: а. спиновому моменту микрочастицы б. магнитному моменту микрочастицы в. механическому моменту микрочастицы г. орбиральному моменту микрочастицы
175. Множитель Ланде g определяется как а. 0 б. 1/2 в. 1 г. невозможно определить из-за недостаточности данных
176. Множитель Ланде g определяется как а. 2 б. 1 в. 1/2 г. невозможно определить из-за недостаточности данных 177. Множитель Ланде g определяется как а. 0 б. 1/2 в. 3/2 г. 2 178. Множитель Ланде g может принимать: а. только значения, большие или равные 2 б. только значения, большие или равные 1 в. только значения, большие или равные 0 г. и отрицательные, и положительные значения 179. Проекция магнитного момента атома на ось z определяется по формуле а. 0, …, J-1, J б. –J, -J+1,…, J-1, J в. 1/2 и -1/2 г. только J 180. Если обозначить магнетон Бора через mБ, спиновое квантовое число через S, то спиновый магнитный момент электрона mS определяется по формуле: а. б. в. г. 181. Если обозначить магнетон Бора через mБ, спиновое квантовое число через S, то спиновый магнитный момент электрона mS определяется по формуле: а. б. в. г. 182. Если обозначить магнетон Бора через mБ, спиновое квантовое число через S, то спиновый магнитный момент электрона mS определяется по формуле: а. б. в. г. верного ответа нет 183. Если обозначить магнетон Бора через mБ, орбитальное квантовое число через L, то орбитальный магнитный момент электрона mL определяется по формуле: а. б. в. г. 184. Если обозначить магнетон Бора через mБ, орбитальное квантовое число через L, то орбитальный магнитный момент электрона mL определяется по формуле: а. б. в. г. 185. Проекция спина электрона Msz на выделенное направление может принимать следующие значения: а. 1/2 б. ±1/2 в. ±(1/2) г. верного ответа нет 186. Спиновое квантовое число электрона s принимает следующие значения: а. 1/2 б. ±1/2 в. ±(1/2) г. верного ответа нет 187. Если орбитальное квантовое число L = 3, то величина орбитального момента ML (в единицах а. б. 3 в. 1, 2, 3 г. 188. Если орбитальное квантовое число L = 4, то проекция (проекции) орбитального момента MLz (в единицах а. б. 0, 1, 2, 3, 4 в. -4, -3, -2, -1, 0, 1, 2, 3, 4 г. 189. Если орбитальное квантовое число L = 1, то величина орбитального момента ML (в единицах а. 1 б. в. 2 г. 190. Если орбитальное квантовое число L = 3, то проекция (проекции) орбитального момента MLz (в единицах а. б. 0, 1, 2, 3 в. г. -3, -2, -1, 0, 1, 2, 3 191. Электрон, находящийся в d-состоянии, обладает орбитальным моментом ML (в единицах а. б. 3 в. г. 6 192. Результирующий спин S 2-х электронов, находящихся в s-состоянии атома гелия равен: а. 1/2 б. 2 в. 1 г. 0 193. При облучении вещества жестким монохроматическим рентгеновским излучением обнаружено, что максимальная кинетическая энергия комптоновских электронов Т = 0,44 Мэв. Длина волны падающего излучения равна а. 0,01 Å б. 0,02 Å в. 0,04 Å г. 0,08 Å
194. Фотон с энергией 374 кэВ испытал рассеяние на покоившемся свободном электроне. Если комптоновское смещение длины волны равно 0,012 Å, то угол между направлениями разлета электрона отдачи и рассеянного фотона равен а. 60° б. 90° в. 105° г. 155°
|
||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 337; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.86.246 (0.009 с.) |

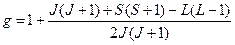 . Тогда в случае, если S = 0, то g равно:
. Тогда в случае, если S = 0, то g равно: (mБ – магнетон Бора, g – множитель Ланде, mJ – квантовое число, определяющее проекции магнитного момента на выделенное направление, - квантовое число, определяющее полный механический момент атома). Число mJ может принимать следующие значения:
(mБ – магнетон Бора, g – множитель Ланде, mJ – квантовое число, определяющее проекции магнитного момента на выделенное направление, - квантовое число, определяющее полный механический момент атома). Число mJ может принимать следующие значения:






















