
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи нечеткой классификации
Пусть имеется набор Заметим, что нечеткое отношение
Это отношение является
из которой следует, в частности, что для любых
Это предельное отношение является конечным результатом обработки результатов нечетких измерений Для произвольного числа
Нетрудно показать, что для любого (1) (2) (3) Заметим, что (3) есть следствие того, что предельное нечеткое отношение
Окончательный этап алгоритма классификации — разбиение множества Выбор величины порога
Порядки и слабые порядки Антисимметричное, транзитивное нечеткое отношение Различные порядки отличаются друг от друга требованиями, предъявляемыми к условию транзитивности. Слабейшее из этих требований — условие ацикличности отношения строгого порядка Если для отношения сходства условие транзитивности обычно записывают в виде
где Ацикличность:
Слабая транзитивность:
Отрицательная транзитивность:
(
(
(
Сильная транзитивность:
Сверхсильная транзитивность:
Метрическая транзитивность:
Квазисерийность:
Ультраметрическая транзитивность:
В общем случае предполагается, что рассмотренные условия транзитивности определены для
Условия ацикличности, слабой транзитивности и отрицательной транзитивности нечеткого отношения
Аналогичные свойства могут быть определены как В отличие от первых трех свойств, остальные свойства более специфичны для нечетких отношений и в большей мере учитывают согласованность силы отношения между элементами множества Частным случаем сильного порядка (порядка, удовлетворяющего условию сильной транзитивности) является метрический порядок. Для асимметричных отношений условие метрической транзитивности эквивалентно неравенству треугольника. Условие квазисерийности определяет нечеткую квазисерию. Каждый
Поскольку обычная квазисерия определяет разбиение множества Частным случаем метрических порядков, помимо квазисерии, является линейный порядок, определяемый условием линейной транзитивности. Линейный порядок при интерпретации Ультраметрическая транзитивность построена по аналогии с метрической транзитивностью, однако для антисимметричныхотношений она не эквивалентна ультраметрическому неравенству Между строгими порядками (асимметричными отношениями) и слабыми порядками (рефлексивными отношениями) существует тесная связь. Эти порядки могут быть получены друг из друга с помощью ряда преобразований. Если на
то на множестве нечетких отношений может быть задана операция дополнения следующим образом:
и на множестве нечетких отношений будут выполняться тождества
Если на множестве нечетких отношений задана операция дополнения, то из отношения строгого порядка Отношение сходства Отношение различия Отношение слабого порядка Транзитивностью отношения Нечеткие отношения порядка могут быть получены многими способами и допускают различную интерпретацию. Они могут выражать либо значение какого-либо физического параметра, характеризующего интенсивность доминирования
|
||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 429; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.156.80 (0.025 с.) |
 фотографических портретов всех членов нескольких семей. Требуется разделить этот набор на группы так, чтобы в каждой оказались портреты членов только одной семьи. Пусть
фотографических портретов всех членов нескольких семей. Требуется разделить этот набор на группы так, чтобы в каждой оказались портреты членов только одной семьи. Пусть  — функция принадлежности нечеткого бинарного отношения сходства на заданном наборе фотографий. Для каждой пары фотографий
— функция принадлежности нечеткого бинарного отношения сходства на заданном наборе фотографий. Для каждой пары фотографий  и
и  значение
значение  -шаговое отношение
-шаговое отношение 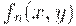 следующим образом:
следующим образом:
 выполняется цепочка неравенств
выполняется цепочка неравенств
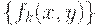 имеет предел при
имеет предел при  . Таким образом, существует предельное отношение сходства, определяемое равенством
. Таким образом, существует предельное отношение сходства, определяемое равенством
 (
( ) вводится обычное (не нечеткое) отношение
) вводится обычное (не нечеткое) отношение  :
:
 — рефлексивность,
— рефлексивность, — симметричность,
— симметричность,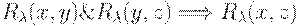 — транзитивность.
— транзитивность. обладает свойством нечеткой транзитивности
обладает свойством нечеткой транзитивности
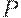 называется отношением упорядочения или порядком. Мы будем рассматривать только строгие порядки, т.е. порядки, для которых выполняется свойство антирефлексивности. Свойства нестрогих (рефлексивных)порядков во многом совпадают со свойствами строгих порядков.
называется отношением упорядочения или порядком. Мы будем рассматривать только строгие порядки, т.е. порядки, для которых выполняется свойство антирефлексивности. Свойства нестрогих (рефлексивных)порядков во многом совпадают со свойствами строгих порядков. и различные способы определения операции композиции позволяют задавать разные типы транзитивности, причем оказывается, что таких типов существует не так уж и много, то для отношения порядка условие транзитивности нечеткого отношения удобно записывать в виде, аналогичном условию транзитивности обычных порядков:
и различные способы определения операции композиции позволяют задавать разные типы транзитивности, причем оказывается, что таких типов существует не так уж и много, то для отношения порядка условие транзитивности нечеткого отношения удобно записывать в виде, аналогичном условию транзитивности обычных порядков:
 — некоторая операция в
— некоторая операция в  . Оказывается, что из множества всех отношений порядка можно выделить значительное количество отличающихся друг от друга классов порядков специального вида, определяемых как способом задания операции
. Оказывается, что из множества всех отношений порядка можно выделить значительное количество отличающихся друг от друга классов порядков специального вида, определяемых как способом задания операции  , если
, если  .
.


 )- транзитивность:
)- транзитивность:
 )- транзитивность:
)- транзитивность:
 )- транзитивность:
)- транзитивность:





 , хотя некоторые условия могут быть обобщены и на случай, когда
, хотя некоторые условия могут быть обобщены и на случай, когда  , определяемого следующим образом:
, определяемого следующим образом:
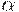 -свойства для различных
-свойства для различных  отношения
отношения 
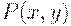 как силы предпочтения альтернативы
как силы предпочтения альтернативы  .
.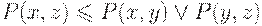 .
. , что на
, что на 





 и
и 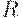 . В частности, если
. В частности, если 


