
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
О методах построения функций принадлежности нечетких множеств
В приведенных выше примерах использованы прямые методы, когда эксперт либо просто задает для каждого х ϵ Е значение μА(х), либо определяет функцию совместимости. Как правило, прямые методы задания функции принадлежности используются для измеримых понятий, таких как скорость, время, расстояние, давление, температура и т.д., или когда выделяются полярные значения. Во многих задачах при характеристике объекта можно выделить набор признаков и для каждого из них определить полярные значения, соответствующие значениям функции принадлежности, 0 или 1. Например, в задаче распознавания лиц можно выделить шкалы, приведенные в табл. 1.1. Таблица 1.1. Шкалы в задаче распознавания лиц
Для конкретного лица А эксперт, исходя из приведенной шкалы, задает μA(х) ϵ [0, 1], формируя векторную функцию принадлежности { μA (х1), μA (х2),…, μA(х9) }. При прямых методах используются также групповые прямые методы, когда, например, группе экспертов предъявляют конкретное лицо и каждый должен дать один из двух ответов: «этот человек лысый» или «этот человек не лысый», тогда количество утвердительных ответов, деленное на общее число экспертов, дает значение μ лысый (данного лица). (В этом примере можно действовать через функцию совместимости, но тогда придется считать число волосинок на голове у каждого из предъявленных эксперту лиц.) Косвенные методы определения значений функции принадлежности используются в случаях, когда нет элементарных измеримых свойств, через которые определяется интересующее нас нечеткое множество. Как правило, это методы попарных сравнений. Если бы значения функций принадлежности были нам известны, например, μA(хi) = ωi, i = 1, 2,..., n,то попарные сравнения можно представить матрицей отношений А = { aij}, где aij = ωi/ωj (операция деления). На практике эксперт сам формирует матрицу А, при этом предполагается, что диагональные элементы равны 1, а для элементов симметричных относительно диагонали aij= 1/aij, т.е. если один элемент оценивается в α раз сильнее, чем другой, то этот последний должен быть в 1/α раз сильнее, чем первый. В общем случае задача сводится к поиску вектора ω, удовлетворяющего уравнению вида Aw = λmax w, где λmax— наибольшее собственное значение матрицы А. Поскольку матрица А положительна по построению, решение данной задачи существует и является положительным.
Можно отметить еще два подхода: · использование типовых форм кривых для задания функций принадлежности (в форме (L-R)-Типа – см. ниже) с уточнением их параметров в соответствии с данными эксперимента; · использование относительных частот по данным эксперимента в качестве значений принадлежности. Операции над нечеткими множествами Логические операции Включение. Пусть А и В — нечеткие множества на универсальном множестве Е. Говорят, что А содержится в В, если Обозначение: А ⊂ В. Иногда используют термин доминирование, т.е. в случае, когда А ⊂ В, говорят, что В доминирует А. Равенство. А и В равны, если Обозначение: А = В. Дополнение. Пусть М = [0, 1], А и В – нечеткие множества, заданные на Е. А и В дополняют друг друга, если Обозначение: Очевидно, что Пересечение. А ⋂ В — наибольшее нечеткое подмножество, содержащееся одновременно в А и В:
Объединение.A ∪ В — наименьшее нечеткое подмножество, включающее как А, так и В, с функцией принадлежности:
Разность.
Дизъюнктивная сумма А ⊕ В = (A - B) ∪ (B - A) = (A ⋂ ̅B) ∪ (̅A ⋂ B) с функцией принадлежности:
Примеры. Пусть
Здесь: 1) А ⊂ В, т. е. А содержится в B или B доминирует А С несравнимо ни с A, ни с В, т.е. пары { А, С } и { А, С } — пары недоминируемых нечетких множеств. 2) A ≠ B ≠ C 3) ̅A = 0,6/ x 1 + 0,8/ x 2 + 1/ x 3 + 0/ x 4; ̅B = 0,3/ x 1 + 0,1/ x 2 + 0,9/ x 3 +0/ x 4. 4) А ⋂ В = 0,4/ x 1+ 0,2/ x 2+ 0/ x 3+ 1 / х 4. 5) A ∪ В = 0,7/x1 + 0,9/ x 2+ 0,1/ x 3+ 1/ x 4. 6) А - В = А ⋂ ̅В = 0,3/ x 1+ 0,l/ x 2+ 0/ x 3+ 0/ x 4; В- А= ̅А ⋂ В= 0,6/ x 1+ 0,8/ x 2+ 0,l/ x 3+ 0/ x 4.
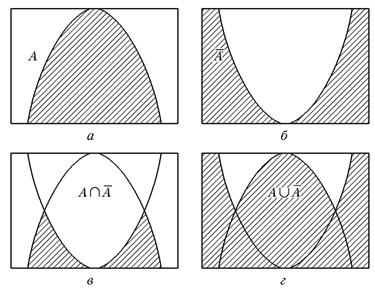
7) А ⊕ В = 0,6/ x 1+ 0,8/ x 2+ 0,1/ x 3+ 0/ x 4. Наглядное представление логических операций над нечеткими множествами. Для нечетких множеств можно строить визуальное представление. Рассмотрим прямоугольную систему координат, на оси ординат которой откладываются значения μА(х), на оси абсцисс в произвольном порядке расположены элементы Е (мы уже использовали такое представление в примерах нечетких множеств). Если Е по своей природе упорядочено, то этот порядок желательно сохранить в расположении элементов на оси абсцисс. Такое представление делает наглядными простые логические операции над нечеткими множествами (см. рис. 1.3).
Рис. 1.3. Графическая интерпретация логических операций: На рис. 1.3α заштрихованная часть соответствует нечеткому множеству А и, если говорить точно, изображает область значений А и всех нечетких множеств, содержащихся в А. На рис. 1.3 б, в, г даны ̅ А, А ⋂ ̅A,A U ̅А. Свойства операций ∪ и ⋂ Пусть А, В, С — нечеткие множества, тогда выполняются следующие свойства:
В отличие от четких множеств, для нечетких множеств в общем случае: A ⋂ ̅A ≠ ∅, A ∪ ̅A ≠ E (что, в частности, проиллюстрировано выше в примере наглядного представления нечетких множеств). Замечание. Введенные выше операции над нечеткими множествами основаны на использовании операций maxи min. В теории нечетких множеств разрабатываются вопросы построения обобщенных, параметризованных операторов пересечения, объединения и дополнения, позволяющих учесть разнообразные смысловые оттенки соответствующих им связок «и», «или», «не». Треугольные нормы и конормы Один из подходов к операторам пересечения и объединения заключается в их определении в классе треугольных норм и конорм. Треугольной нормой(t-нормой) называется бинарная операция (двуместная действительная функция)
удовлетворяющая следующим условиям: 1. Ограниченность: 2. Монотонность: 3. Коммутативность: 4. Ассоциативность:
Примеры треугольных норм min(μA,μB) произведение μA·μB max(0, μA+μB - 1). Треугольной конормой (сокращенно
удовлетворяющая следующим условиям: 1. Ограниченность: 2. Монотонность: 3. Коммутативность: 4. Ассоциативность: Треугольная конорма Она называется строгой, если функция Примеры t-конорм max(μA,μB) μA+ μB- μA· μB min(1, μA+μB). Примерами треугольных конорм являются следующие операторы:
Треугольная норма T и треугольная конорма S называются дополнительными бинарными операциями, если T (a, b) + S (1 − a,1 − b) = 1 для Наибольшей популярностью в теории Заде пользуются три пары дополнительных треугольных норм и конорм. 1) Пересечение и объединение по Заде: TZ (a, b) = min{ a, b }, SZ (a, b) = max{ a, b }. 2) Пересечение и объединение по Лукасевичу:
3) Вероятностное пересечение и объединение:
Операторы дополнения В теории нечетких множеств оператор дополнения не является единственным.
Помимо общеизвестного
существует целый набор операторов дополнения нечеткого множества. Пусть задано некоторое отображение
Это отображение будет называться оператором отрицания в теории нечетких множеств, если выполняются следующие условия: (1) (2) Если кроме этого выполняются условия: (3) (4) то она называется строгим отрицанием. Функция (5) Приведем примеры функции отрицания: Классическое отрицание: Квадратичное отрицание: Отрицание Сугено: Дополнение порогового типа: Будем называть любое значение
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 701; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.196.87 (0.047 с.) |
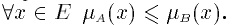
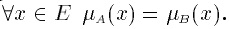


 (дополнение определено для М = [0, 1], но очевидно, что его можно определить для любого упорядоченного М).
(дополнение определено для М = [0, 1], но очевидно, что его можно определить для любого упорядоченного М).

 с функцией принадлежности:
с функцией принадлежности: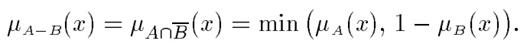





 .
. .
. .
. .
. -конормой) называется двухместная действительная функция
-конормой) называется двухместная действительная функция ,
,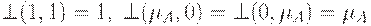 .
. .
. .
. .
. является архимедовой, если она непрерывна
является архимедовой, если она непрерывна выполнено неравенство
выполнено неравенство  .
.
 .
. .
.
 ,
, .
.

 — строго убывающая функция
— строго убывающая функция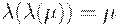 .
. .
. .
. .
. .
.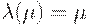 , равновесной точкой. Для любого непрерывного отрицания существует единственная равновесная точка.
, равновесной точкой. Для любого непрерывного отрицания существует единственная равновесная точка.


