
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчетно-графическая работа №1. Решение вычислительных задач с помощью табличного процессора MS ExcelСодержание книги
Поиск на нашем сайте ИНФОРМАТИКА Методические указания к расчетно-графическим работам для студентов всех специальностей всех форм обучения
Алматы 2008 СОСТАВИТЕЛИ: Н.В. Сябина, М.Д.Ешпанова, А.А.Аманбаев. Информатика. Методические указания к расчетно-графическим работам для студентов всех специальностей всех форм обучения. – Алматы: АИЭС, 2008.- 43 с.
Для контроля знаний, полученных студентами в результате самостоятельной работы, в курсе Информатики предусмотрены расчетно-графические работы. Настоящие методические указания включают варианты заданий, рекомендации к их выполнению и контрольные вопросы по трем темам: а) решение вычислительных задач с помощью табличного процессора MS Excel; б) использование возможностей программирования для решения вычислительных задач; в) создание базы данных в среде MS Access. В приложениях содержится весь необходимый для выполнения работ справочный материал. Методические указания предназначены для студентов всех специальностей всех форм обучения. Ил. 2, табл. 20, библиогр. – 25 назв.
Рецензент: канд. тех. наук, доц. Имангалиев Ш.И.
Печатается по плану издания некоммерческого акционерного общества «Алматинский институт энергетики и связи» на 2008 г.
© НАО «Алматинский институт энергетики и связи», 2008 г.
Введение
Как показывает практика, объем аудиторных часов, выделенный на изучение дисциплины «Информатика», не позволяет полностью охватить весь необходимый студентам материал, поэтому некоторые разделы вынесены на самостоятельное изучение. Самостоятельная работа студента (СРС) предполагает не только проработку материала лекций, подготовку к практическим и лабораторным занятиям, но также изучение дополнительного материала. Для проверки знаний, полученных в результате самостоятельной работы студента, в курсе «Информатика» предусмотрены расчетно-графические работы. Настоящие методические указания включают варианты заданий, рекомендации к их выполнению и контрольные вопросы по темам: а) решение вычислительных задач с помощью табличного процессора MS Excel; б) использование возможностей программирования для решения вычислительных задач; в) создание базы данных в среде MS Access. В приложениях содержится весь необходимый для выполнения работ справочный материал. В качестве дополнительного источника информации для выполнения контрольных работ следует использовать учебники, учебные пособия, методические разработки. Кроме того, информацию можно почерпнуть из периодических изданий по компьютерным технологиям, справочной литературы по различным программным продуктам, справочной системы каждой программы, имеющейся в памяти компьютера, а также, используя справочную систему Интернет. Расчетно-графические работы должны быть предоставлены для проверки в электронном виде в сроки, установленные учебной частью. К каждой расчетно-графической работе необходимо приложить пояснительную записку, выполненную в электронном виде (в формате MS Word) или на листах формата А4, включающую титульный лист (приводится в Приложении А), постановку задачи и все необходимые пояснения. При оформлении пояснительной записки рекомендуется использовать шрифт Times New Roman, кегль 12 – 14, выравнивание по ширине страницы, а также допускается применение доступных средств форматирования текстовых документов. Варианты заданий выбираются в соответствии с рекомендациями преподавателя или по схеме: а) определить две последние цифры номера зачетной книжки Nзк; б) если 1£Nзк£25, то номер варианта Nвар=Nзк (так, Nзк=18, Nвар=18); в) если 26£Nзк£99, то Nвар определяется как остаток от деления Nзк на 25. Например, Nзк=78, тогда 78/25=3 (в остатке 3), значит Nвар=3; г) если остаток от деления Nзк на 25 равен 0, то выполняется вариант 25. В случае, если работа содержит ошибки или выполненные задания не соответствуют выбранному варианту, она возвращается студенту для внесения исправлений. Задание на расчетно-графическую работу 2.1.1 Используя методику перевода чисел (таблица В.1), а также ресурсы MS Excel: - создать таблицу перевода заданного числа (таблица Б.1) из десятичной системы счисления в предлагаемую систему счисления (двоичную, восьмеричную или шестнадцатеричную); - создать таблицу обратного перевода полученного результата в десятичную систему. Выполнить те же действия, используя встроенную функцию из категории Инженерные (подключить Пакет анализа). Объяснить возможные ошибки; - с помощью специальной функции из категории Математические перевести заданное число (таблица Б.1) из десятичной системы счисления в римскую систему счисления и обратно; - используя функции MS Excel, выполнить указанную арифметическую операцию над заданными в десятичной системе счисления числами a и b (таблица Б.1), а также перевести исходные числа в римскую систему счисления и получить тот же результат. Рекомендации к выполнению задания. При создании таблиц перевода целесообразно использовать функции ЦЕЛОЕ и ОСТАТ из категории Математические. При переводе в шестнадцатеричную систему (при замене чисел на буквы) рекомендуется использовать вложенную функцию ЕСЛИ, редактируя строку формул. 2.1.2 Используя функцию преобразования из категории Инженерные, составить таблицу перевода данных из одних единиц измерения (таблица Б.2) в другие. Рекомендации к выполнению задания. Полный список единиц измерения, которые могут быть преобразованы, содержится в таблице В.2. Список используемых с метрическими единицами измерений префиксов приведен в таблице В.3. Названия единиц и префиксы учитывают регистр ввода. 2.1.3 Построить график функции (таблица Б.3). Рекомендации к выполнению задания. Для построения графика по предложенным функциям целесообразно использовать тип диаграммы Точечная. 2.1.4 Имеется резервуар с емкостью V, рабочим объемом Vr, объем жидкости в резервуаре Vg. Резервуар в основании имеет круг радиусом r или прямоугольник со сторонами а и b и высоту заполнения h (таблица Б.4). Как только объем жидкости станет превышать рабочий объем резервуара, оператору необходимо отправить сообщение, используя логическую функцию ЕСЛИ. Сообщение «перекрыть клапан» должно быть написано на красном фоне, в противном случае, должно быть выведено сообщение – «не требуется». Используя условное форматирование, проиллюстрировать заполнение резервуара. 2.1.5 Решить систему уравнений (таблица Б.5) методом обратной матрицы и методом Крамера. Рекомендации к выполнению задания. Для решения системы линейных уравнений методом обратной матрицы следует: - записать уравнение в матричной форме (матрица коэффициентов, умноженная на вектор неизвестных, равняется известному вектору правой части); - вычислить определитель матрицы. Для вычисления определителя матрицы в Excel используется функция массива МОПРЕД из категории Математические. Операция вычисления определителя имеет смысл только для квадратных матриц. Если определитель не равен нулю, то решение существует, если определитель равен нулю, то обратной матрицы не существует; - обратить матрицу коэффициентов. Обращение квадратной матрицы производится с помощью функции массива МОБР из категории Математические. При этом процедура обращения матрицы сводится к следующим действиям: а) ввести матрицу; б) указать место, для размещения обратной матрицы, и ее размер (он совпадает с размером исходной матрицы); в) использовать функцию массива МОБР, указав ячейки, в которых находится исходная матрица. Для ввода матричной функции во все ячейки, отмеченные при выборе места обратной матрицы, следует нажать комбинацию клавиш Ctrl+Shift+Enter; - умножить правую часть уравнения на матрицу, обратную матрице коэффициентов. При решении системы методом Крамера можно использовать функцию МОПРЕД из категории Математические. 2.1.6 Используя функции MS Excel, выполнить с заданным массивом (таблица Б.6) следующие действия: - транспонировать исходный массив, результат отобразить в другом диапазоне ячеек; - перемножить исходный и транспонированный массивы; - найти позицию элемента равного заданному числу А. Рекомендации к выполнению задания. При транспонировании, перемножении массивов и поиске искомого элемента следует использовать функции ТРАНСП и ПОИСКПОЗ из категории Ссылки и массивы и МУМНОЖ из категории Математические. Следует учесть, что, если результатом вычислений является массив, то для его отображения на экране необходимо при нажатии кнопки ОК одновременно удерживать клавиши Ctrl+Shift. В противном случае результат будет выведен в виде скалярной величины. 2.1.7 Определить некоторые основные характеристики потоков различных жидкостей: а) вода течет по трубе с внутренним диаметром D (таблица Б.7). Средняя скорость потока равна v. Вычислить площадь поперечного сечения трубы б) на практике широко применяется правило: средняя скорость легкоподвижных жидкостей (вязкость которых по порядку величины совпадает с вязкостью воды) в трубе не должна превышать 1м/с. Определите минимальный диаметр трубы, по которой должно поступать 6000 м3 воды в день при соблюдении сформулированного правила; в) число Рейнольдса определяется соотношением 2.1.8 Резисторный датчик температуры – это прибор, в котором для измерения температуры используется металлическая проволока или пластинка. Электрическое сопротивление металла зависит от температуры, поэтому температуру можно вычислить на основе измерений сопротивления металла. Уравнение, связывающее температуру и сопротивление, имеет вид:
где Rt - сопротивление при измеряемой температуре Т; R0 – сопротивление при температуре 0°С; a - линейный температурный коэффициент. Для платины a = 0,00385 Ом/°С. Вычислить (таблица Б.8): а) сопротивление платинового терморезистора в заданном интервале температур (T1; T2) с указанным шагом hT при известном сопротивлении R0; б) температуру, при которой сопротивление терморезистора равно заданным значениям R(T1; T2) с указанным шагом hR. 2.1.9 Сформировать предложенную таблицу (таблица Б.9), заполнить не менее 10 записей и выполнить выборку данных по различным критериям (три простых запроса с помощью автофильтрации и три сложных запроса с использованием расширенного фильтра). 2.1.10 Сформировать заданные основную и вспомогательную таблицы (таблица Б.10). Выполнить в основной таблице все необходимые вычисления, используя данные вспомогательной таблицы. Рекомендации к выполнению задания. При выполнении вычислений, следует использовать функции просмотра и ссылок ВПР и ГРП из категории Ссылки и массивы, которыепозволяют просматривать и обрабатывать информацию, хранящуюся в прямоугольных таблицах. Все задания следует выполнить в одной рабочей книге MS Excel на отдельных листах.
2.2 Общие рекомендации к выполнению расчетно-графической работы 2.2.1 Системы счисления Для перевода чисел из одной системы счисления в другую разработаны специальные алгоритмы. В таблице В.1 рассматриваются алгоритмы перевода целых положительных чисел. Простота этих алгоритмов позволяет программистам быстро и компактно записывать двоичные числа в восьмеричной и шестнадцатеричной системах, поэтому они часто употребляются в разных современных приложениях (например, для обозначения цвета, адреса ячейки памяти и т.д.). Числа в разных системах счисления формируются по одному и тому же принципу: если использован последний допустимый символ, то в младшем разряде пишут 0, а в старшем 1 (таблица В.4). 2.2.2 Формулы и стандартные функции MS Excel Для создания простой формулы нужно выполнить следующие действия: - щелкнуть в ячейку, в которую требуется ввести формулу; - ввести знак равенства(=); - ввести формулу и нажать клавишу Enter. Формулы вычисляют значения в определенном порядке. Формула вычисляется слева направо, в соответствии с определенным порядком для каждого оператора в формуле. Если в одной формуле используется несколько операторов, MS Excel выполняет операции в следующем порядке: - операторы ссылок (адресные) «:», «,», «»; - знаковый минус «-»; - вычисление процента %; - арифметические ^, *, /, +, -; - текстовый оператор &; - операторы сравнения =, <, >, <=, >=, <>. Если формула содержит операторы с одинаковым приоритетом - например, операторы деления и умножения — они выполняются слева направо. Для того, чтобы изменить порядок выполнения, следует заключить часть формулы, которая должна выполняться первой, в скобки. Структура функции начинается со знака равенства (=), за ним следует имя функции, открывающая скобка, список аргументов, разделенных запятыми, закрывающая скобка. Аргумент - значения, используемые функцией для выполнения операций или вычислений. Существуют различные типы аргументов: число, текст, логическое значение (ИСТИНА и ЛОЖЬ), массивы, значение ошибки (например, #Н/Д) или ссылки на ячейку. Тип аргумента, используемого функцией, зависит от конкретной функции. Для появления списка доступных функций нужно щелкнуть в ячейку и нажать клавиши Shift+F3. Всплывающие подсказки с синтаксисом и аргументами появляются только для встроенных функций после ввода. Диалоговое окно Мастер функций (меню Вставка, команда Функция) облегчает ввод функций при создании формул, содержащих функции. При вводе функции в формулу окно отображает имя функции, все ее аргументы, описание функции, текущий результат функции и всей формулы. Для того, чтобы начать формулу с функции, нужно щелкнуть в ячейку, в которую требуется ввести формулу, после чего: - нажать кнопку Вставка функции на панели формул; - выбрать функцию, которую нужно использовать (можно ввести запрос с описанием операции, которую требуется выполнить, в поле Поиск функции (например, по словам «сложение чисел» будет найдена функция СУММ, или выбрать категорию в поле или категорию); - ввести аргументы (для ввода ссылок на ячейки в качестве аргументов, нужно нажать кнопку свертывания диалогового окна, чтобы временно скрыть его, выделить ячейки на листе и нажать кнопку развертывания диалогового окна); - по завершении ввода формулы нажать клавишу Enter. В некоторых случаях может потребоваться использование функции как одного из аргументов другой функции – вложенной функции. В формулах можно использовать до семи уровней вложения функций. Для создания формулы с вложением функций нужно щелкнуть в ячейку, в которую требуется ввести формулу, и выполнить следующие действия: - нажать кнопку Поместить функцию на панели формул; - выбрать функцию, которую нужно использовать; - ввести в соответствующее окно аргумента другую функцию, в качестве аргумента. Для создания ссылки следует выделить ячейку, диапазон ячеек, место в другом листе или место в другой книге. Можно переместить границу выделения, перетащив границу ячейки, или перетащить угол границы, чтобы расширить выделение. Чтобы создать ссылку на именованный диапазон, нужно нажать клавишу F3, выбрать имя в поле Вставка имени и нажать кнопку ОК. Для того, чтобы создать ссылку на другой лист в той же книге перед ссылкой на диапазон ячеек необходимо поставить имя листа и восклицательный знак (!). Ссылки на ячейки можно ввести в формулу, выделив ячейки непосредственно на листе. Выделение ячеек на листе вставляет абсолютные ссылки. Если необходимо, чтобы ссылки для каждой ячейки в выделенном диапазоне были согласованы, следует использовать относительные ссылки. Одну и ту же формулу можно ввести сразу в несколько ячеек. Для этого, необходимо выделить ячейки, ввести формулу, а затем нажать клавиши Ctrl+Enter. Рассмотрим пример вычисления скалярного произведения векторов а=(-2,-3,1) и b=(0,1,4), а также проверим их ортогональность. Решение (рисунок 2.1). Скалярное произведение векторов а=(x1,y1,z1) и b=(x2,y2,z2) вычисляется по формуле а*b=х1*х2+у1*у2+z1*z2. Если а*b=0, то векторы - ортогональны. Шаг 1. Вводим в подготовленную таблицу исходные данные в ячейки B2:С4. Шаг 2. В ячейку D2 вводим формулу =B2*C2 и нажимаем Enter. Шаг 3. Маркер заполнения протягиваем вниз до ячейки D4. Шаг 4. Выделяем ячейки D2:D4, щелкаем на знак Автосуммы на панели инструментов и в ячейке D5 вычисляем скалярное произведение векторов. Шаг 5. Поскольку значение скалярного произведения не равно 0, делаем вывод, что векторы не ортогональны.
Рисунок 2.1 – Пример вычисления скалярного произведения векторов 2.2.3 Дополнительные возможности MS Excel: надстройка Пакет анализа В MS Excel имеется три типа программ-надстроек: собственно надстройки MS Excel, дополнительные надстройки для модели компонентных объектов (COM) и автоматизированные надстройки. При загрузке надстройки обеспечиваемые ею возможности становятся доступными в MS Excel и в соответствующие меню добавляются все связанные с ними команды. Доступ к автоматизированным надстройкам, зарегистрированным в системе, можно получить через меню Сервис. Надстройка Пакет анализа предоставляет в распоряжение пользователя набор инструментов для анализа данных, полезных при проведении сложного статистического или инженерного анализа. Чтобы выполнить анализ данных с помощью этих инструментов, следует указать входные данные и выбрать параметры; анализ будет выполнен с помощью подходящей статистической или инженерной макрофункции, а результат будет помещен в выходной диапазон. Некоторые функции являются встроенными, другие доступны только после установки пакета анализа. Например, функция ПРЕОБР из категории Инженерные, которая позволяет преобразовать число из одной системы мер в другую, становится доступна только после подключения Пакета анализа. Если данная функция недоступна или возвращает ошибку #ИМЯ?, следует установить и загрузить надстройку Пакет анализа, для этого нужно: - в меню Сервис выбрать команду Надстройки; - в списке надстроек установить флажок на Пакет анализа и нажать ОК; - если необходимо, выполнить инструкции программы установки. Для экономии памяти и повышения производительности следует выгружать надстройки, которые используются редко. Для этого достаточно в списке надстроек (меню Сервис, команда Надстройки) снять флажок с соответствующей надстройки. При выгрузке надстройки ее возможности и соответствующие команды удаляются из MS Excel, однако файл надстройки остается на компьютере и может быть загружен снова. При выгрузке надстройки она остается в памяти до перезапуска MS Excel. 2.2.4 Форматирование ячеек по заданным условиям Одним из способов контроля результатов формулы или других значений является форматирование с применением условных форматов. Для этого, выделив весь диапазон, в меню Формат следует выбрать команду Условное форматирование. Если значение ячейки изменилось и больше не удовлетворяет заданному условию, MS Excel удаляет форматирование из ячейки, но сохраняет условие, так что форматирование будет снова автоматически применено, если значение ячейки удовлетворит условию. Значения выделенных ячеек можно сравнивать с константой или с результатами вычислений по формуле. Чтобы определить условие форматирования при оценке данных в ячейках, не входящих в выделенный диапазон, или при проверке нескольких критериев, можно использовать логическую формулу. Чтобы при выбранном параметре Значение сравнить значения выделенных ячеек с результатом формулы, формула должна начинаться со знака равенства (=). Если был выбран параметр Формула, то указанная формула должна принимать значения ИСТИНА (1) или ЛОЖЬ (0). Формула также должна начинаться со знака равенства (=). Вычисления по данной формуле могут производиться только на активном листе. При вводе формулы в диалоговом окне Условное форматирование (меню Формат, команда Условное форматирование) рекомендуется вводить ссылку только на активную ячейку в выделенном диапазоне. MS Excel устанавливает ссылки для других ячеек относительно активной. 2.2.5 Построение диаграмм Для построения диаграммы следует выделить любую ячейку из тех, что содержат исходные данные диаграммы. Затем выполнить команду Диаграмма меню Вставка или нажать кнопку Мастер диаграмм на стандартной панели инструментов. С помощью окон диалога мастер диаграмм соберет всю необходимую информацию для построения диаграммы. Чтобы построить диаграмму, не прибегая к помощи мастера диаграмм, следует выделить ячейку с исходными данными и нажать клавишу F11. Используя установки по умолчанию, MS Excel создаст диаграмму на отдельном листе. Если ячейки, по данным которых требуется построить диаграмму, не являются смежными (расположены вразброс), то следует выделить первую группу ячеек, содержащих необходимые данные. Затем, удерживая нажатой клавишу Ctrl, выделить все остальные ячейки, значения которых требуется показать на диаграмме. Несмежные ячейки должны образовывать прямоугольник. Диаграмма может быть внедрена в рабочий лист или помещена на отдельном листе.
2.3 Контрольные вопросы 2.3.1 Что называют основанием системы счисления? 2.3.2 Что называется кодировкой информации? Сколько байт занимает 1 символ в памяти компьютера? 2.3.3. По каким правилам формируется формула? 2.3.4 Что представляет собой ссылка на диапазон ячеек? В чем разница между абсолютной и относительной ссылками? 2.3.5 Что представляет собой функция? Назовите составляющие функции. Перечислите функции, использованные в расчетно-графической работе, и укажите их назначение. 2.3.6 Какие возможности предоставляет Пакет анализа? 2.3.7 Назовите особенности вложенных функций. Сколько допускается вложенностей? 2.3.8 Для чего служит условное форматирование? В чем его особенности? 2.3.9 Перечислите компоненты диаграммы. 2.3.10 Что представляют собой списки? Каким образом осуществляется в списках сортировка, отбор данных и их анализ? Задание на расчетно-графическую работу 3.1.1 Используя известные базовые алгоритмические структуры и методики перевода чисел из одной системы счисления в другую, составить программу для выполнения задания 2.1.1. При разработке программы следует учесть возможность многократного ввода исходных данных (перевода нескольких чисел за один сеанс работы программы). 3.1.2 Используя известные базовые алгоритмические структуры выполнить задание 2.1.3. Вывести на экран данные, иллюстрирующие изменение уровня в резервуаре, с соответствующими комментариями и рекомендациями. Создать исполняемый файл с расширением.exe. 3.1.3 Вычислить значения функции f(x) (таблица Г.1) в интервале изменения аргумента [a, b] с заданным шагом h и вывести их на экран. Над полученными результатами выполнить требуемые действия. При решении задачи использовать тот вид оператора цикла, который указан для выбранного варианта. 3.1.4 Используя известные базовые и дополнительные алгоритмические структуры, решить предложенную задачу: а) варианты 1 – 8. Известно, что плотность жидкости r обычно измеряют при температуре 293 К. Для определения плотности при других температурах используют зависимость r(Т). Используя данные таблицы Г.2, рассчитать значения плотности в указанном интервале изменения температур и вывести их на экран. Определить среднее значение плотности при указанных колебаниях температуры; б) варианты 9 – 17. Для определения коэффициента гидравлического сопротивления l используют зависимость l(Re). Используя данные таблицы Г.2, рассчитать значения гидравлического сопротивления в указанном интервале изменения числа Рейнольдса Re и вывести их на экран. Определить модуль разности гидравлических сопротивлений, полученных при минимальном и максимальном числах Re; в) варианты 18 – 25. Для определения давления в трубопроводе используется зависимость p(x). Используя данные таблицы Г.2, определить распределение давления в указанных сечениях трубопровода х и вывести их на экран. Определить сечение, в котором давление р принимает значение 0,75рн. Значения начального рн и конечного рк давлений даны в МПа. Рекомендации к выполнению задания. При разработке программы желательно использовать ввод и вывод данных с комментарием. 3.1.5 Составить программу для выполнения задания 2.1.7. Предусмотреть возможность форматного вывода результатов на экран, а также возможность выбора из основного меню программы одного из пунктов задания 2.1.7 (задача а, б или в). 3.1.6 Составить программу для выполнения задания 2.1.8. Предусмотреть возможность форматного вывода результатов на экран. 3.1.7 Даны векторы a и b (таблица Г.3). Найти длины этих векторов, их скалярное произведение, а также косинус угла между ними. Предусмотреть возможность ввода данных пользователем, а также получение инструкций (справки) по использованию формул для вычислений. 3.1.8 Для хранения сыпучих веществ применяется цилиндрический бункер с конической нижней частью, из которой выгружается содержимое бункера (рисунок 3.1).
Рисунок 3.1 – Бункер для хранения сыпучих веществ До тех пор, пока высота h засыпанного в конус вещества не превышает высоты конической части бункера hконуса, его объем вычисляется по формуле Язык программирования для выполнения расчетно-графической работы выбирается согласно рекомендациям преподавателя. Все задания выполняются на дискете и оформляются пояснительной запиской. Пояснительная записка должна содержать вариант задания, блок-схему, текст программы и полученные результаты. 3.2 Общие рекомендации к выполнению расчетно-графической работы 3.2.1 Базовые алгоритмические структуры К управляющим операторам для реализации базовых конструкций относятся: следование, ветвление, - цикл-пока; к дополнительным – выбор, цикл с заданным числом повторений, цикл-до. Любая из дополнительных конструкций легко реализуется через базовые. Перечисленные шесть конструкций были положены в основу структурного программирования - «программирования без goto». 3.2.2 Характерные приемы программирования На практике реализация всех характерных приемов программирования (таблица 3.1) сводится к следующему: - до открытия цикла задается начальное значение накапливаемого или предположительное значение искомого параметра; - внутри цикла выполняется непосредственно накапливание или поиск. Таблица 3.1 – Характерные приемы программирования
Примеры реализации алгоритмов и программы накапливания суммы, произведения, количества, а также поиска максимального и минимального значений приведены в [20]. 3.2.3 Создание исполняемого файла В зависимости от среды разработки исполняемый файл создается автоматически при выборе команды Build (Build all) меню Compile. Сохраняется файл на диске в указанном пользователем (или выбранном по умолчанию) месте. Если исполняемый файл на диске обнаружить не удается, то необходимо выполнить некоторые настройки среды разработки. Например, при работе в среде Turbo Pascal необходимо выполнить следующие действия: - в меню Options опция Linker в контейнере Link Buffer отметить Disk, тем самым, показывая, что исполняемый файл следует сохранить не в оперативной, а во внешней памяти; - в меню Options опция Directories в поле EXE & TPU directories указать место на диске, куда следует сохранить исполняемый файл; - в меню Options опция Environment - Preferences в контейнере Auto save проверить отмечена ли Environment, т.е. убедиться в том, что настройки среды будут автоматически сохранены при их изменении и будут загружаться при открытии приложения. - в меню Options сохранить выбранные настройки с помощью опции Save.
3.3 Контрольные вопросы 3.3.1 Что представляет собой линейная структура? 3.3.2 Что представляет собой разветвляющаяся структура? 3.3.3 Что представляет собой цикл? 3.3.4 Какие алгоритмические структуры относят к базовым? 3.3.5 Какие алгоритмические структуры относят к дополнительным? 3.3.6 Что представляют собой характерные приемы программирования? 3.3.7 Какие файлы называются исполняемыми? Как они создаются? 3.3.8 Как осуществляется форматный и бесформатный ввод-вывод? 3.3.9 Какие конструкции для реализации ветвления предусмотрены в языке программирования, выбранном для выполнения расчетно-графической работы? 3.3.10 Какие конструкции для реализации циклов предусмотрены в языке программирования, выбранном для выполнения расчетно-графической работы?
Задание на расчетно-графическую работу 4.1.1 Создать базу данных в среде MS Access для заданной предметной области (таблица Д.1). База данных должна содержать не менее 3 таблиц. На схеме данных отобразить межтабличные связи с указанием типа отношения. Рекомендации к выполнению задания. При подборе информации для базы данных следует воспользоваться ресурсами Internet. 4.1.2 Для ввода данных в таблицы с помощью Мастера разработать соответствующие простые формы и внести не менее 20 записей в каждую таблицу. 4.1.3 Используя различные критерии отбора, с помощью конструктора создать три простых, три параметрических и один итоговый запрос. При создании итогового запроса допускается использование Мастера запросов. 4.1.4 Разработать сложную форму, используя Мастер форм, а также сформированные таблицы и запросы. 4.1.5 Сформировать отчеты, используя Мастер отчетов для создания и конструктор для редактирования, на базе разработанных запросов, включая итоговый отчет. 4.1.6 Разработать главную кнопочную форму и установить параметры загрузки базы данных.
4.2 Общие рекомендации к выполнению расчетно-графической работы 4.2.1 Создание таблиц Таблицы являются основными объектами реляционной базы данных. Ее структуру образуют поля (столбцы) и записи (строки). Поля обладают определенными свойствами (имя и тип). Существуют следующие способы создания пустой таблицы для последующего ее заполнения собственными данными: а) с помощью Мастера таблиц – поля для новой таблицы выбираются из различных образцов таблиц, имеющихся в Access; б) в режиме Конструктора – вручную в специальный бланк добавляются поля, настраивается их отображение, задается обработка данных, устанавливается первичный ключ; в) ввод данных непосредственно в пустую таблицу – при сохранении автоматически анализируются данные и каждому полю присваивается соответствующий тип. Также возможно создание таблиц на основе существующих данных следующими способами: а) с помощью импорта данных из другой базы данных MS Access или из файлов других программ; б) на основании данных из текущей таблицы при помощи запроса на создание таблицы. Запросы на создание таблиц можно использовать для архивирования старых записей, резервного копирования таблиц, выбора групп записей для экспорта в другую базу данных или для использования в качестве основы для отчетов, отражающих данные в определенный момент времени. Для создания таблицы одним из приведенных способов следует перейти в окно базы данных, выбрать в списке объектов Таблицы, способ создания и нажать на кнопку Создать. 4.2.2 Создание межтабличных связей После создания отдельных таблиц необходимо выбрать способ, которым MS Access будет вновь объединять сведения таблиц: следует определить связи между таблицами. Связь между таблицами устанавливает отношения между совпадающими значениями в ключевых полях, имеющими одинаковые имена в обеих таблицах. В большинстве случаев с ключевым полем одной таблицы, являющимся уникальным идентификатором каждой записи, связывается внешний ключ другой таблицы. Отображаются межтабличные связи на схеме данных. Отношение «один-ко-многим» является наиболее часто используемым типом связи между таблицами. В отношении «один-ко-многим» каждой записи в таблице A могут соответствовать несколько записей в таблице B, но запись в таблице B не может иметь более одной соответствующей ей записи в таблице A. Создается в том случае, когда только одно из полей является полем первичного ключа или уникального индекса. При отношении «многие-ко-многим» одной записи в таблице A могут соответствовать несколько записей в таблице B, а одной записи в таблице B несколько записей в т
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 423; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.21.176 (0.012 с.) |


 и объемную скорость потока V = v *S. Определить какого диаметра должна быть труба, чтобы скорость потока жидкости снизилась до 1,3 м/с при неизменной объемной скорости потока;
и объемную скорость потока V = v *S. Определить какого диаметра должна быть труба, чтобы скорость потока жидкости снизилась до 1,3 м/с при неизменной объемной скорости потока; где D - внутренний диаметр трубы, v - средняя скорость потока жидкости в трубе,
где D - внутренний диаметр трубы, v - средняя скорость потока жидкости в трубе,  - плотность жидкости,
- плотность жидкости,  - абсолютная вязкость жидкости. Если для потока жидкости в трубе величина числа Рейнольдса не превышает 2100, поток считается ламинарным. Если же его величина превышает 10000, поток считается турбулентным. Для значений, лежащих в диапазоне от 2100 до 10000, невозможно заранее определить тип потока. Найти число Рейнольдса и определить тип потока (ламинарный, турбулентный или неизвестный) для жидкостей, характеристики которых указаны в таблице Б.7.
- абсолютная вязкость жидкости. Если для потока жидкости в трубе величина числа Рейнольдса не превышает 2100, поток считается ламинарным. Если же его величина превышает 10000, поток считается турбулентным. Для значений, лежащих в диапазоне от 2100 до 10000, невозможно заранее определить тип потока. Найти число Рейнольдса и определить тип потока (ламинарный, турбулентный или неизвестный) для жидкостей, характеристики которых указаны в таблице Б.7.

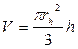 , где rh – радиус конической части бункера на высоте h,связанный с высотой h соотношением
, где rh – радиус конической части бункера на высоте h,связанный с высотой h соотношением  . Если высота хранящегося в бункере продукта h превышает высоту его конической части, то к объему конуса следует прибавить объем цилиндрической части бункера
. Если высота хранящегося в бункере продукта h превышает высоту его конической части, то к объему конуса следует прибавить объем цилиндрической части бункера 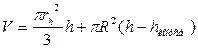 . Используя данные таблицы Г.4, вычислить объем бункера и значение угла j. Вывести на экран данные, иллюстрирующие зависимость объема засыпанного вещества от высоты h для набора значений в диапазоне от 0 до h (с шагом 0.25).
. Используя данные таблицы Г.4, вычислить объем бункера и значение угла j. Вывести на экран данные, иллюстрирующие зависимость объема засыпанного вещества от высоты h для набора значений в диапазоне от 0 до h (с шагом 0.25).


