
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операция соединения (основная).Содержание книги
Поиск на нашем сайте
Существует внутренняя операция соединения и внешняя, при этом внешняя делится на правую и левую. · Внутренняя а) естественное соединение – осуществляется по равенству значений в одноименных столбцах. Одноименные столбцы имеют одно и тоже имя и определены на одних и тех же доменах. Для соединения используются две таблицы, в результате получаем третью таблицу, кортежи которой получаются комбинацией тех кортежей из исходных таблиц, которые имеют одинаковые значения в одноименных столбцах. Операция соединения коммутативна относительно операндов, т.е. от перестановки мест результат не изменяется.
112 11a 112a 113 11b 112b 123 42c 113a 145 113b 421 421c операция соединения для таблиц с одинаковыми схемами равносильна операции пересечения:
11 11 11 12 42 42 Операция соединения для таблиц с разными схемами равносильна декартовому произведению:
11 cd 11cd 12 c1d 11c1d 14 12cd 42 12c1d 14cd 14c1d 42cd 42c1d
б) Тета-соединение ( Это соединение не обязательно по равенству, операция соединения происходит по любой операции сравнения( Тета-соединение осуществляется не обязательно по одноименным столбцам, а по разным тоже, но столбцы должны быть определены на одних и тех же доменах.
B=D a1c 1e a1c1e a12c 1e1 a1c1e1 a11c2 2e a2c2e a13c 2e1 a12c2e1 a11c21e a11c21e1
B>D a1c 1e a12c1e a12c 1e1 a12c1e1 a11c2 2e a13c1e1 a13c 2e1 a13c1e a13c2e a13c2e · Внешнее соединение. Рассмотрим на примере естественного соединения. тогда внешнее соединение выполняется по тем же правилам, что и естественное, но в ответ выписываются строки из левой таблицы, если соединение левое (из правой таблицы, если соединение правое). Пример:
left 1ac 1d 1acd 2a1c 2d 1acd1 1ac1 1d1 2a1cd 3ac 1ac1d 4a1c 1ac1d1 3ac null 4a1c null Свойства операции: 1. С помощью операции соединения можно выполнить операцию селекции, при этом операция селекции равносильна квантору существования. Если дано r (R) и необходимо выполнить операцию селекции
2. Операция соединения коммутативна. 3. Операция соединения ассоциативна: 4. Операция соединения дистрибутивна относительно операций пересечения, объединения и разности.
5. свойство идемпотентности: q 6. свойство полусоединения: Разложение без потерь. Теорема. Примеры Реляционная алгебра. Реляционная алгебра представляет собой основу доступа к реляционным данным. Основная цель алгебры – обеспечить запись выражений. Реляционная алгебра, определенная Коддом состоит из 8 операторов, составляющих 2 группы:
В основе реляционной модели лежит понятие «отношение». Отношение представляет собой подмножество декартова произведения доменов. Доменом называется некоторое множество допустимых значений, которое может принимать некоторый атрибут объекта. Декартовым произведением доменов D1, D2,...Dn называется
множество всех кортежей состоящих из k элементов - по одному из каждого домена. Таким образом декартово произведение позволяет получить все возможные комбинации из элементов доменов. Математически отношение записывается как
Кортежем называется элемент отношения. Математическое отношение используется двояко: 3. Для представления набора объектов (набор объектов - это множество подобных объектов). 4. Для предоставления связей между наборами объектов. Для представления набора объектов атрибуты соответствуют столбцами отношения. Множество допустимых значений атрибута соответствует соответствующему домену. Каждый кортеж отношения выполняет роль описания отдельного объекта из набора, при этом отношение выполняет роль описания всего набора объектов. Схемой отношения называют список имен атрибутов отношения. Если отношение R, а его схема имеет атрибуты A1,A2,...Ak, то схема отношения записывается как R(A1,A2,...Ak)
|
|||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 135; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.217.46 (0.009 с.) |

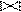 Обозначение: Join или.
Обозначение: Join или. 
 r(A,B,C) s(A,B,D) = q(A,B,C,D)
r(A,B,C) s(A,B,D) = q(A,B,C,D)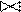 r(A,B) s(A,B) = q(A,B)
r(A,B) s(A,B) = q(A,B) r(A,B) s(C,D) = q(A,B,C,D)
r(A,B) s(C,D) = q(A,B,C,D) ).
). =(эквивалентное соединение),<>, <,>).
=(эквивалентное соединение),<>, <,>). r(A,B,C) s(D,E) = q (A,B,C,D,E)
r(A,B,C) s(D,E) = q (A,B,C,D,E)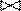 r(A,B,C) s(A,D) = q(A,B,C,D)
r(A,B,C) s(A,D) = q(A,B,C,D) , то ее можно выполнить с помощью операции соединения
, то ее можно выполнить с помощью операции соединения  .
.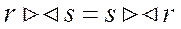
 =
= 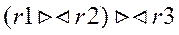
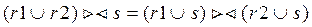

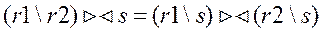
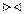 q=q; q
q=q; q 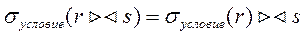 .
. где D1 = {d1.1,d1.2,...d1.k} и т.д.
где D1 = {d1.1,d1.2,...d1.k} и т.д.



