
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ряд послідовних фіксованих платежів, здійснюваних через рівні проміжки часу, називають фінансовою рентою або ануїтетом.Содержание книги
Поиск на нашем сайте Узагальнюючими показниками ануїтету є його майбутня і теперішня вартість. Майбутня вартість ануїтету – це сума всіх членів потоку платежів з нарахованими на них процентами на кінець періоду, тобто на дату останньої виплати. Вона показує, яку величину представлятиме капітал, що складається через рівні проміжки часу впродовж всього терміну ануїтету разом з нарахованими процентами. Коли платежі здійснюються щороку впродовж n років при процентній ставці i, майбутнє значення вартості ануїтету дорівнює:
де F – майбутня вартість ануїтету; A 1, A 2, …, A n – суми, що сплачуються в кінці кожного періоду в ануїтет; i – процентна ставка; n – кількість років. Якщо платежі в кожен період дорівнюють
Перемножуючи обидві сторони рівняння (1.18) на
Величина Формула (1.19) – це формула майбутньої вартості звичайного ануїтету, бо всі платежі (надходження) грошових коштів відбуваються в кінці періодів. Коли платежі відбуваються на початку кожного періоду, то в цьому разі ми маємо справу з авансовим ануїтетом. Його майбутня вартість визначається за формулою:
У цілому ряді практичних задач використовується значення не процентного фактора майбутньої вартості ануїтету, а його зворотна величина, яку називають процентним фактором фонду відшкодування. Припустимо, що величина F – це майбутня вартість боргових зобов’язань, і для її погашення необхідно створити фонд відшкодування. Для його створення потрібно в кінці кожного періоду вносити певну суму коштів, рівну величині A. Таким чином, величина щорічного внеску до фонду відшкодування дорівнюватиме:
(5) Під час використання процедур дисконтування грошових потоків при оцінці міжнародних інвестицій необхідно знати теперішню (інші назви – сучасну, приведену, поточну) вартість грошової суми, що може бути отримана в майбутньому. Якщо взяти формулу визначення майбутньої вартості грошей (1.7), то з неї можливо отримати вираз для розрахунку теперішньої вартості грошей:
Приймемо для зручності, що
В багатьох задачах, що постають на практиці, грошові кошти повинні надходити або вкладатися в кінці кожного року за певний проміжок часу. Теперішня вартість ряду платежів (або надходжень) є сумою щорічних окремих платежів (надходжень). Дана сума виражається такою формулою:
де PVA – теперішня вартість грошей, що повинна бути отримана. Якщо припустимо, що
Здійснивши відповідні математичні перетворення, отримаємо формулу (1.25):
Вираз Але
Звідси виводяться дві важливі формули взаємозв’язку процентних факторів теперішньої і майбутньої вартості ануїтетів:
Теперішня вартість авансового ануїтету визначається як:
Перпетуїтет – це ануїтет або серія періодичних платежів, що тривають нескінченно. Якщо n прагне до нескінченності, то з рівняння (1.24) отримаємо, що границя PVA дорівнює
де PV – теперішня вартість перпетуїтету; P – річний платіж; i – процентна ставка. Перелік питань для самоконтролю знань 1. Поясніть, на чому ґрунтується концепція вартості грошей у часі. 2. Обґрунтуйте, яким чином процентна ставка пов’язана з розумінням і визначенням майбутньої і теперішньої вартості грошей. 3. Покажіть, чим різняться і що спільного мають розрахунки, пов’язані з нарахуванням простих і складних процентів. 4. Доведіть, яким чином змінюються множники нарощування простих і складних процентів за умови їх нарахування декілька разів на рік (щопівріччя, щокварталу, щомісяця). 5. Аргументовано поясніть, чим відрізняються „німецька”, „французька” і „англійська” практика розрахунку процентних платежів. 6. Припустимо, проста і складна процентні ставки є рівними ( 7. Покажіть, яким чином можливо визначити час, необхідний для збільшення первісної суми коштів в N разів за простими і складними процентами. 8. Аргументовано поясніть, у чому полягають особливості майбутньої та теперішньої вартості ануїтету. 9. Покажіть, чим відрізняється авансовий ануїтет від звичайного. 10. Зазначте, який економічний зміст має та на чому ґрунтується визначення щорічного внеску до фонду відшкодування. 11. Поясніть, що являє собою сила зростання. 12. З’ясуйте, у чому полягає економічний зміст перпетуїтету та яким чином розраховується його теперішня вартість.
|
||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 483; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

 (1.17)
(1.17) то рівняння (1.17) може бути переписано таким чином:
то рівняння (1.17) може бути переписано таким чином: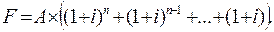 (1.18)
(1.18) й віднімаючи з нього рівняння (1.17), отримаємо:
й віднімаючи з нього рівняння (1.17), отримаємо: (1.19)
(1.19) називається процентним фактором майбутньої вартості ануїтету, що може бути визначений шляхом прямого обчислення на комп’ютері, або його значення може бути знайдене зі спеціальних таблиць. Позначимо його як PFFVAn,i.
називається процентним фактором майбутньої вартості ануїтету, що може бути визначений шляхом прямого обчислення на комп’ютері, або його значення може бути знайдене зі спеціальних таблиць. Позначимо його як PFFVAn,i.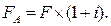 (1.20)
(1.20) (1.21)
(1.21) (1.22)
(1.22) Тоді PV – це теперішня вартість суми Sn, яку можна отримати, якщо б сума PV була вкладена на n років за складною процентною ставкою i:
Тоді PV – це теперішня вартість суми Sn, яку можна отримати, якщо б сума PV була вкладена на n років за складною процентною ставкою i: (1.23)
(1.23) – процентний фактор теперішньої вартості грошей, що показує, скільки потрібно зараз вкласти коштів за складною процентною ставкою i, щоб через n років отримати 1 грошову одиницю.
– процентний фактор теперішньої вартості грошей, що показує, скільки потрібно зараз вкласти коштів за складною процентною ставкою i, щоб через n років отримати 1 грошову одиницю. (1.24)
(1.24) то сума PVA є не чим іншим, як добутком величини S на суму n членів геометричної прогресії зі знаменником і першим членом
то сума PVA є не чим іншим, як добутком величини S на суму n членів геометричної прогресії зі знаменником і першим членом  і n -имчленом
і n -имчленом 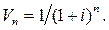 Тоді PVA дорівнює:
Тоді PVA дорівнює:
 (1.25)
(1.25) називається процентним фактором теперішньої вартості ануїтету. Позначимо його як PFPVAn,i.
називається процентним фактором теперішньої вартості ануїтету. Позначимо його як PFPVAn,i.
 (1.26)
(1.26) (1.27)
(1.27) (1.28)
(1.28)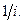 Тоді:
Тоді: (1.29)
(1.29) ). Доведіть, що при
). Доведіть, що при  нарощена сума, що обчислена за простими процентами, буде більшою від нарощеної суми, обчисленої за складними процентами, а при
нарощена сума, що обчислена за простими процентами, буде більшою від нарощеної суми, обчисленої за складними процентами, а при  – навпаки.
– навпаки.


