Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приклад рiшення завдання контрольної роботиСодержание книги
Поиск на нашем сайте
Контрольна робота для студентів заочної форми навчання передбачає рішення шести завдань, варіанти яких наведені у розділах даного посібника: 1) завдання 1.5.1 – стор.15, 2) завдання 2.4.3 – стор.26, 3) завдання 2.4.2 – стор.25, 4) завдання 4.4.3 – стор.49, 5) завдання 5.5.3 – стор.61, 6) завдання 6.5 – стор.82.
1.Перевести числа K,L,M з однієї системи числення до іншої:
K (dec) =... (bin) =... (hex), L (hex) =... (bin) =... (dec), M (bin) =... (hex) =... (dec).
Рiшення завдання 1.
Переведемо у двiйкову форму цiлу частину числа К дiленням його на 2: 2987 ¦ 1 2987 (dec) = 1011 1010 1011 (bin) 1493 ¦ 1 746 ¦ 0 373 ¦ 1 186 ¦ 0 93 ¦ 1 46 ¦ 0 23 ¦ 1 11 ¦ 1 5 ¦ 1 2 ¦ 0 Переведемо у двiйкову форму дробову частину числа К множенням його на 2:
0,46 0,46 (dec) = 0,0111 0101 (bin) 0,92 1,84 1,68 1,36 0,72 1,44 0,88 1,76
Таким чином:
K = 2987,46 (dec) = 1011 1010 1011,0111 0101(bin)
Пiсля замiни двiйкових тетрад шiстнадцятковими цифрами остаточно одержимо:
K= 2987,46 (dec) = 1011 1010 1011,0111 0101 (bin) = BAB,75(hex).
В числi L замiнимо шiстнадцятковi цифри двiйковими тетрадами:
L = 65B,3 (hex) = 0110 0101 1011,0011 (bin).
Згiдно iз правилом Горнера запишемо:
110 0101 1011,0011 (bin) = =1024 + 512 + 64 + 16 + 8 + 2 + 1 + 0,125 + 0,0625=1627,1875 (dec)
Таким чином:
L = 65B,3 (hex) = 0110 0101 1011,0011 (bin) = 1627,1875 (dec).
Пiсля замiни в числi М двiйкових тетрад шiстнадцятковими цифрами одержимо: М = 0010 1110 0010,0110 (bin) = 2E2,6 (hex).
Згiдно iз правилом Горнера запишемо:
10 1110 0010,0110 (bin) = = 512 + 128 + 64 + 32 + 2 + 0,25 + 0,125 = 738,375 (dec).
Таким чином:
М = 0010 1110 0010,0110 (bin) = 2E2,6 (hex) = 738,375 (dec).
Виконаємо в двійкових кодах додавання K+L:
+1011 1010 1011, 0111 0101 К 0110 0101 1011, 0011 L 10010 0000 0110, 1010 0101 K+L
K+M:
+1011 1010 1011, 0111 0101 К 0010 1110 0010, 0110 M 1110 1000 1101, 1101 0101 K+M
M+L:
+0010 1110 0010, 0110 M 0110 0101 1011, 0011 L 1001 0011 1101, 1001 M+L
2.Виконати логiчнi функцiї I,ЧИ,I-HE,ЧИ-HE, ВИНЯТКОВЕ ЧИ для змiнних
X = 7С4А (hex), Y = 3Е19 (hex).
Рiшення завдання 2.
Представимо змiннi Х та Y в двiйковiй формi X (bin) = 0111 1100 0100 1010 Y (bin) = 0011 1110 0001 1001
Для знаходження результату логiчноi функцii I знаходимо в змiнних X та Y пару одиниць, пiд ними запишемо одиницi, пiд iншими парами запишемо нулi:
X (bin) = 0111 1100 0100 1010 Y (bin) = 0011 1110 0001 1001 X Ù Y = 0011 1100 0000 1000 = 3C08 (hex).
Проiнвертувавши результат, одержимо логiчну функцiю I-НЕ: _____ X Ù Y = 1100 0011 1111 0111 = С3А7 (hex). Для знаходження результату логiчноi функцii ЧИ знаходимо в змiнних X та Y пару нулiв, пiд ними запишемо нулi, пiд iншими парами запишемо одиницi:
X (bin) = 0111 1100 0100 1010 Y (bin) = 0011 1110 0001 1001 X ÚY = 0111 1110 0101 1011 = 7E5B (hex).
Проiнвертувавши результат, одержимо логiчну функцiю ЧИ-НЕ: ____ X Ú Y = 1000 0001 1010 0100 = 81А4 (hex).
Для знаходження результату логiчноi функцii ВИНЯТКОВЕ ЧИ знаходимо в змiнних X та Y однакову пару нулiв або одиниць, пiд ними запишемо нулi, пiд неоднаковими парами запишемо одиницi:
X (bin) = 0111 1100 0100 1010 Y (bin) = 0011 1110 0001 1001 X Y = 0100 0010 0101 0011 = 4253 (hex).
3.Скласти та мiнiмiзувати логiчне рiвняння в ДДНФ для таблицi iстинностi (A,B,C,D - входи, Y - вихiд):
Рiшення завдання 3
Видiлимо рядки iз одиничними значеннями вихiдного сигналу Y (рядки 4,5,8,9,11,12,14,15), складемо рiвняння iз восьми добуткiв AÙBÙCÙD та поставимо знаки iнверсii над змiнними A,B,C,D, якi у видiлених рядках мають нульовi значення:
─ ─ ─ ─ ─ ─ ─ ─ ─ ─ ─ Y = AÙBÙCÙDÚAÙBÙCÙDÚAÙBÙCÙDÚAÙBÙCÙDÚAÙBÙCÙDÚ 1 2 3 4 5 ─ ─ ─ ÚAÙBÙCÙDÚAÙBÙCÙDÚAÙBÙCÙD; 6 7 8
Використаємо закон склеювання попарно для доданкiв 1-3, 4-5, якi вiдрiзняються один вiд одного тiльки однiєю змiнною, яка виключається: ─ ─ ─ ─ ─ ─ ─ ─ Y = AÙCÙDÚAÙBÙCÙDÚAÙBÙDÚAÙBÙCÙDÚAÙBÙCÙDÚ 1-3 2 4-5 6 7 ─ ÚAÙBÙCÙD;
Для доданкiв 1-3 та 6 використаємо послiдовно закон дистрибутивностi та наслiдок: ─ ─ ─ ─ ─ ─ ─ ─ ─ Y=CÙDÙ(AÚAÙB)ÙAÙBÙCÙDÚAÙBÙDÚAÙBÙCÙDÚAÙBÙCÙD= 1-3-6 2 4-5 7 8 ─ ─ ─ ─ ─ ─ ─ ─ = CÙDÙ(AÚB)ÙAÙBÙCÙDÚAÙBÙDÚAÙBÙCÙDÚAÙBÙCÙD. 1-3-6 2 4-5 7 8
4.Здiйснити аналiз логiчної схеми. Вихiдну логiчну функцiю пpедставити аналiтичним виpазом, який пеpевести до базису ЧИ-НЕ i синтезувати схему у цьому базисі.
┌───┐ ┌───┐ Х1────┤ & │ ┌───────┤ & │ Х2────┤ O ──┘ X6───┤ ├─── X3──┬─┤ │ ┌──┤ │ │ └───┘ │ └───┘ │ ┌───┐ └────────┐ └─┤ 1 │ ┌───┐ │ X4──┬─┤ ├───────┤ & │ │ │ └───┘ ┌──┤ O ────┘ │ ┌───┐ │ └───┘ └─┤ 1 │ │ X5────┤ O ────┘ └───┘
Рiшення завдання 4.
Позначимо сигнали на виходах елементiв схеми: ┌───┐ ┌───┐ Х1────┤ & │Y1┌───────┤ & │ Y Х2────┤ O ──┘ X6───┤ ├─── X3──┬─┤ │ ┌──┤ │ │ └───┘ │ └───┘ │ ┌───┐ └────────┐ └─┤ 1 │Y2 ┌───┐ │ X4──┬─┤ ├───────┤ & │Y4 │ │ └───┘ ┌──┤ O ────┘ │ ┌───┐ │ └───┘ └─┤ 1 │Y3 │ X5────┤ O ────┘ └───┘ та запишемо вiдповiднi рiвняння:
Y2 = X3ÚX4;
─────── ───── Y = Y1ÙX6ÙY4 = X1ÙX2ÙX3 Ù X6 Ù (X3ÚX4) Ù (X4ÚX5). 1 2 3 4 5
Перш за все, позбавимось логiчних функцiй I. Cкориставшись правилом де Моргана, перетворимо логiчнi функцiї I, позначенi цифрами 3,4,5 у логiчнi функцiї ЧИ:
1 2
Аналогiчним чином перетворимо функцiї, позначенi цифрами 1 та 2:
Визначимо, що у вищенаведеному виразi вiдсутнi будь-якi логiчнi функцii, крiм функцiй НЕ та ЧИ-НЕ. Проведемо синтез схеми згiдно останнього виразу.
┌─┐ ┌─┐ X1─│ O ──┐ X6─│ O ─┐ ┌───┐ └─┘ │ ┌───┐ └─┘ └─┤ 1 │ ┌─┐ └───┤ 1 │ ┌───────┤ │ Y Х2─│ O ──────┤ O ──┘ X5───┤ O ─── └─┘ ┌─┤ │ ┌──────┤ │ ┌─┐ │ └───┘ │ ┌──┤ │ X3─┬─┤ O ──┘ ┌───┐ │ │ └───┘ │ └─┘ ┌───┤ 1 │ │ │ └─────┘ ┌─┤ О ──┘ │ │ └───┘ │ X4─────────┴────────────┘
5. В додатковому кодi виконати аpифметичну опеpацiю додавання знакових двобайтових опеpандiв X та Y, пpедставлених в пpямому кодi. Результат пеpевести в пpямий код. Визначити наявнiсть або вiдсутнiсть пеpеповнення.
Рiшення завдання 5
1. Представимо змiннi Х та У в двiйковiй формi у прямих кодах:
1) Х = 0.011 0101 1011 1100 - число додатнє, У = 1.001 1110 0101 0010 - число вiд'ємне.
2) Х = 1.011 0100 0101 0110 - число вiд'ємне, У = 1.010 0111 1000 1001 - число вiд'ємне.
3) Х = 1.011 0010 - число вiд'ємне, У = 1.011 0110 1010 0011 - число вiд'ємне.
4) Х = 0.100 0011 - число додатнє, У = 1.100 1111 0100 0111 - число вiд'ємне. 2. Представимо змiннi Х та У у додаткових кодах, для чого проiнвертуємо цифрову частину вiд'ємних чисел і додамо одиницю:
1) Х = 0.011 0101 1011 1100 - число додатнє, У = 1.110 0001 1010 1110 - число вiд'ємне.
2) Х = 1.100 1011 1010 1010 - число вiд'ємне, У = 1.101 1000 0111 0111 - число вiд'ємне.
3) Х = 1.100 1110 - число вiд'ємне, У = 1.100 1001 0101 1101 - число вiд'ємне.
4) Х = 0.100 0011 - число додатнє, У = 1.011 0000 1011 1001 - число вiд'ємне.
3. Виконаємо додавання в перших двох задачах, де не потрiбно змiнювати розрядностi змiнних:
1) 0.011 0101 1011 1100 1.110 0001 1010 1110 10.001 0111 0110 1010 └┘┘ 1 1 - бiти однаковi, переповнення немає, результат в прямому кодi:
Х + У = 0.001 0111 0110 1010 bin = 176А hex,
2) 1.100 1011 1010 1010 1.101 1000 0111 0111 11.010 0100 0010 0001 └┘┘ 1 1 - бiти однаковi, переповнення немає, результат в прямому кодi:
Х + У = 0.101 1011 1101 1111 bin = 5ВDF hex.
Для другої та третьої задач перед додаванням попередньо розширимо знак змiнних Х:
3) 1.111 1111 1100 1110 1.100 1001 0101 1101 11.100 1001 0010 1011 └┘┘ 1 1 - бiти однаковi, переповнення немає, результат в прямому кодi:
Х + У = 0.011 0110 1101 0101 bin = 36d5 hex.
4) 0.000 0000 0100 0011 1.011 0000 1011 1001 1.011 0000 1111 1100 └┘┘ 0 0 - бiти однаковi, переповнення немає, результат в прямому кодi:
Х + У = 0.100 1111 0000 0100 bin = 4F04 hex.
6. Потактно виконати множення беззнакових змiнних Х та У. Використати алгоритм множення фiксуванням множника Х, зсувом суми часткових добутків у вiдповiдностi iз аналiзом змiнноi У старшими бітами вперед. Шiстнадцятковi значення змiнних: X = СD42, У = 83A.
Рiшення завдання 6
Визначимо, що добуток 16-розрядноi змiнноi Х на 12-розрядну змiнну У матиме 28 розрядiв. Збiльшимо розряднiсть змiнноi Х до 28 нульовими бiтами i запишемо змiннi Х та У у двiйковiй формi: Х = 0000 0000 0000 1100 1101 0100 0010 У = 1000 0011 1010
Такт 1: 0000 0000 0000 1100 1101 0100 0010 - змiнна Х 0000 0000 0000 0000 0000 0000 0000 - початкова сума частко- вих добуткiв (CЧД0) 0000 0000 0000 1100 1101 0100 0010 - СЧД пiсля першого так- ту (СЧД1)
В тактах 2...6 додавання не вiдбуватиметься, тому, що вiдповiднi бiти змiнноi У дорiвнюють нулю.
Такт 7: 0000 0000 0000 1100 1101 0100 0010 - змiнна Х 0000 0011 0011 0101 0000 1000 0000 - СЧД1,зсунута влiво на 6 розрядiв 0000 0011 0100 0001 1101 1100 0010 - СЧД7
такт 8: 0000 0000 0000 1100 1101 0100 0010 - змiнна Х 0000 0110 1000 0011 1011 1000 0100 - СЧД7 * 2 0000 0110 1001 0000 1000 1100 0110 - СЧД8
такт 9: 0000 0000 0000 1100 1101 0100 0010 - змiнна Х 0000 1101 0010 0001 0001 1000 1100 - СЧД8 * 2 0000 1101 0010 1101 1110 1100 1110 - СЧД9
В тактi 10 додавання не вiдбуватиметься.
Такт 11: 0000 0000 0000 1100 1101 0100 0010 - змiнна Х 0011 0100 1011 0111 1011 0011 1000 - СЧД9 * 4 0011 0100 1100 0100 1000 0111 1010 - СЧД11
В тактi 12 додавання не вiдбуватиметься, тобто сума часткових добуткiв 11-го такту є кiнцевою.
Таким чином, Х * У = 34С487A hex. Л І Т Е Р А Т У Р А
1. Блейксли Т.Р. Проектирование цифровых устройств с малыми и большими интегральными схемами. – К.:Вища шк.,1981. 2. Грицевский П.М., Мамченко А.Е., Степенский Б.М. Основы автоматики, импульсной и вычислительной техники. – М.: Сов. радио,1979. 3. Кирилличев А.М. Основы вычислительной техники. – М.: Недра, 1979. 4. Майоров С.А., Новиков Г.И. Структура электронных вычислительных машин. – Л.: Машиностроение,1979. 5. Нешумова К.А.Электронные вычислительные машины и системы. – М.: Высш.шк.,1989. 6. Потемкин И.С.Функциональные узлы цифровой автоматики. –М.: Энергоатом издат,1988. 7. Прикладная теория цифровых автоматов/К.Г.Самофалов и др. – К.: 1987. 8. Савельев А.Я.Пpикладная теоpия цифpовых автоматов. – М.: Высш.шк., 1987. 9. Сергеев Н.П.,Вашкевич Н.П.Основы вычислительной техники. – М.: Высш.шк.1988. 10. Скаржепа В.А., Луценко А.Н. Электроника и микросхемотехника. Ч.1. Электронные устройства информационной автоматики. – К.: Вища шк., 1989. 11. Стрыгин В.В., Щарев Л.С. Основы вычислительной техники и программирования. – М.: Высш.шк.,1983. 12. Фpидман А.,Менон П. Теоpия и пpоектиpовавние пеpеключательных схем. – М.: Миp, 1978. 13. Цифровая и вычислительная техника/Под ред. Э.В. Евреи-нова. – М.: Радио и связь, 1991. 14. Янсен Й.Курс цифровой электроники: В 4-х т.Т.1.Основы цифровой электроники на ИС. – М.: Мир, 1987.
Навчальне видання
Комп’ютерна схемотехніка
Навчально-методичний посібник
Сергій Михайлович Іщеряков
Комп’ютерний набір Інна Пилипенко Комп’ютерна верстка оригінал-макету Іванна Михайлів Дизайн обкладинки Ольга Лобач
Підписано до друку 1.03.2004 р. Формат 60х841/16. Папір офсетний. Гарнітура Times New Roman. Друк офсетний. Умовн.вид.арк. 6,00. Обл.- вид.арк. 2,83. Тираж 150 прим. Зам. 44-1.
Інститут менеджменту та економіки “Галицька Академія” 76006, м.Івано-Франківськ, вул.Вовчинецька, 227, ІМЕ тел. факс (03422) 6-55-88 Віддруковано на поліграфічній дільниці видавничого відділу “Полум`я” Інституту менеджменту та економіки “Галицька Академія” тел. видавництва (03422) 9-30-71
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 181; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.67.237 (0.009 с.) |

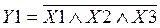 ;
; ;
;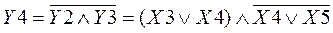 ;
;