
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Комплексне число як точка площини ⇐ ПредыдущаяСтр 3 из 3
У вибраній прямокутній системі координат число
Рис.1.1. Очевидно, що дійсні числа зображуються точками на осі Приклади. Знайти множину к.ч., що задовольняють умову:
Розв’язання. 1) Нехай Відповідь: множина чисел 2) Якщо
Відповідь: множина чисел Побудувати на площині ХОУ к.ч., записати їх дійсну та уявну частину. Обчислити модулі к.ч. 1. Відповіді. 1. 2. 3.
Коло, круг, кільце Нехай дано числа Рівнянню Очевидно, що нерівності Звернемо увагу на вироджені випадки кільця (1) (2) (3) (4) при
Рис. 1.2
Приклад. З’ясувати, чи належить точка Розв’язання. Порівняємо радіус
Відповідь: точка
Комплексне число як вектор
Кожному к.ч. Якщо вектор Нехай
Рис.1.3 Очевидно,
Множення і ділення к.ч.в геометричній формі розглядаються в §1.14.
Приклад. Доведемо нерівність Використовуємо простий факт: сума довжин довільних двох сторін трикутника більша довжини третьої сторони. З рис. 1.3 випливає, що Випадок чисел, розміщених на одній прямій пропонуємо розглянути самостійно. Приклад. Знайти суму і різницю Розв’язання.
Виконати самостійно В умовах попереднього прикладу знайти 2)
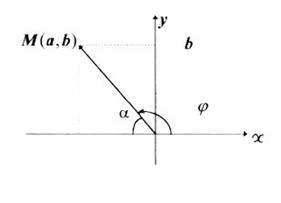
Кут нахилу вектора до осі
Розглянемо довільний ненульовий вектор
Рис. 1.4 Таким чином, кут нахилу задає напрямок вектора. З рис.1.4. випливає, що додатний j+ і від’ємний j- кути визначають один і той же напрямок. Очевидно також, якщо довільний кут j задає деякий напрямок, то такий же напрямок будуть задавати і кути Приклад. Легко перевірити, що кути 1350,4950,-2250,-9450 визначають один і той же напрямок (відносно осі
Аргумент комплексного числа Нехай вектор
Таким чином, аргумент к.ч. набуває нескінченну множину значень. Аргумент числа
Рис. 1.5 Найменше за абсолютною величиною значення Приклади. 1) Використовуючи рис. 1.6, легко переконатись, що
Рис. 1.6 2) Для довільного
Обчислення аргументу Спочатку відмітимо властивість: 1) Аргумент дійсного і чисто уявного числа: якщо
2) Аргумент будь-якого числа
Доведемо останню формулу у випадку, коли
Рис 1.7
Інші випадки розміщення числа Зауважимо, що вказаним способом для аргументу можна одержати формули, в яких використовуються арккотангенс, арккосинус чи арксинус. Якщо не вимагається високої точності, то аргумент к.ч. можна знаходити графічно. З цією метою слід побудувати к.ч. на міліметровому папері і виміряти відповідний кут за допомогою транспортиру. Цей спосіб іноді використовують для грубої перевірки обчислень. Приклад 1. Покажемо, як обчислюють аргументи чисел
Приклад 2. Достатньо встановити знаки дійсної і уявної частин к.ч., щоб перевірити рівності:
Tpигонометрична форма к.ч.
Нехай відомі модуль У випадку розміщення осей
Остання форма запису комплексного числа називається тригонометричною. Як бачимо, щоб знайти тригонометричну форму, досить обчислити модуль і аргумент к.ч. Приклади. Записати в тригонометричній формі слідуючі числа: 1) Розв’язання 1) Відповідь: 2) Відповідь: 3) Відповідь: Розглянемо алгоритм переходу від алгебраїчної до тригонометричної форми к.ч. Нехай дано к.ч. 1. Побудувати на площині ХОУ к.ч.
2. Знаходимо модуль к.ч.
На прикладі маємо:
3. За допомогою таблиць або мікрокалькулятора знаходимо
На прикладі: 4. За формулою (1.1) § 1.14 знаходимо
5. Підставимо знайдені
Для
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 201; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.119.251 (0.054 с.) |
 зображається точкою
зображається точкою  (рис.1.1). Навпаки, якщо задана точка
(рис.1.1). Навпаки, якщо задана точка 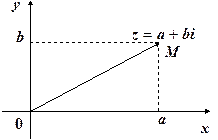
 , а чисто уявні - на осі
, а чисто уявні - на осі  ; з цієї причини
; з цієї причини  називають комплексною площиною, а к.ч. - точками цієї площини.
називають комплексною площиною, а к.ч. - точками цієї площини. ;
; .
. . Умову перепишемо в рівносильній формі:
. Умову перепишемо в рівносильній формі: 
 пряма
пряма 

 , отже,
, отже, 
 - півплощина, що розміщена нижче прямої
- півплощина, що розміщена нижче прямої  .
. . 2.
. 2.  . 3.
. 3. 







 .
.
 задовольняють всі числа (і тільки вони), що розміщені на колі радіуса
задовольняють всі числа (і тільки вони), що розміщені на колі радіуса  з центром у точці
з центром у точці  . Дійсно, якщо
. Дійсно, якщо 
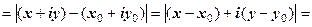
 .
. і
і  задають відповідно круг і кільце. На рис. 1.2 зображено кільце
задають відповідно круг і кільце. На рис. 1.2 зображено кільце  з центром у точці
з центром у точці  .
. – круг з виключеним центром
– круг з виключеним центром 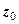 ;
; – зовнішність круга
– зовнішність круга  – круг з границею;
– круг з границею; – вся площина з виключеною точкою
– вся площина з виключеною точкою  маємо пусту множину.
маємо пусту множину.
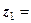 p до круга
p до круга  .
. з відстанню
з відстанню  від центра круга
від центра круга 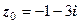 до точки
до точки  .
. , і навпаки, кожному радіусу-вектору
, і навпаки, кожному радіусу-вектору 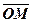 або довільним направленим відрізком, який при паралельному переносі збігається з
або довільним направленим відрізком, який при паралельному переносі збігається з  зображає к.ч.
зображає к.ч. 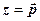 .
. Розглянемо паралелограм
Розглянемо паралелограм  , див. рис.1.3.
, див. рис.1.3.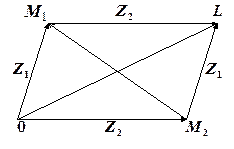

 , тобто сума і різниця к.ч. відповідають сумі і різниці векторів. Таким чином, додавання і віднімання набуває простого геометричного змісту.
, тобто сума і різниця к.ч. відповідають сумі і різниці векторів. Таким чином, додавання і віднімання набуває простого геометричного змісту. , яка є узагальненням нерівності абсолютних величин дійсних чисел.
, яка є узагальненням нерівності абсолютних величин дійсних чисел. , тобто
, тобто  .
. і
і  , де
, де  ,
,  . Переконатися за допомогою геометричної побудови, що ці вектори можна додавати і віднімати за правилом паралелограма.
. Переконатися за допомогою геометричної побудови, що ці вектори можна додавати і віднімати за правилом паралелограма.
 .
. ,
,  ;
; ,
,  .
. до суміщення її з напрямком вектора
до суміщення її з напрямком вектора  , якщо обертання здійснюється проти годинкової стрілки, і j
, якщо обертання здійснюється проти годинкової стрілки, і j  при обертанні за годинковою стрілкою; якщо напрямок
при обертанні за годинковою стрілкою; якщо напрямок  .
.
 , де
, де 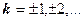 . Отже, за кут нахилу вектора
. Отже, за кут нахилу вектора  ціле число.
ціле число. називається будь-яке із значень кута нахилу вектора
називається будь-яке із значень кута нахилу вектора  , де
, де  .
. не визначається.
не визначається.
 (тобто значення з інтервалу
(тобто значення з інтервалу  ) називається головним значенням аргументу к.ч. і позначається
) називається головним значенням аргументу к.ч. і позначається  , тому
, тому  ,
, 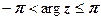 .
.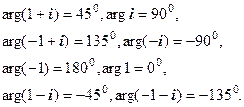

 . Пропонуємо довести цю тотожність самостійно.
. Пропонуємо довести цю тотожність самостійно.
 , то
, то 
 можна знаходити за формулою:
можна знаходити за формулою: (1.1)
(1.1) зображується точкою
зображується точкою  в другій чверті (рис.1.7). З
в другій чверті (рис.1.7). З 
 . Оскільки
. Оскільки  , то
, то 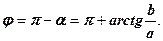
 за допомогою формул цього пункту.
за допомогою формул цього пункту. , (застосована формула (1.1),
, (застосована формула (1.1), 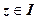 чверті);
чверті); , (формула (1.1),
, (формула (1.1),  чверті);
чверті); , (формула (1.1),
, (формула (1.1),  чверті);
чверті);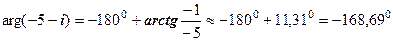 , (формула (1.1),
, (формула (1.1),  чверті);
чверті); ,
, .
.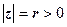 і аргумент
і аргумент  к.ч.
к.ч.  - полярні координати точки
- полярні координати точки  . Додамо ці рівності, помноживши другу на
. Додамо ці рівності, помноживши другу на  :
:
 2)
2)  3)
3) 
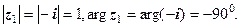


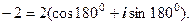

 .
. . Для переходу до тригонометричної форми необхідно:
. Для переходу до тригонометричної форми необхідно: і встановити, до якої чверті належить
і встановити, до якої чверті належить 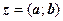 . На даному прикладі:
. На даному прикладі: 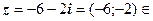 ІІІ четв. Див. рис.
ІІІ четв. Див. рис.
 (1)
(1)
 , ураховуючи при цьому властивість
, ураховуючи при цьому властивість .
. .
. . Для даного прикладу:
. Для даного прикладу:  ІІІ чверті. Маємо:
ІІІ чверті. Маємо:
 і
і  (2)
(2) маємо:
маємо:



