
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Квадратні рівняння з від’ємними дискримінантами
Відомо, що корені квадратного рівняння
знаходяться за формулами
де вираз При D >0 корені квадратного рівняння дійсні і різні; при D =0 корені дійсні і рівні; при D <0 говорять. що дійсні корені не існують, а існують, так звані, комплексні корені. Приклад. Знайти корені квадратного рівняння
За формулами (2) маємо:
Серед дійсних чисел вираз Символ
його називають уявною одиницею. Тепер корені рівняння
Перевірка. Для
Аналогічно робиться перевірка для Отже, для квадратного рівняння
Приклади для самостійного розв’язання Розв’язати квадратні рівняння: 1. 3. 5. 7. 9. Відповіді. 1.
Алгебраїчна форма к.ч. В алгебраїчній формі к.ч.мають вигляд Два к.ч. називаються рівними, якщо відповідно рівні їх дійсні та уявні частини. Основні операції над к.ч. в алгебраїчній формі введені в §§4.4,4.5,4.6. Надалі домовимось вирази Нехай дано число Приклад. Розв’язати рівняння Розв¢язання. З рівності к.ч. випливає:
Спряжені к.ч.
Числа Очевидно, якщо Приклади. 1) Якщо 2) Безпосередньо перевіряється тотожність
Модуль к.ч.
Модулем числа Модуль дійсного числа дорівнює його абсолютній величині. Справді, якщо Приклади. 1) 2) 3) 4) Показати, що модулі спряжених чисел рівні. Розв¢язання. Досить обчислити модулі спряжених чисел
Додавання і віднімання к.ч.
Приклади 1. 2. Обчислити самостійно 1. 3. 5. 7. 9. Відповіді. 1. 8.
Множення к.ч.
Множення к.ч. виконуємо згідно правила (вважаючи, що
Приклади.
Правильна тотожність
Спростити самостійно 1. 3. 5. 7. Відповіді. 1. 6.
Ділення к.ч.
Ділення к.ч. виконується згідно правила (при умові
Приклади. 1)
2) 3) Розв’язати рівняння Розв’язання. Перевірка:
Спростити самостійно вирази 1. Відповіді. 1.
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 77; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.154.103 (0.028 с.) |
 (1)
(1) (2)
(2) називають дискримінантом.
називають дискримінантом.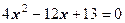 .
. .
.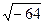 не має смислу, тобто
не має смислу, тобто  .
. прийнято позначати буквою і, тобто:
прийнято позначати буквою і, тобто: , а
, а 
 .
. маємо:
маємо:
 .
. .
. і
і 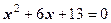 2.
2. 
 4.
4. 
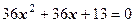 6.
6. 
 8.
8. 
 10.
10. 
 . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  . 5.
. 5. 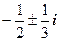 . 6.
. 6.  . 7.
. 7.  . 8.
. 8.  . 9.
. 9.  . 10.
. 10.  .
. , де
, де  дійсні числа; число
дійсні числа; число  називається дійсною, а
називається дійсною, а  – уявною частиною к.ч.; позначення:
– уявною частиною к.ч.; позначення:  ; символ
; символ 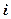 формально визначається рівністю
формально визначається рівністю 
 і т.п. вважати к.ч., записаними в алгебраїчній формі, отже,
і т.п. вважати к.ч., записаними в алгебраїчній формі, отже,  і т.п. набуватимуть тільки дійсних значеннь.
і т.п. набуватимуть тільки дійсних значеннь. , то
, то  дійсне число:
дійсне число: 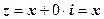 ; якщо
; якщо 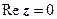 , то
, то  називається чисто уявним числом:
називається чисто уявним числом:  .
. ; де
; де  дійсні числа.
дійсні числа.
 . Розв’язуючи цю систему, одержимо
. Розв’язуючи цю систему, одержимо  .
. називаються спряженими. Таким чином, якщо
називаються спряженими. Таким чином, якщо  і
і  – спряжені числа, то
– спряжені числа, то  і
і  .
. дійсне число, то
дійсне число, то  ; якщо
; якщо  – чисто уявне число, то
– чисто уявне число, то  . Навпаки, якщо
. Навпаки, якщо 
 , то
, то  .
.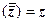 .
. називається невід’ємне число
називається невід’ємне число  .
. , то
, то  .
. .
.
 .
.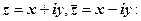



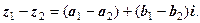
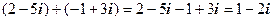 .
. .
. 2.
2. 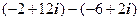
 4.
4. 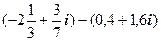
 6.
6. 
 8.
8. 
 10.
10. 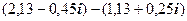
 . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  . 5.
. 5.  . 6.
. 6.  . 7.
. 7. 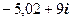 .
. . 9.
. 9.  . 10.
. 10.  .
.


 .
.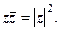

 2.
2. 
 4.
4. 
 6.
6. 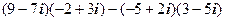

 . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  . 5.
. 5.  .
. . 7.
. 7.  .
.  ):
):





 Відповідь:
Відповідь: 
 2.
2.  3.
3.  .
. . 3.
. 3.  .
.


