Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистичні методи дослідження якості і надійностіСодержание книги
Поиск на нашем сайте
Виробів електронної техніки Мета роботи: провести кількісну оцінку результатів відбраковуючих випробувань
Теоретичні відомості Для оволодіння теорією і практикою вивчення надійності напівпровідникових виробів електронної техніки необхідно навчитися оперувати з|із| випадковими величинами, тобтовеличинами, які, в результаті|унаслідок,внаслідок| експерименту|досліду| можуть приймати те або інше значення, причому наперед|заздалегідь| невідомо, яке саме. Наприклад, випадковими величинами будуть: час|справленої| роботи виробу від початку експлуатації до його відмови або число відмов від загального|спільного| числа виробів, поставлених на випробування. Нехай|нехай| в результаті|унаслідок,внаслідок| експерименту|досліду| може з'явитися|появитися| або не з'явитися|появитися| деяка подія А. В цьому випадку замість події А можна розглядати|розглядувати| випадкову величину X, яка дорівнює 1, якщо подія А відбувається|походить|, і дорівнює 0, якщо подія А не відбувається|походить|. Випадкова величина X називається характеристикою випадкової величини події А. Експеримент|дослід| з|із| випадковими величинами може зводитися до схеми випадків або схеми рівноможливих результатів. Наприклад, для випадку випадання цифри при киданні монети ("решка") можна підрахувати|підсумувати|: випадок = 1 всього випадків 2. Випадок випадіння парного числа на кубику можна також підрахувати|підсумувати|: 3/6 = 1/2. У цих ситуаціях вірогідність|ймовірність| появи події може бути визначена наперед|заздалегідь| - до експерименту|досліду|. Таких випадків зустрічається мало. Переважна більшість завдань|задач| теорії надійності не можуть бути зведені до схеми випадків. В процесі випробувань якихось однотипних виробів з терміном служби вони можуть виходити з|із| ладу|строю,буд|. Час відмови для кожного виробу є величина випадкова і теоретично може приймати будь-які значення - від нуля до нескінченності. Будь-яке співвідношення, що встановлює зв'язок між можливими значеннями випадкових величин і їх вірогідністю|ймовірністю|, називається законом розподілу випадкової величини. Випадкові величини бувають дискретними (перервними) і безперервними. Наприклад, число відмов - дискретна величина. Час між відмовами - безперервна величина. Простим видом завдання|задавання| закону випадкової величини є|з'являється,являється| таблиця, наприклад, такого вигляду|виду|:
Закон розподілу, заданий у вигляді таблиці, одержав|отримав| назву ряду|лави,низки| розподілу. Найповніша характеристика випадкової величини задається її функцією розподілу, що вказує|вказує|, які значення і з|із| якою вірогідністю|ймовірністю| приймає задана величина. Проте|однак|, нерідко|незрідка| потрібні деякі більш загальні уявлення про випадкову величину. Для теорії надійності велике значення мають деякі постійні числа, що отримують|отримуються| за певними правилами з|із| функцій розподілу. Серед цих постійних, що служать для загальної|спільної| кількісної оцінки випадкових величин, для характеристики їх "в цілому|загалом|" особливе значення мають середнє значення (математичне очікування|чекання|), дисперсія, середньоквадратичне (стандартне) відхилення, мода і медіана. Нехай|нехай| випадкова величина х приймає значення, відповідно з|із| вірогідністю|ймовірністю| Математичним очікуванням|чеканням| випадкової величини (середнім її значенням) називається сума добутків|добутків| всіх можливих значень випадкової величини на їх вірогідності|ймовірності|:
Для безперервної випадкової величини середнє значення
Якщо випадкова величина х розподілена у відрізку ab, то
Загальні|спільні| властивості математичного очікування|чекання|: 1.Математичне очікування|чекання| постійної с дорівнює цій же постійній: М [с|із| ] = с. 2.Постійний множник виноситься за знак математичного 3.Математичне очікування|чекання| суми будь-яких випадкових величин 4.Математичне очікування|чекання| добутку|добутку| незалежних випадкових величин дорівнює добутку|добутку| їх математичних очікувань|чекань|: М [ху|] = М[х]· М[у]. Середнє значення не є|з'являється,являється| випадковою величиною. Воно надає числову характеристику розподілу вірогідності|ймовірності| випадкової величини. Для оцінки розкиду значень випадкової величини навколо|близько| її середнього значення використовується декілька числових характеристик, найважливішими з|із| яких є|з'являються,являються| дисперсія і середньоквадратичне (стандартне) відхилення. Під центрованою випадковою величиною, відповідній випадковій величині х, розуміють відхилення випадкової величини від її математичного очікування|чекання|: Дисперсією випадкової величини називається математичне очікування|чекання| квадрата відповідної центрованої величини: Нескладні перетворення алгебри і використання сформульованих вище властивостей математичного очікування|чекання| приводять|призводять,наводять| до рівняння Дисперсію можна розглядати|розглядувати| як міру розсіяння (розкиданості) значень випадкової величини від її середнього значення. Дисперсія має наступні|слідуючими| властивості: 1. Дисперсія постійної величини дорівнює нулю: D(c)= 0. 2. Дисперсія суми попарно незалежних випадкових величин дорівнює сумі дисперсій добутків:
Середньоквадратичне (стандартне) відхилення випадкової величини дорівнює позитивному значенню кореня квадратного з|із| математичного очікування|чекання| квадрата відхилення випадкової величини від її математичного очікування|чекання|:
Окрім|крім| математичного очікування|чекання| (середнього значення), положення|становище| випадкової величини на числовій осі визначається ще такими характеристиками розсіяння, як найменше (мінімальне) і найбільше (максимальне) значення, мода та медіана випадкової величини, квантилі. Модою (Мо|) випадкової величини називають її найбільше вірогідне значення. Модою безперервного розподілу, що має щільність F(x), називається абсциса х, при якій Р(х) досягає максимуму. Розподіл може бути одномодальним, двух-| і більш модальним і антимодальним. Мода випадкової величини може бути визначена з|із| рівняння Якщо екстремум функції F(x) існує, але|та| є|з'являється,являється| мінімумом, тобто Значення випадкової величини можуть бути впорядковані в наростаючій або зменшувальній послідовності. Значення випадкової величини, яке ділить впорядкований ряд|лаву,низку| на дві однакові частини, називається медіаною. Медіаною (Me) випадкової величини х називається таке її значення, для якого Різниця між максимальним і мінімальним значенням випадкової величини називається розмахом |уширшки| діапазону розсіяння: R = хмакс| - хмін|. Р-квантилем (хр|) називається значення випадкової величини, що задовольняє рівнянню Спеціальні квантилі: х 0,25 і х 0,75- квартілі|; х 0,50- медіана; х 0,10,х 0,20 ….,х0,90- децілі|; х 0,01,х 0,02…,х0,99 - процентілі.. Приклад. Проводилися дослідження впливу відбраковуючих| випробувань циклічної зміни температур і тривалої температурної дії на міцність клейового з'єднання|сполучення,сполуки| кристал - корпус функціонального елемента. Посадка кристалів площею|майданом| 1,2 мм2 в корпус типу 401.14-3 здійснювалася на клей ВК-32-200|. Одержані|отримані| дані представлені|уявлені| в таблиці 1 Таблиця 1 - Результати випробувань
Визначимо числові характеристики розподілу набутого значення руйнуючого зусилля зміщення|зсуву| кристалу. Одержані|отримані| дані представимо|уявимо| в табл. 2. Таблиця 2
Для практичного визначення медіанного і модального значень необхідно в табл. 1 значення розподілити у вигляді наростаючого ряду|лави,низки| (табл. 3). Таблиця 3
У розподіленому за збільшенням або зменшенням ряду|лаві,низці| значень при непарному числі виробів величина значення середнього в ряду|лаві,низці| і буде медіанним значенням. У разі|в разі| парного числа виробів медіанне значення дорівнює середньому значенню двох значень виробів у|в,біля| середині ряду|лави,низки|. Наприклад, для 20 виробів медіанним значенням буде середнє значення для значень 10-го і 11-го виробів. Стабільний технологічний процес виготовлення виробів електронної техніки характеризується межею розкиду параметрів, рівною ± Таблиця 4
Значення менше нуля не записується|занотовується|. За аналізом значень табл.2,3, 4, можна зробити наступні|слідуючі| висновки|виведення|: 1. Міцність клейового з'єднання|сполучення,сполуки| збільшується після|потім| дії відбраковуючих випробувань і термотренування при температурі+125°С, що видно|показно| зі збільшення мінімального, максимального і середнього значень по операціях. 2. Дія 100 термоциклів| декілька знижує міцність клейового з'єднання,|сполучення,сполуки| в порівнянні з попереднім станом, що видно|показно| по мінімальному та максимальному значеннях, хоча середнє значення залишається в тих же межах. 3.Розподіли значень руйнуючих зусиль зміщення|зсуву| по операціях I, II, III - одномодальні, по операції IV - двомодальне. 4.Розкид значень руйнуючого зусилля зміщення|зсуву| кристалів для Порядок виконання роботи 1. Результати випробувань занести до таблиці. 2. Для практичного визначення медіанного і модального значень необхідно значення розподілити у вигляді наростаючого ряду|лави,низки|. 3. Визначити числові характеристики розподілу набутого значення руйнуючого зусилля зміщення|зсуву| кристалу:
4. Визначити стабільність технологічного процесу за правилом «трьох сигм», або законом Гауса. 5. Зробити висновки за результатами проведених випробувань про можливість подальшого використання виробу електронної техніки.
Контрольні питання 1. Кількісні та якісні показники надійності. 2. Види випробувань на надійність. 3. Категорії випробувань. 4. Виробничий контроль та контроль готових виробів. 5. Визначення числових характеристик випадкових величин. Закон Гауса. Лабораторна робота №4
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 104; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.28.200 (0.011 с.) |


 .
.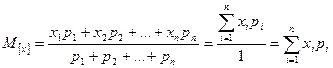

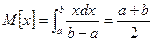 .
.

 .
.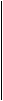



 Постійний множник виходить за знак дисперсії в квадраті:
Постійний множник виходить за знак дисперсії в квадраті: .
.
 за умови, що|при умові, що,при условии |
за умови, що|при умові, що,при условии |  , де
, де  - функція розподілу випадкової величини х.
- функція розподілу випадкової величини х. , такий розподіл називається антимодальним.
, такий розподіл називається антимодальним. або
або  .
. .
.

 , щодо|відносно| середнього значення. Тоді значення параметрів, що характеризують технологічний процес, запишемо в табл.4.
, щодо|відносно| середнього значення. Тоді значення параметрів, що характеризують технологічний процес, запишемо в табл.4.