В задаче ВПС требовалось оптимально выбрать пропускную способность каналов при заданной конфигурации потоков {  }. Здесь рассматривается обратная задача – задача распределения потоков(РП) при заданных пропускных способностях, а потоки надо определить так, чтобы минимизировать среднюю задержку. Ранее было отмечено, что допускающие альтернативу процедуры выбора маршрута, дающие более одного пути для трафика j-k оказываются хуже фиксированной процедуры выбора маршрута, в которой предполагается только один путь для этого трафика. Это замечание было основано на предположении, что пропускная способность может быть выбрана так, чтобы удовлетворить требованиям трафика. Здесь рассматривается ситуация, когда пропускные способности заданы, а потоки должны быть оптимально согласованы; поэтому, вероятно, может возникнуть необходимость обеспечить более одного пути для трафика j-k, так как, например, очевидно, что если
}. Здесь рассматривается обратная задача – задача распределения потоков(РП) при заданных пропускных способностях, а потоки надо определить так, чтобы минимизировать среднюю задержку. Ранее было отмечено, что допускающие альтернативу процедуры выбора маршрута, дающие более одного пути для трафика j-k оказываются хуже фиксированной процедуры выбора маршрута, в которой предполагается только один путь для этого трафика. Это замечание было основано на предположении, что пропускная способность может быть выбрана так, чтобы удовлетворить требованиям трафика. Здесь рассматривается ситуация, когда пропускные способности заданы, а потоки должны быть оптимально согласованы; поэтому, вероятно, может возникнуть необходимость обеспечить более одного пути для трафика j-k, так как, например, очевидно, что если 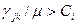 (где
(где 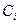 - пропускная способность прямого канала, соединяющего узлы j и k), то требуется более чем один путь для потока j-k.
- пропускная способность прямого канала, соединяющего узлы j и k), то требуется более чем один путь для потока j-k.
В качестве исходного выражения для характеристики 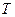 используется
используется
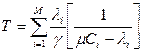 - средняя задержка сообщения в сети.
- средняя задержка сообщения в сети.
То есть требуется минимизировать нелинейную функцию 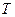 по потокам {
по потокам {  }, чтобы удовлетворились внешние требования к потокам
}, чтобы удовлетворились внешние требования к потокам 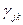 и ограничения на пропускную способность любого канала, состоящие в том, что поток
и ограничения на пропускную способность любого канала, состоящие в том, что поток 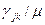 в канале должен быть неотрицательным и меньшим пропускной способности, то есть
в канале должен быть неотрицательным и меньшим пропускной способности, то есть 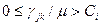 .Это ограничение следует из свойства безграничного возрастания
.Это ограничение следует из свойства безграничного возрастания 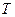 при стремлении какого-либо потока к пропускной способности соответствующего канала. На языке математического программирования это означает, что характеристика
при стремлении какого-либо потока к пропускной способности соответствующего канала. На языке математического программирования это означает, что характеристика 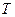 включает дополнительное ограничение на пропускную способность как функцию штрафа. Это важное свойство обеспечивает реализуемость при использовании любого метода минимизации, который представляется в виде последовательности «небольших шагов» и на начальном шаге оперирует с реализуемым решением. Таким образом, если начать с реализации решения, то можно пренебречь ограничением на пропускную способность и вследствие этого задача, которая выглядит как задача с ограничением, фактически будет представлять собой задачу без ограничений. Здесь применима любая разумная процедура поиска. Рассмотрим один из таких методов, предложенный Клейнроком.
включает дополнительное ограничение на пропускную способность как функцию штрафа. Это важное свойство обеспечивает реализуемость при использовании любого метода минимизации, который представляется в виде последовательности «небольших шагов» и на начальном шаге оперирует с реализуемым решением. Таким образом, если начать с реализации решения, то можно пренебречь ограничением на пропускную способность и вследствие этого задача, которая выглядит как задача с ограничением, фактически будет представлять собой задачу без ограничений. Здесь применима любая разумная процедура поиска. Рассмотрим один из таких методов, предложенный Клейнроком.
Из выражения для 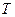 следует, что
следует, что
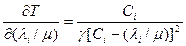 , где
, где 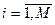
То есть 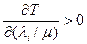 и
и 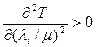 при
при 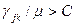 .
.
Отсюда следует, что 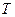 - выпуклая функция. Кроме того, множество реализуемых потоков само является выпуклым многогранником. То есть, если задача имеет реализуемое решение, то любой локальный минимум является глобальным минимумом для
- выпуклая функция. Кроме того, множество реализуемых потоков само является выпуклым многогранником. То есть, если задача имеет реализуемое решение, то любой локальный минимум является глобальным минимумом для 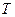 .Следовательно можно использовать любой метод отыскания локального минимума при решении задачи поиска глобального минимума.
.Следовательно можно использовать любой метод отыскания локального минимума при решении задачи поиска глобального минимума.
Метод, применяемый здесь, называется методом отклонения потока (ОП). Он предназначен для поиска глобального минимума. Уясним сначала понятие потока по кротчайшим путям. Предположим, что мы имеем сеть, каждый канал которой имеет надписанную на нем длину 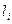 . В такой пути естественно найти кратчайший путь между узлами j и k и попытаться посылать требуемый поток
. В такой пути естественно найти кратчайший путь между узлами j и k и попытаться посылать требуемый поток 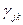 по этому пути(предполагается, что вопросы, связанные с пропускной способностью и задержкой не рассматриваются). Если поступить так для всех (j,k), то в результате получится поток, который называется потоком, идущим по кратчайшим путям. Существует ряд алгоритмов отыскания таких потоков. Один из них следующий.
по этому пути(предполагается, что вопросы, связанные с пропускной способностью и задержкой не рассматриваются). Если поступить так для всех (j,k), то в результате получится поток, который называется потоком, идущим по кратчайшим путям. Существует ряд алгоритмов отыскания таких потоков. Один из них следующий.
Рассмотрим сеть с 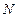 узлами. Пусть
узлами. Пусть 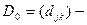 матрица
матрица 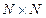 , элемент
, элемент 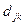 которой дает длину канала, прямо соединяющего узел j с узлом k; если такого канала нет, то этот элемент равен бесконечности(кроме того,
которой дает длину канала, прямо соединяющего узел j с узлом k; если такого канала нет, то этот элемент равен бесконечности(кроме того, 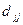 =0). Для пути
=0). Для пути 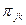 обозначим его длину
обозначим его длину 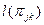 (сумма длин каналов). Задача состоит в вычислении матрицы
(сумма длин каналов). Задача состоит в вычислении матрицы 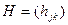 порядка
порядка 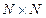 , где
, где 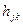 - длина кратчайшего пути, соединяющего узел j и k.Алгоритм начинается с матрицы
- длина кратчайшего пути, соединяющего узел j и k.Алгоритм начинается с матрицы 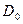 и итеративно изменяет ее, проходя последовательность из
и итеративно изменяет ее, проходя последовательность из 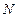 матриц (на n-ом шаге матрица обозначается
матриц (на n-ом шаге матрица обозначается 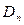 ); в конце он приходит к матрице кратчайших путей
); в конце он приходит к матрице кратчайших путей 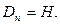
Если начать с n=0 и  ,то
,то 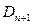 получается
получается 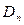 следующим образом (с помощью итерации)):
следующим образом (с помощью итерации)):
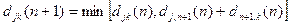 .
.
Для 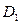 заключаем, что
заключаем, что 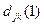 представляет длину кратчайшего пути из узла j в узел k при условии, что допускаются лишь пути с узлом 1 в качестве промежуточного. Аналогично после отыскания
представляет длину кратчайшего пути из узла j в узел k при условии, что допускаются лишь пути с узлом 1 в качестве промежуточного. Аналогично после отыскания 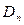 получим, что
получим, что 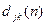 - кратчайшее расстояние от j к узлу k по путям, в которых промежуточные узлы принадлежат множеству {1,2,…n}. Таким образом, дойдя до N итерации, получим искомый результат
- кратчайшее расстояние от j к узлу k по путям, в которых промежуточные узлы принадлежат множеству {1,2,…n}. Таким образом, дойдя до N итерации, получим искомый результат 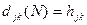 . Весь алгоритм требует
. Весь алгоритм требует 
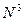 сложений и вычитаний и
сложений и вычитаний и 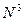 сравнения.
сравнения.
Возвращаясь к исходной задаче сопоставим каждому ребру «длину», которая задается выражением:
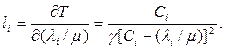
Ясно, что это скорость возрастания  при бесконечно малом увеличении потока
при бесконечно малом увеличении потока 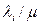 в i-ом канале. Такие «длины» или «стоимостные коэффициенты» могут использоваться для задачи отыскания потоков по кротчайшему маршруту, а полученные пути представляют собой самые дешевые(то есть лучшие для снижения
в i-ом канале. Такие «длины» или «стоимостные коэффициенты» могут использоваться для задачи отыскания потоков по кротчайшему маршруту, а полученные пути представляют собой самые дешевые(то есть лучшие для снижения  ) пути, к которым может быть отклонена(направлена) некоторая часть потока. Вопрос теперь в том, какая часть исходного потока должна быть отклонена.
) пути, к которым может быть отклонена(направлена) некоторая часть потока. Вопрос теперь в том, какая часть исходного потока должна быть отклонена.
После того как она будет определена, можно повторить процесс опять, находя новые длины, определяя новые кратчайшие маршруты и снова отклоняя поток и так далее до тех пор, пока не будет получена приемлемая характеристика. Введем вектор потока на n-ой итерации:
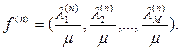
где i-ая компонента 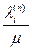 представляет собой полный поток по i-му каналу на n-ой итерации. Будем считать, что начальный поток
представляет собой полный поток по i-му каналу на n-ой итерации. Будем считать, что начальный поток  является реализуемым.
является реализуемым.
ОПТИМАЛЬНЫЙ АЛГОРИТМ ОП ДЛЯ ВЫБОРА МАРШРУТОВ
1. Положить  .
.
2. Для каждого 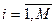 найти
найти
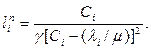
3. Найти 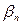 - добавочный стоимостный коэффициент для этого потока:
- добавочный стоимостный коэффициент для этого потока:
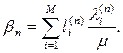
4. Решить задачу отыскания потоков по кратчайшим маршрутам, используя длины  . Пусть
. Пусть 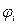 - результирующий поток по i-му каналу, который получается, если весь поток направляется по этим кратчайшим путям. Обозначим вектор потоков через
- результирующий поток по i-му каналу, который получается, если весь поток направляется по этим кратчайшим путям. Обозначим вектор потоков через 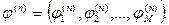
5. Найти 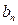 - добавочный стоимостный коэффициент для потока по кратчайшему маршруту:
- добавочный стоимостный коэффициент для потока по кратчайшему маршруту:
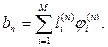
6. (Правило остановки) Если 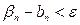 , где
, где 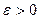 (выбранный допуск), то STOP. В противном случае перейти к п.7.
(выбранный допуск), то STOP. В противном случае перейти к п.7.
7. Найти такое  из интервала
из интервала 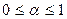 , для которого поток
, для которого поток 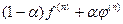 минимизирует
минимизирует  (например, методом Фибоначчи). Оптимальное значение
(например, методом Фибоначчи). Оптимальное значение  обозначим
обозначим 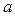 .
.
8. (Отклонение потока). Положить 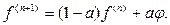
9. Положить 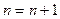 . Перейти к шагу 2.
. Перейти к шагу 2.
Заметим, что отклонение потока производится так, чтобы имело место максимальное снижение значения  . В общем случае это приводит к детерминированной процедуре выбора маршрутов, допускающей альтернативы.
. В общем случае это приводит к детерминированной процедуре выбора маршрутов, допускающей альтернативы.
Метод ОП обеспечивает оптимальный выбор и является сравнительно эффективным с точки зрения вычислений, однако оказалось, что существует более простой подоптимальный метод, который дает фиксированная процедура выбора маршрута и часто приводит к очень хорошим результатам, требуя намного меньше вычислений. Этот метод обходит задачу определения того, какую часть потока нужно отклонит; ОП просто решает, отклонить весь поток или ничего не отклонять для любого 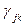 . Приближение основано на сделанном в предыдущем разделе замечании, что фиксированные процедуры выбора маршрута имеют хорошие свойства в смысле коротких средней длины путей и концентрированности трафика. Класс сетей, для которых эффективен такой фиксированный алгоритм выбора маршрута, называется классом больших и сбалансированных сетей. Говорят, что сеть большая, если она имеет большое число узлов, и сбалансирована, если элементы
. Приближение основано на сделанном в предыдущем разделе замечании, что фиксированные процедуры выбора маршрута имеют хорошие свойства в смысле коротких средней длины путей и концентрированности трафика. Класс сетей, для которых эффективен такой фиксированный алгоритм выбора маршрута, называется классом больших и сбалансированных сетей. Говорят, что сеть большая, если она имеет большое число узлов, и сбалансирована, если элементы 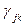 в основном не отличаются друг от друга. В сбалансированной сети вклад трафика j-k в любой канал пренебрежимо мал по сравнению с полным потоком в канале. Если это имеет место, то нетрудно понять, почему рассмотрение фиксированной процедуры выбора маршрутов (отклоняется все или ничего) приводит к хорошему приближению. Опять предположим, что известен начальный реализуемый поток
в основном не отличаются друг от друга. В сбалансированной сети вклад трафика j-k в любой канал пренебрежимо мал по сравнению с полным потоком в канале. Если это имеет место, то нетрудно понять, почему рассмотрение фиксированной процедуры выбора маршрутов (отклоняется все или ничего) приводит к хорошему приближению. Опять предположим, что известен начальный реализуемый поток  , направляемый фиксированной процедурой выбора маршрута.
, направляемый фиксированной процедурой выбора маршрута.
АЛГОРИТМ ОТЫСКАНИЯ ПОТОКОВ, НАПРВЛЯЕМЫХ ФИКСИРОВАННОЙ ПРОЦЕДУРОЙ ВЫБОРА МАРШРУТОВ
1. Положить  .
.
2. Используя поток  , найти множество кратчайших маршрутов
, найти множество кратчайших маршрутов
(по метрике  ).
).
3. Положить 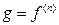 . Для каждого
. Для каждого 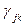 сделать следующие шаги:
сделать следующие шаги:
3а. Пусть 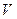 - поток, полученный из
- поток, полученный из 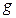 путем отклонения всего потока
путем отклонения всего потока 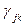 от его пути в потоке
от его пути в потоке  к кратчайшему пути j-k.
к кратчайшему пути j-k.
3б. Если справедливы два утверждения: 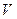 - реализуемый поток и
- реализуемый поток и  , относящееся к
, относящееся к 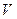 , строго меньше, чем
, строго меньше, чем  для
для 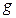 , то перейти к шагу 3в. В противном случае к шагу 3г.
, то перейти к шагу 3в. В противном случае к шагу 3г.
3в. 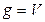 .
.
3г. Если все потоки 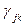 рассмотрены – перейти к шагу 4. В остальных случаях выбрать любой нерассмотренный поток
рассмотрены – перейти к шагу 4. В остальных случаях выбрать любой нерассмотренный поток 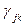 и перейти к 3а.
и перейти к 3а.
4. Если 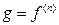 , то STOP: этот метод больше не может улучшить поток. В остальных случаях положить
, то STOP: этот метод больше не может улучшить поток. В остальных случаях положить 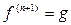 ,
,  и перейти к шагу 2.
и перейти к шагу 2.
Этот алгоритм сходится после конечного числа шагов, так как нужно рассмотреть конечное число потоков 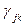 .
.
Заметим, что по результатам моделирования (на сети ARPA) более быстрый подоптимальный алгоритм дает результаты, отклоняющиеся в пределах 2% от результата оптимального алгоритма.


 }. Здесь рассматривается обратная задача – задача распределения потоков(РП) при заданных пропускных способностях, а потоки надо определить так, чтобы минимизировать среднюю задержку. Ранее было отмечено, что допускающие альтернативу процедуры выбора маршрута, дающие более одного пути для трафика j-k оказываются хуже фиксированной процедуры выбора маршрута, в которой предполагается только один путь для этого трафика. Это замечание было основано на предположении, что пропускная способность может быть выбрана так, чтобы удовлетворить требованиям трафика. Здесь рассматривается ситуация, когда пропускные способности заданы, а потоки должны быть оптимально согласованы; поэтому, вероятно, может возникнуть необходимость обеспечить более одного пути для трафика j-k, так как, например, очевидно, что если
}. Здесь рассматривается обратная задача – задача распределения потоков(РП) при заданных пропускных способностях, а потоки надо определить так, чтобы минимизировать среднюю задержку. Ранее было отмечено, что допускающие альтернативу процедуры выбора маршрута, дающие более одного пути для трафика j-k оказываются хуже фиксированной процедуры выбора маршрута, в которой предполагается только один путь для этого трафика. Это замечание было основано на предположении, что пропускная способность может быть выбрана так, чтобы удовлетворить требованиям трафика. Здесь рассматривается ситуация, когда пропускные способности заданы, а потоки должны быть оптимально согласованы; поэтому, вероятно, может возникнуть необходимость обеспечить более одного пути для трафика j-k, так как, например, очевидно, что если 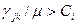 (где
(где 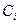 - пропускная способность прямого канала, соединяющего узлы j и k), то требуется более чем один путь для потока j-k.
- пропускная способность прямого канала, соединяющего узлы j и k), то требуется более чем один путь для потока j-k.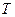 используется
используется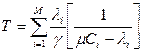 - средняя задержка сообщения в сети.
- средняя задержка сообщения в сети.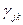 и ограничения на пропускную способность любого канала, состоящие в том, что поток
и ограничения на пропускную способность любого канала, состоящие в том, что поток 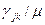 в канале должен быть неотрицательным и меньшим пропускной способности, то есть
в канале должен быть неотрицательным и меньшим пропускной способности, то есть 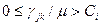 .Это ограничение следует из свойства безграничного возрастания
.Это ограничение следует из свойства безграничного возрастания 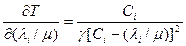 , где
, где 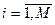
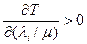 и
и 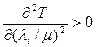 при
при 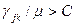 .
.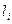 . В такой пути естественно найти кратчайший путь между узлами j и k и попытаться посылать требуемый поток
. В такой пути естественно найти кратчайший путь между узлами j и k и попытаться посылать требуемый поток 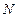 узлами. Пусть
узлами. Пусть 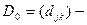 матрица
матрица 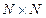 , элемент
, элемент 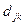 которой дает длину канала, прямо соединяющего узел j с узлом k; если такого канала нет, то этот элемент равен бесконечности(кроме того,
которой дает длину канала, прямо соединяющего узел j с узлом k; если такого канала нет, то этот элемент равен бесконечности(кроме того, 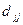 =0). Для пути
=0). Для пути 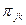 обозначим его длину
обозначим его длину 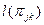 (сумма длин каналов). Задача состоит в вычислении матрицы
(сумма длин каналов). Задача состоит в вычислении матрицы 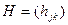 порядка
порядка 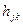 - длина кратчайшего пути, соединяющего узел j и k.Алгоритм начинается с матрицы
- длина кратчайшего пути, соединяющего узел j и k.Алгоритм начинается с матрицы 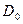 и итеративно изменяет ее, проходя последовательность из
и итеративно изменяет ее, проходя последовательность из 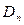 ); в конце он приходит к матрице кратчайших путей
); в конце он приходит к матрице кратчайших путей 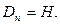
 ,то
,то 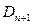 получается
получается 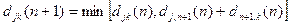 .
.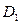 заключаем, что
заключаем, что 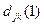 представляет длину кратчайшего пути из узла j в узел k при условии, что допускаются лишь пути с узлом 1 в качестве промежуточного. Аналогично после отыскания
представляет длину кратчайшего пути из узла j в узел k при условии, что допускаются лишь пути с узлом 1 в качестве промежуточного. Аналогично после отыскания 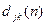 - кратчайшее расстояние от j к узлу k по путям, в которых промежуточные узлы принадлежат множеству {1,2,…n}. Таким образом, дойдя до N итерации, получим искомый результат
- кратчайшее расстояние от j к узлу k по путям, в которых промежуточные узлы принадлежат множеству {1,2,…n}. Таким образом, дойдя до N итерации, получим искомый результат 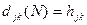 . Весь алгоритм требует
. Весь алгоритм требует 
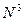 сложений и вычитаний и
сложений и вычитаний и 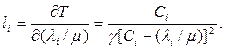
 при бесконечно малом увеличении потока
при бесконечно малом увеличении потока 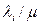 в i-ом канале. Такие «длины» или «стоимостные коэффициенты» могут использоваться для задачи отыскания потоков по кротчайшему маршруту, а полученные пути представляют собой самые дешевые(то есть лучшие для снижения
в i-ом канале. Такие «длины» или «стоимостные коэффициенты» могут использоваться для задачи отыскания потоков по кротчайшему маршруту, а полученные пути представляют собой самые дешевые(то есть лучшие для снижения 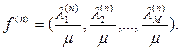
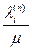 представляет собой полный поток по i-му каналу на n-ой итерации. Будем считать, что начальный поток
представляет собой полный поток по i-му каналу на n-ой итерации. Будем считать, что начальный поток  является реализуемым.
является реализуемым. .
.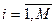 найти
найти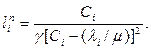
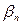 - добавочный стоимостный коэффициент для этого потока:
- добавочный стоимостный коэффициент для этого потока: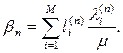
 . Пусть
. Пусть 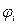 - результирующий поток по i-му каналу, который получается, если весь поток направляется по этим кратчайшим путям. Обозначим вектор потоков через
- результирующий поток по i-му каналу, который получается, если весь поток направляется по этим кратчайшим путям. Обозначим вектор потоков через 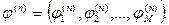
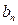 - добавочный стоимостный коэффициент для потока по кратчайшему маршруту:
- добавочный стоимостный коэффициент для потока по кратчайшему маршруту: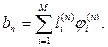
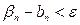 , где
, где 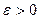 (выбранный допуск), то STOP. В противном случае перейти к п.7.
(выбранный допуск), то STOP. В противном случае перейти к п.7. из интервала
из интервала 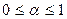 , для которого поток
, для которого поток 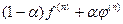 минимизирует
минимизирует 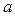 .
.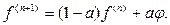
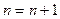 . Перейти к шагу 2.
. Перейти к шагу 2.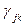 . Приближение основано на сделанном в предыдущем разделе замечании, что фиксированные процедуры выбора маршрута имеют хорошие свойства в смысле коротких средней длины путей и концентрированности трафика. Класс сетей, для которых эффективен такой фиксированный алгоритм выбора маршрута, называется классом больших и сбалансированных сетей. Говорят, что сеть большая, если она имеет большое число узлов, и сбалансирована, если элементы
. Приближение основано на сделанном в предыдущем разделе замечании, что фиксированные процедуры выбора маршрута имеют хорошие свойства в смысле коротких средней длины путей и концентрированности трафика. Класс сетей, для которых эффективен такой фиксированный алгоритм выбора маршрута, называется классом больших и сбалансированных сетей. Говорят, что сеть большая, если она имеет большое число узлов, и сбалансирована, если элементы  , найти множество кратчайших маршрутов
, найти множество кратчайших маршрутов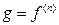 . Для каждого
. Для каждого 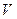 - поток, полученный из
- поток, полученный из 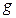 путем отклонения всего потока
путем отклонения всего потока 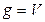 .
.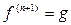 ,
,  и перейти к шагу 2.
и перейти к шагу 2.


