
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача выбора пропускных способностей.
Эта задача, усложняется тем, что оптимальный вектор пропускных способностей необходимо делать из конечного набора их возможных значений, то есть задача целочисленного программирования, решается она численными методами аналитического решения в замкнутой форме не имеет. Поэтому будем считать (для теоретического изучения), что пропускная способность выбирается из непрерывного ряда. Считаем, что известна топология и потоки {
где Для минимизации
Отсюда
Найдем
Откуда
Обозначим тогда
Это и есть оптимальное решение задачи ВПС. При таком наборе пропускная способность любого канала будет иметь по крайней мере пропускная способность Как следует из (9) эта добавочная стоимость сначала нормируется коэффициентом Если подставить (9) в выражение для
Это равенство – минимальная средняя задержка в сети, пропускные способности в которой выбраны оптимально. При
Рассмотрим частный случай имеют вид:
где т.е.
Величина Отметим, что Другая сеть, в которой также имеется один входной и один выходной канал за исключением центрального узла, является звездообразной(см.рис 9).
Рис.10. Звездообразная сеть.
Здесь средняя длина пути
Показано, что выбор зависит от Полученные выше выводы относились к фиксированному процессу выбора маршрута. Даст ли улучшение использование процесса выбора маршрута, допускающего альтернативы? Такая процедура предлагает более чем 1 путь и, кроме того, она дает упорядочение по предпочтению этих путей – обычно длинные пути менее предпочтительны, чем прямые. Поэтому допускающие альтернативу процедуры выбора маршрута приводят к увеличению длины пути, и, в то же время, они пытаются распределить поток по многим каналам, а не концентрировать его лишь на нескольких каналах. При допускающей альтернативы процедуре нарушаются оба интуитивных правила, выведенные выше. Результаты моделирования показывают, что следует отказать предпочтение последовательности указанных выше топологий и что фиксированные процедуры выбора маршрута оказываются лучше процедур, допускающих альтернативы. Эти результаты получены в предположении, что величины Было заключено, что при линейной стоимостной функции, при минимизации
Выбор этой функции обусловлен тем, что большие значения Решая эту задачу как прежде, получим
. При
Отметим, что все При
В этом случае пропускная способность прямо пропорциональна (при Более интересно то, что величина
Контрольные вопросы: 1.Какое оптимальное значение пропускной способности канала в задаче ВПС? 2. Какое оптимальное значение средней задержки в сети? 3.Охарактеризуйте фиксированную процедуру выбора маршрута. 4.Охарактеризуйте процедуру выбора маршрута, допускающую альтернативы. 5. Какая величина называется пропорциональным набором пропускным способностей? 6. Что такое полносвязная сеть? 7. Чему равна средняя длина пути в сети? 8. При каких значениях ρ оптимальной топологией является полносвязная сеть?
Лекция №5
|
|||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 216; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.114.125 (0.019 с.) |
 }. Заметим, что
}. Заметим, что 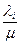 - есть среднее число битов в секунду, которые проходят по i-му каналу, и, следовательно, любое реализуемое решение задачи ВПС должно быть таким, чтобы i-ый канал имел пропускную способность не меньшую указанной величины, то есть чтобы
- есть среднее число битов в секунду, которые проходят по i-му каналу, и, следовательно, любое реализуемое решение задачи ВПС должно быть таким, чтобы i-ый канал имел пропускную способность не меньшую указанной величины, то есть чтобы 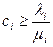 . Рассмотрение будем вести для линейных стоимостных функций, то есть
. Рассмотрение будем вести для линейных стоимостных функций, то есть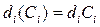 ,
,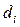 - стоимость в расчете на единицу пропускной способности i-го канала.
- стоимость в расчете на единицу пропускной способности i-го канала. 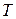 составим функцию Лагранжа.
составим функцию Лагранжа.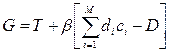 ,где
,где 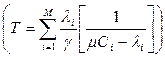
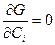 ; что дает
; что дает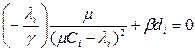 или
или .
.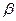 , умножив последнее равенство на
, умножив последнее равенство на 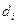 и, просуммировав по i, получим:
и, просуммировав по i, получим: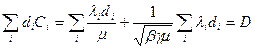
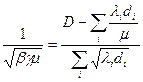 .
.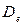

 (9),
(9),
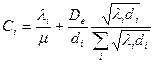 (10)
(10)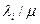 (то есть минимально требуемое значение) и, кроме того, некоторая дополнительная пропускная способность. Отметим, что стоимость минимальной пропускной способности i-го канала равна
(то есть минимально требуемое значение) и, кроме того, некоторая дополнительная пропускная способность. Отметим, что стоимость минимальной пропускной способности i-го канала равна  ; взяв сумму по всем каналам, получим допустимую стоимость. Разность между полной стоимостью и минимально допустимой стоимостью равна
; взяв сумму по всем каналам, получим допустимую стоимость. Разность между полной стоимостью и минимально допустимой стоимостью равна 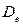 и задается (9). Поэтому
и задается (9). Поэтому  и затем распределяется по всем каналам пропорционально квадратному корню из взвешенной интенсивности потока
и затем распределяется по всем каналам пропорционально квадратному корню из взвешенной интенсивности потока 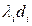 . Такой оптимальный набор пропускных способностей называется набором пропускных способностей по закону квадратного корня.
. Такой оптимальный набор пропускных способностей называется набором пропускных способностей по закону квадратного корня.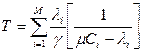 , то получим:
, то получим:
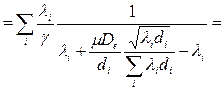

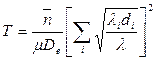 , где
, где 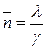 (11)
(11)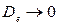 ,
, 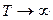 . Если
. Если  задача ВПС имеет реализуемое (осуществимое) решение(то есть
задача ВПС имеет реализуемое (осуществимое) решение(то есть 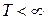 ). Если
). Если 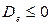 задача не имеет реализуемого решения. Уравнения (10) и (11) дают полное решение ВПС.
задача не имеет реализуемого решения. Уравнения (10) и (11) дают полное решение ВПС.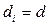 , при этом, не теряя общности, можно положить d=1. Этот случай имеет место при рассмотрении спутниковых каналов связи, в которых расстояние между двумя различными точками(на Земле, та как логический канал – это узел-узел) в зоне спутника по существу является одинаковым независимо от расстояния между этими точками на поверхности земли. Здесь Если
, при этом, не теряя общности, можно положить d=1. Этот случай имеет место при рассмотрении спутниковых каналов связи, в которых расстояние между двумя различными точками(на Земле, та как логический канал – это узел-узел) в зоне спутника по существу является одинаковым независимо от расстояния между этими точками на поверхности земли. Здесь Если  , то есть сумма всех пропускных способностей сети, которые обозначим как
, то есть сумма всех пропускных способностей сети, которые обозначим как 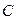 . Тогда выражения для
. Тогда выражения для 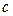 и
и 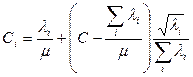
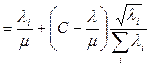
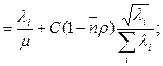
 (это не коэффициент использования, просто совпадают обозначения),
(это не коэффициент использования, просто совпадают обозначения), 
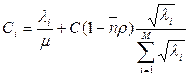 (12)
(12) 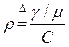
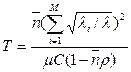 (13)
(13)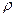 введена потому, что она является заданной величиной.
введена потому, что она является заданной величиной.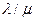 (средней скорости, с которой биты входят в сеть от внешних источников) к C(суммарной пропускной способности сети).
(средней скорости, с которой биты входят в сеть от внешних источников) к C(суммарной пропускной способности сети).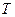 является строго возрастающей функцией от
является строго возрастающей функцией от  .Это наводит на мысль, что топологию структуры сети, видимо, следует выбирать так, чтобы получить минимальную среднюю длину. Последнее достигается в полносвязной сети(любая пара узлов связана каналом). Кроме того, если рассмотреть сумму в числителе
.Это наводит на мысль, что топологию структуры сети, видимо, следует выбирать так, чтобы получить минимальную среднюю длину. Последнее достигается в полносвязной сети(любая пара узлов связана каналом). Кроме того, если рассмотреть сумму в числителе 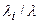 }, когда одна из этих величин равна единице, а остальную сумму в числителе нельзя минимизировать таким образом, так как при этом весь поток будет идти по одному каналу, а остальные будут простаивать. Однако суммирование подсказывает, что нужно посылать большую часть потока по нескольким скоростным каналам и лишь малую часть – по остальным каналам. Обычно для связи требуется по крайней мере один входящий и один выходящий канал для любого узла. Такая сеть представляет собой кольцо, но здесь большая средняя длина пути.
}, когда одна из этих величин равна единице, а остальную сумму в числителе нельзя минимизировать таким образом, так как при этом весь поток будет идти по одному каналу, а остальные будут простаивать. Однако суммирование подсказывает, что нужно посылать большую часть потока по нескольким скоростным каналам и лишь малую часть – по остальным каналам. Обычно для связи требуется по крайней мере один входящий и один выходящий канал для любого узла. Такая сеть представляет собой кольцо, но здесь большая средняя длина пути.
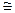 2. Теперь следует сделать выбор между полной сетью, звездообразной сетью и всеми остальными промежуточными меду ними.
2. Теперь следует сделать выбор между полной сетью, звездообразной сетью и всеми остальными промежуточными меду ними.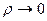 наиболее подходящей является звезда, а при
наиболее подходящей является звезда, а при 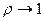 - полносвязная сеть. Можно ожидать, что между этими двумя экстремальными топологиями приемлемую топологию даст добавление некоторых прямых каналов к звездообразной сети.
- полносвязная сеть. Можно ожидать, что между этими двумя экстремальными топологиями приемлемую топологию даст добавление некоторых прямых каналов к звездообразной сети. известны и постоянны. Если же они либо неизвестны, либо меняются, либо и то, и другое, то из
известны и постоянны. Если же они либо неизвестны, либо меняются, либо и то, и другое, то из 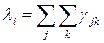 , где
, где 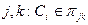 , нельзя найти параметры потока в каналах
, нельзя найти параметры потока в каналах 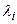 и, следовательно, оптимальное распределение потока с помощью равенств типа (7). Таким образом, в некоторые периоды времени сеть не будет оптимизированной. Если рассогласование велико, то необходимо введение адаптивной, допускающей альтернативы процедуры для недогруженных путей во время этих интервалов.
и, следовательно, оптимальное распределение потока с помощью равенств типа (7). Таким образом, в некоторые периоды времени сеть не будет оптимизированной. Если рассогласование велико, то необходимо введение адаптивной, допускающей альтернативы процедуры для недогруженных путей во время этих интервалов. .В результате была поставлена новая задача ВПС, в которой следует минимизировать функцию:
.В результате была поставлена новая задача ВПС, в которой следует минимизировать функцию: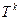

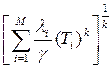
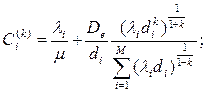
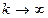 имеем:
имеем: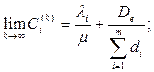
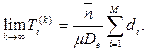
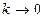 получим:
получим: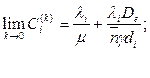
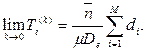
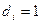 ) интенсивности потоков
) интенсивности потоков 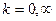 ), хотя наборы пропускных способностей очень отличаются.
), хотя наборы пропускных способностей очень отличаются.


