Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розрахунково-графічне завдання № 7Содержание книги Поиск на нашем сайте
Тема. Операторний метод розрахунку перехідних процесів Мета: розрахунок перехідних процесів в електричних колах з двома реактивними елементами за допомогою операторного методу.
Короткі теоретичні відомості Алгоритм розрахунку: 1. Знаходження незалежних початкових умов (НПУ) iL(0-), uC(0-) – за аналогією з класичним методом. 2. Складання операторної схеми заміщення (схема після комутації). Змін зазнають реактивні елементи; залежно від конфігурації кола використовують послідовну чи паралельну схеми заміщення.
3. Вираження невідомої величини як L – зображення F(p). 4. Відтворення ориґіналу, як функції часу: F(p) Найчастіше ця величина має вигляд дробу Якщо F(p) задовольняє вищезгадані вимоги, то для відтворення функції часу можна користуватись таким алгоритмом: 4.1 Знайти корені знаменника дробу з рівняння N(p) = 0 (вони повинні співпадати з коренями характеристичного рівняння класичного методу): p1, p2, …pk,…pn. 4.2 Залежно від виду коренів записують ориґінал за допомогою теореми розкладання. Наведемо окремі випадки: – корені дійсні та різні (приклад 7.1):
– є один нульовий корінь p = 0 і n ненульових p1, p2, …pk,…pn, тоді дріб можна зобразити у вигляді:
– корені комплексно-спряжені
де pk – один із пари комплексно-спряжених коренів, наприклад Приклад 7.1 Записати ориґінал виразу
Розв’язання Отже, маємо відношення поліномів Степінь чисельника більший за степінь знаменника, то можливо скористатися алгоритмом, наведеним у п. 4. Знайдемо корені рівняння знаменника: Маємо: Тому функція часу буде мати вигляд:
Приклад 7.2 Записати ориґінал виразу Розв’язання Очевидно, що в знаменнику є нульовий корінь:
отже, маємо корені: Тоді поліноми будуть мати вигляд: Запишемо функцію часу:
Приклад 7.3 Записати ориґінал виразу Розв’язання Знайдемо корені рівняння знаменника: Дискримінант: Маємо: Вирази, необхідні для запису функції часу:
Приклад 7.4 Для кола, зображеного на рис. 7.2, а, знайти струм iL(t), якщо відомі параметри кола: I0 = 1 А, R = 100 Ом, C = 5 мкФ, L = 40 мГн.
а) б) Рисунок 7.2 – Вихідне коло до розрахунку (а) та схема кола до комутації в сталому режимі (б) Розв’язання 1. Знайдемо НПУ. За аналогією з класичним методом (див. приклад 6.1): iL(0-) = 0; uC(0-) = uR =I0·R = 100 В. 2. Складемо операторну схему заміщення (схема після комутації).
Рисунок 7.3 – Операторна схема заміщення Об’єднаємо три джерела струму в одне, як показано на рис. 7.4, де струм об’єднаного джерела:
Рисунок 7.4 – Схема після перетворення Знайдемо струм IL(p):
Знаменник З урахуванням нульового кореня: Розпишемо всі складові виразу:
Після підстановки маємо:
Вираз у квадратних дужках переведемо до показникової форми запису:
Остаточно:
Приклад 7.5 Для кола, зображеного на рис. 7.5, знайти струм iL(t), якщо відомі параметри кола: U = 10 B, R = 10 Ом, C = 250 мкФ, L = 4 мГн.
Рисунок 7.5 – Схема для розв’язання
Розв’язання Спочатку оберемо додатні напрямки струмів у гілках схеми. 1. НПУ знайдемо зі схеми до перемикання ключа. У зв’язку з тим, що котушка від’єднана від джерела, маємо: iL(0-) = 0; uC(0-) = U0 = 10 В. 2. Складемо операторну схему заміщення для схеми після комутації рис. 7.6. У цьому випадку зручно користуватись послідовними схемами заміщення реактивних елементів (рис. 7.6, б).
Об’єднаємо два джерела напруги в одне, як показано на рис. 7.6, в, де напруга об’єднаного джерела:
Знайдемо струм IL(p):
4. Розв’яжемо рівняння:
Маємо корені: Корені реальні та різні – тому функція часу буде мати вигляд:
Завдання до теми Виконати розрахунки попереднього завдання 6 за допомогою операторного методу. Порівняти одержані результати з розрахунками за класичним методом. Контрольні питання 1. Наведіть алгоритм аналізу перехідного процесу операторним методом. 2. Запишіть формули переходу від L-зображень до функцій часу при: а) дійсних і різних коренях характеристичного рівняння (нульового кореня немає); б) дійсних і різних коренях характеристичного рівняння (є нульовий корінь); в) комплексно-спряжених коренях. Література: [1–4].
|
||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 101; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.143.118 (0.005 с.) |


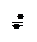 f(p).
f(p).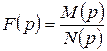 , де M(p) та N(p) – поліноми, причому ступінь чисельника повинен бути більший за степінь знаменника.
, де M(p) та N(p) – поліноми, причому ступінь чисельника повинен бути більший за степінь знаменника.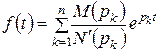 ,
,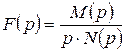 (приклад 7.2):
(приклад 7.2):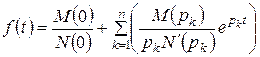 ,
,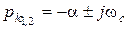 (приклад 7.3):
(приклад 7.3):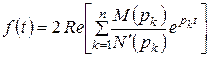 ,
,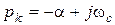 .
.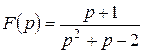 .
.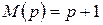 та
та 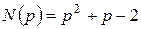 .
.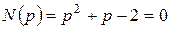 .
.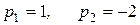 – корені дійсні та різні.
– корені дійсні та різні.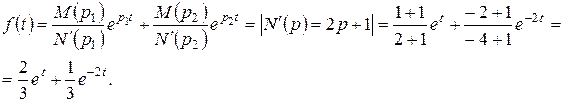
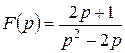 .
.
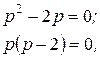
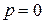 ,
, 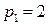 .
.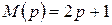 та
та 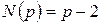 .
.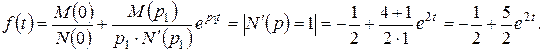
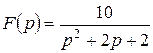 .
.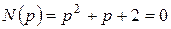 .
.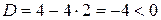
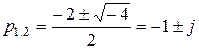 – корені комплексно-спряжені.
– корені комплексно-спряжені. ,
, 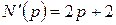 , та після підстановки кореня:
, та після підстановки кореня: 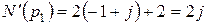 .
.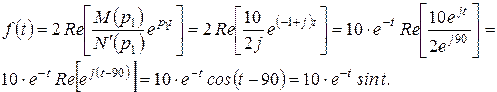

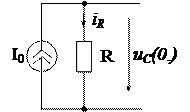

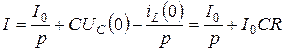 .
.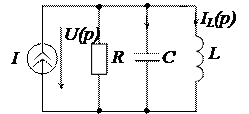
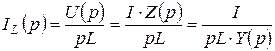 ;
;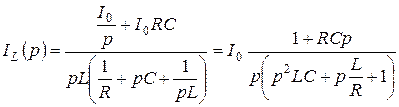 .
.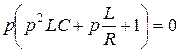 має три корені:
має три корені: 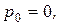
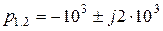
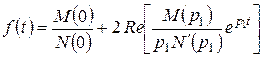 .
.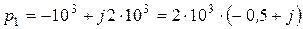 ;
;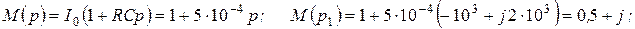
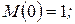
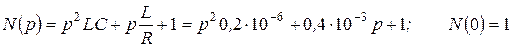 ;
;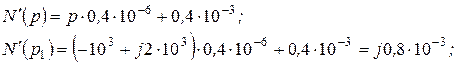
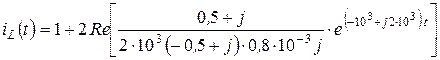 .
.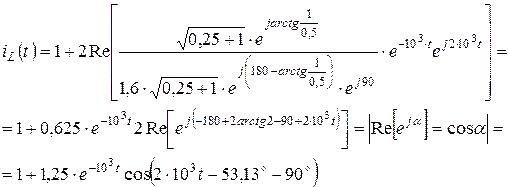
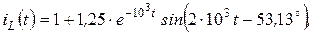 А
А

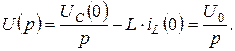
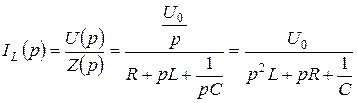 .
.