
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Максимуми і мінімуми функції ⇐ ПредыдущаяСтр 2 из 2
Означення 1. Функція y=f(x) має максимум в точці х0, якщо значення функції в деякому околі цієї точки не перевищують значення в самій точці, тобто ¦(х)£¦(х0). Означення 2. Функція y=f(x) має мінімум в точці х1, якщо значення функції в деякому околі цієї точки не менші значення в самій точці, тобто ¦(х)³¦(х1).
рис.42 Максимуми і мінімуми функції називають екстремуми. Функція y=f(x) може мати на даному відрізку декілька максимумів і мінімумів. Екстремуми мають локальний (місцевий) характер, вони описують поведінку функції тільки в околі даної точки. Всі точки, в яких функція набуває екстремума називається критичними. Наприклад. На рисунку 42 точки x0,x1,x2,x3 – критичні точки. Теорема 1. (Необхідна умова екстремума). Якщо функція y=f(x) має екстремум при х=х0, то похідна в цій точці, якщо вона існує, дорівнює нулю, тобто ¦¢(х0)=0. Наприклад. На рис.1 ¦¢(х0)=¦¢(х1)=¦¢(х2)=0. Теорема 1 виражає тільки необхідну умову екстремума, але не достатню, див. рис. 43
0 x0 X рис.43 Точки в яких ¦¢(х0)=0 називаються стаціонарними, в них швидкість зміни функції дорівнює нулю. Із викладеного випливає, що критичні точки функції, тобто точки екстремума, слідує шукати серед стаціонарних точок, де ¦¢(х0)=0, також серед точок, в яких похідна ¦¢(х) не існує. Наприклад в точці х3 (рис.42) функція має мінімум, але графік не є гладким, похідна в точці х3 – не існує. Теорема 2. (Достатня умова екстремуму). Нехай функція у=¦(х): 1) неперервна при х=х0; 2) має похідну ¦¢(х0) в деякому околі точки х0, за винятком, можливо, самої цієї точки; 3) похідна зберігає знак окремо зліва і справа від х0. Тоді, якщо при переході через точку х0 (зліва направо) а) ¦¢(х) змінює знак з “+” на “–”, то при х=х0 маємо максимум; б) ¦¢(х) змінює знак з “–” на “+”, то при х=х0 маємо мінімум; в) якщо знак похідної не змінюється, то в точці х0 екстремуму не має. Теорема 3. (Друга достатня умова екстремуму). Якщо функція у=¦(х) в точці х=х0 має першу і другу похідну, причому ¦¢(х0)=0, а ¦¢¢(х0)¹0, і ¦¢¢(х) неперервна в околі точки х=х0, то в точці х=х0 у=¦(х) має екстремум, причому це буде максимум, якщо ¦¢¢(х0)<0, і мінімум, якщо ¦¢¢(х0)>0. Див., напр., рис. 44
Y
x0 x1 X рис.44 Скорочено маємо:
Можуть зустрічатись випадки, коли ¦¢(х0)=0 і ¦¢¢(х0)=0, тоді користуються більш загальним твердженням. Теорема 4. Якщо функція у=¦(х) має в околі точки х=х0 неперервні похідні до n-го порядку (n>1) включно і якщо
в той час як f(n)(x0)¹0, то при n парному функція має максимум, якщо f(n)(x0)<0, i мінімум, якщо f(n)(x0)>0; якщо n – непарне, то функція екстремума в точці х=х0 не має. Приклади. Дослідити на екстремуми функції: 1. Розв’язання 1. 1) Спочатку скористаємось необхідною умовою екстремума, прирівнявши до нуля першу похідну,
В даному прикладі точки розриву похідної відсутні. 2) Наносимо нулі і точки розриву похідної на числову вісь, яка розбивається при цьому на інтервали
3) Методом проб відшукуємо інтервали монотонності функції за знаками похідної. В даному випадку: Якщо Якщо Якщо ж Тут 4) Перевіримо достатню умову екстремума, а саме, якщо при переході в напряму осі з “-“ на “+”, то в точці з “+” на “-“, то в точці У даному прикладі при переході через
При переході через точку
Відповідь: 2. Знаходимо похідну
Похідна не існує в точці
на на на на У точках
Задача. По кожному з кутів квадратного листа картону, сторона якого 60 см, вирізають однакові квадратики і відкидають їх. З матеріалу, що залишився, згинають картон так, щоб утворились бічні грані коробки без кришки. Яка повинна бути довжина сторони вирізуваного квадратика, щоб після склеювання отримати коробку максимального об’єму? Знайти цей об’єм.
Позначимо через
Висота коробки -
Рис. Функцію
Знаходимо похідну
Прирівняємо похідну до нуля
Дослідимо знаки похідної.
Отже, при
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 544; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.184.214 (0.017 с.) |


 f(x2)=ymax
f(x2)=ymax

 Y f(x0)=ymax
Y f(x0)=ymax
 f(x3)=ymin
f(x3)=ymin
 f(x1)=ymin
f(x1)=ymin x0 x1 x2 x3 X
x0 x1 x2 x3 X
 Y
Y ¦¢(х0)=0 y=f(x)
¦¢(х0)=0 y=f(x)
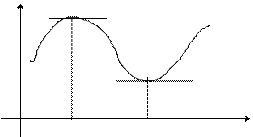


 . 2.
. 2.  .
. . Звідки знайдемо стаціонарні точки. Знаходимо також точки розриву похідної, якщо такі є.
. Звідки знайдемо стаціонарні точки. Знаходимо також точки розриву похідної, якщо такі є. .
.
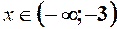 , то із
, то із  маємо
маємо  , функція
, функція  - зростає;
- зростає; , то із
, то із  функція
функція  - спадає;
- спадає; , то
, то  , функція
, функція  - зростає.
- зростає. - пробні точки з відповідних інтегралів.
- пробні точки з відповідних інтегралів. через точку
через точку  похідна міняє знак
похідна міняє знак ,
, .
.
 міняє знак з “+” на “-“. Отже, у точці
міняє знак з “+” на “-“. Отже, у точці  .
. в напрямку осі
в напрямку осі  .
. .
.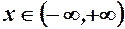 .
. .
. і має нулі в точках
і має нулі в точках  ,
, 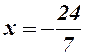 . Наносимо їх на числову вісь і отримуємо інтервали
. Наносимо їх на числову вісь і отримуємо інтервали
 - ф. зростає;
- ф. зростає;
 - ф. зростає;
- ф. зростає; - ф. спадає;
- ф. спадає; - ф. зростає.
- ф. зростає.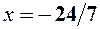 і
і  похідна міняє знак, значить то є екстремум, причому в точці
похідна міняє знак, значить то є екстремум, причому в точці  ;
; .
. довжину сторони одного з чотирьох вирізуваних квадратиків, які відкидаються. На рисунку вони заштриховані. По пунктирних лініях робиться згин частин картону. Дно коробки – це квадрат зі стороною довжини
довжину сторони одного з чотирьох вирізуваних квадратиків, які відкидаються. На рисунку вони заштриховані. По пунктирних лініях робиться згин частин картону. Дно коробки – це квадрат зі стороною довжини  . Площа дна
. Площа дна ,
,

 дослідимо на екстремум, спростивши її
дослідимо на екстремум, спростивши її .
.
 .
. .
.
 об’єм досягає максимуму.
об’єм досягає максимуму.



