
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Додавання і віднімання комплексних чисел в алгебраїчній форміСодержание книги
Поиск на нашем сайте
Розглянемо два комплексні числа Сумою двох векторів є вектор
Рис. 3 Рис. 4 Проекції вектора суми векторів
Вектору суми
Формула, аналогічна формулі (4), має місце і при додаванні будь-якої скінченої кількості комплексних чисел:
При додаванні комплексних чисел в алгебраїчній формі окремо додаються дійсні частини комплексних чисел і окремо уявні частини.
Повернемося до запису комплексного числа. Тепер комплексне число
Отже, комплексне число — це сума дійсного числа Таким чином, маємо алгебраїчну форму комплексного числа
де Приклад. Нехай
Дію віднімання двох комплексних чисел розглядаємо як дію, обернену до дії додавання. Нехай
Тоді
Два комплексні числа рівні між собою, якщо рівні між собою дійсна і уявна частини цих чисел, тобто
3.1. Cпряженi комплекснi числа Комплексне число
Задане комплексне число і спряжене до нього розташовані симетрично відносно осі
Так, спряженими до чисел
Рис. 5 будуть числа
3.1.1. Властивості спряжених комплексних чисел
Для спряжених комплексних чисел справедливе твердження: 1. Комплексне число, спряжене до суми комплексних чисел, дорівнює сумі спряжених чисел:
Доведення. Cума комплексних чисел
Спряжене комплексне число до цієї суми має вигляд
З іншої сторони, cума спряжених комплексних чисел дорівнює
Порівнюючи останні рівності, бачимо, що твердження (8) справджується. Приклад. Знайти спряжене число до суми чисел Розв’язання. Знаходимо суму заданих чисел за формулою (4):
3.1.2. Мають місце також наступні твердження, які легко перевірити. А саме, · сума комплексного числа і спряженого до нього є дійсне число · різниця комплексного числа і спряженого до нього є суто уявне число Доведення. Маємо
|
||||
|
Последнее изменение этой страницы: 2017-01-18; просмотров: 328; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.28.213 (0.006 с.) |

 та
та  . Їм відповідають вектори
. Їм відповідають вектори  та
та  .
.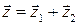 , що з’єднує початок першого вектора
, що з’єднує початок першого вектора 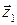 з кінцем другого вектора
з кінцем другого вектора  , якщо другий вектор бере свій початок в кінці першого вектора (рис. 3).
, якщо другий вектор бере свій початок в кінці першого вектора (рис. 3).

 .
. векторів
векторів 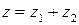 — сума комплексних чисел
— сума комплексних чисел  . (4)
. (4) .
. можна записати як суму двох комплексних чисел — дійсного числа
можна записати як суму двох комплексних чисел — дійсного числа  і суто уявного числа
і суто уявного числа  :
: .
. у записі
у записі  надалі розглядається як знак додавання.
надалі розглядається як знак додавання.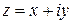 , (5)
, (5) . При цьому в алгебраїчній формі комплексного числа (5) завжди має стояти знак
. При цьому в алгебраїчній формі комплексного числа (5) завжди має стояти знак 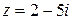 . Тут
. Тут  і алгебраїчна форма цього числа має вигляд:
і алгебраїчна форма цього числа має вигляд: 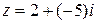
 , де
, де 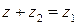 . Згідно з означенням дії додавання маємо
. Згідно з означенням дії додавання маємо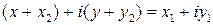 .
. . Звідки
. Звідки  . Отже, різницю комплексних чисел знаходимо за формулою
. Отже, різницю комплексних чисел знаходимо за формулою . (6)
. (6) називається спряженим до комплексного числа
називається спряженим до комплексного числа 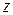 , якщо в алгебраїчній формі комплексного числа
, якщо в алгебраїчній формі комплексного числа  замінити
замінити 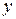 на
на  , тобто
, тобто або
або 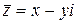 . (7)
. (7) (рис. 5).
(рис. 5).

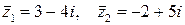 .
. . (8)
. (8) .
. .
.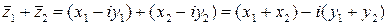 .
.
 . Згідно з означенням спряженого комплексного числа дістаємо, що
. Згідно з означенням спряженого комплексного числа дістаємо, що  .
.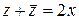 .
. .
. ,
,  , тобто дійсно твердження мають місце
, тобто дійсно твердження мають місце


