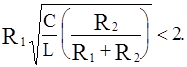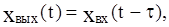Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Форсирующее (идеальное) звено.Содержание книги Поиск на нашем сайте
Часто в литературе именуется как пропорционально-дифференцирующее. Выходная величина этого звена пропорциональна входной и производной от входной величины. Передаточная функция и основные частотные функции:
Звено характеризуется двумя параметрами-коэффициентом передачи k и постоянной дифференцирования t. В начальный момент времени переходная характеристика, как и у идеального дифференцирующего звена, должна иметь скачек бесконечной амплитуды. ЛФЧХ форсирующего звена точно такая же, как и у апериодического, только фаза имеет положительные значения. Низкочастотные асимптоты ЛАЧХ форсирующего и апериодического звеньев совпадают, но высокочастотная асимптота ЛАЧХ форсирующего звена имеет наклон плюс 20 дБ/дек. Сопрягающая частота
G(w) j(w)
Рис. 2.16
Звенья второго порядка. В общем случае описываются уравнением
Перейдем к изображениям по Лапласу:
Отсюда определяем передаточную функцию:
Однако общепринята запись передаточной функции звеньев второго порядка в другом виде:
где Звенья второго порядка, таким образом, характеризуются тремя параметрами. Это коэффициент передачи, постоянная времени и коэффициент демпфирования x. В зависимости от величины коэффициента демпфирования различают типы звеньев: колебательное (0<x<1), консервативное (x=0) и апериодическое второго порядка (x³1). Рассмотрим свойства колебательного звена. Выражения для его частотных функций имеют следующий вид:
Асимптотическая ЛАЧХ строится тем же приемом, что и для апериодического звена. В области низких частот Tw<<1 и в подкоренном выражении всеми членами, кроме 1, можно пренебречь. Тогда низкочастотная асимптота G(w)нч принимает вид G(w)нч»20lgk. В области высоких частот G(w)вч»20lgk-20lg(Tw)2=20lgk-40lgTw. Эта асимптота имеет наклон минус 40 дБ/дек. Сопрягаются асимптоты на частоте
Асимптотическая ЛАЧХ 20lgk -40 дБ/дек
0 lgw
j(w) Рис.2.17
Точная ЛАЧХ
В районе Представление о динамических свойствах звена можно получить из переходной характеристики, представленной на рис.2.18.
h(t)
  
Рис.2.18
Примером звена второго порядка может служить колебательный контур (см. схему на рис.2.5 и вывод передаточной функции в примере 2.4). Консервативное звено - частный случай колебательного звена, когда отсутствует демпфирование. Если обратиться к приведенному выше примеру (см. рис.2.5), то должны отсутствовать потери в контуре (выполняться условие R=0). В этом случае колебания стали бы незатухающими, и переходная характеристика описывалась бы выражением:
На сопрягающей частоте ЛАЧХ консервативного звена имеет всплеск бесконечной амплитуды, т.е. претерпевает разрыв, а ЛФЧХ из нулевого значения скачком достигает значения минус p. При x ³ 1 передаточную функцию звена второго порядка можно преобразовать следующим образом:
где То есть апериодическое звено второго порядка не является типовым или элементарным, так как его можно представить двумя последовательно соединенными более простыми звеньями - апериодическими первого порядка. Пример 2.7. Определить, при каком соотношении параметров элементов схемы колебательный контур (см. рис.2.5) является колебательным звеном. Запишем полученную в примере 2.4 передаточную функцию с использованием коэффициента демпфирования:
Отсюда выразим коэффициент демпфирования:
Звено будет колебательным, если z<1, т.е.
В противном случае, т.е. при
контур будет являться апериодическим звеном второго порядка. При этом следует обратить внимание на то, что лишь с позиций математического описания схему можно представить как последовательное соединение двух апериодических звеньев первого порядка. Расчленить же принципиальную схему на два участка, каждый из которых был бы соответствующим апериодическим звеном первого порядка, невозможно.
Звено чистого запаздывания. Это звено без искажения воспроизводит на выходе входную величину, как идеальное пропорциональное звено, но с той разницей, что выходная величина запаздывает относительно входной на постоянное время. Уравнение такого звена имеет вид:
где t - время запаздывания. Очевидно, характеристики этого звена будут:
Отсюда АФЧХ:
Передаточная функция:
В качестве примера звена можно назвать длинную электрическую линию без потерь, механический транспортер и т.д. По существу это звено относится к нелинейным. Однако при расчетах САУ с такими звеньями можно применять методы теории линейных систем. Поэтому часто элементы, закон движения которых мало изучен или трудно представим в аналитической форме, после некоторой идеализации представляются в виде звеньев запаздывания.
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 617; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.101.241 (0.01 с.) |


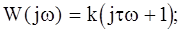





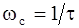 . Логарифмические частотные характеристики форсирующего звена приведены на рис. 2.16
. Логарифмические частотные характеристики форсирующего звена приведены на рис. 2.16

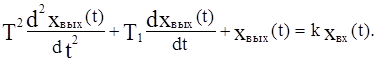
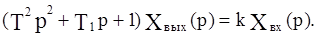



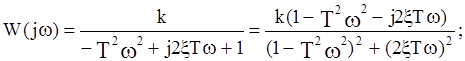








 (
(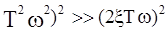 и в подкоренном выражении можно оставить лишь
и в подкоренном выражении можно оставить лишь 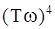 , пренебрегая остальными членами. Высокочастотная асимптота G(w)вч описывается формулой:
, пренебрегая остальными членами. Высокочастотная асимптота G(w)вч описывается формулой: , как показано на рис.2.17.
, как показано на рис.2.17. G(w) Точная ЛАЧХ
G(w) Точная ЛАЧХ lg 1/T
lg 1/T
 несколько отличается от асимптотической
несколько отличается от асимптотической  . Максимальная ошибка - в районе около сопрягающей частоты. Для упрощенных расчетов можно считать, что наибольшая ошибка будет при
. Максимальная ошибка - в районе около сопрягающей частоты. Для упрощенных расчетов можно считать, что наибольшая ошибка будет при 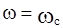 :
: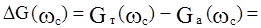

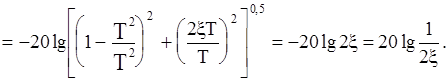
 точная ЛАЧХ идет ниже асимптотической при
точная ЛАЧХ идет ниже асимптотической при 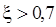 и выше - при
и выше - при 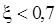 . При значениях
. При значениях  ошибка становится существенной (более трех децибел) и ее необходимо учитывать, используя приведенную выше формулу либо поправочные кривые из справочной литературы.
ошибка становится существенной (более трех децибел) и ее необходимо учитывать, используя приведенную выше формулу либо поправочные кривые из справочной литературы.
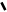






 k
k







 0 t
0 t