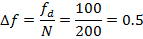Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Спектри зашумлених сталих сигналівСодержание книги
Поиск на нашем сайте
Звіт до практичної роботи №4 по дисципліні системи обробки сигналів та зображень (СОСЗ) на тему: «Спектральний аналіз сигналів»
Перевірив: Виконали: Ігнатенко В.М. студенти групи ІК-92 Кобилинський Б.А. Чернявський Д.Ю.
Київ 2011 Зміст 1. Теоретичні відомості. 2. Зміст та програма виконання роботи. 3. Результати виконання роботи. 3.1. Спектри сталих сигналів. 3.2. Спектри зашумлених сталих сигналів. 3.3. Спектри періодичних сигналів. 3.4. Зашумлені періодичні сигнали. 3.5. Методика визначення аналітичного виразу по його спектру. 3.6. Спектри неперіодичних сигналів. 3.6.1. Незашумлений експоненціальний сигнал. 3.6.2. Зашумлений експоненціальний сигнал. 3.7. Модульовані сигнали. 3.7.1. Незашумлені модульовані сигнали 3.7.2. Зашумлені модульовані сигнали 3.8. Фільтрація зашумлених сигналів 3.8.1. Фільтрація зашумленого сталого сигналу 3.8.2. Фільтрація зашумленого гармонічного сигналу 3.8.3. Фільтрація зашумленого періодичного сигналу 3.8.4. Фільтрація зашумленого експоненціального сигналу 3.8.5. Фільтрація зашумленого модульованого сигналу 3.8.6. Фільтрація зашумленого спектру в ПП Spectr 4. Загальні висновки
Практична робота №4 Спектральний аналіз сигналів Мета: Вивчення властивостей спектрів різних дискретних сигналів. Набуття навичок проведення спектрального аналізу сигналів; спектральний аналіз сигналів різного характеру.
1. Теоретичні відомості: Спектромсигналу називаються гармонічні (синусоїдальні) складові, якими подається цей сигнал. Спектр дискретизованого сигналу діє на амплітудний і фазовий спектри і є комплексною величиною. Амплітудний спектр – модуль комплексної величини. Фазовий спектр – фаза комплексної величини.
Спектр дискретизованого сигналу має такі властивості: 1) Спектр подається з певним кроком (періодом, інтервалом) на фіксованому інтервалі частоти, який дорівнює частоті дискретизації сигналу. 2) Спектр дискретизованого сигналу є нескінченно періодичним, але для обмеженого сигналу у часі подається обмеженим. 3) Значення амплітудного і фазового спектру характеризується такими параметрами: - Амплітуда - Частота - Фаза - Характер сигналу Спектральним аналізом називається побудова спектрів сигналів (амплітудних і фазових комплектуючих) і виявлення характерних властивостей спектру з метою встановлення характеру сигналу, його складових і виділення корисного сигналу і перешкоди. Алгоритм аналітичного відновлення спектру: 1) Фіксація параметрів спектру заданого сигналу 2) Логічний висновок відносно характеру сигналу Алгоритм фільтрації: 1) Виконання часового та спектрального аналізу з визначенням параметрів спектру, 2) Визначення задачі фільтрації і її параметрів на основі аналізу сигналу. 3) Формування корегую чого спектру, який задається на тому ж частотному інтервалі з тим же кроком і N, як і основний спектр. 4) Перемноження спектру сигналу на корегуючий спектр. В результаті отримується скорегований спектр. 5) Відтворення сигналу у вигляді масиву значень на основі оберненого перетворення Фур’є. 2. Зміст та програма виконання роботи: 1. Аналіз властивостей спектрів дискретних сигналів на основі заданого набору тестових сигналів. 2. Отримання аналітичних залежностей, що пов’язують значення спектру з параметрами часового сигналу. Ознайомлення та оволодіння методикою фільтрації сигналів.
Результати виконання роботи Спектри сталих сигналів Завантажуємо файл 1.xy y1(x)=1 Амплітуда = 1 Інтервал визначення - 0<x<2 Кількість дискрет N=200 Період дискретизації D=0.01 (с) Частота дискретизації f(D)=100 Гц
Обираємо ДПФ та отримуємо графік спектру. Зберігаємо 1.spk 1) Амплітудний спектр A=200 fd = 100 f=0 Td=0.01 c Спектр нескінчено-періодичний 2) Фазовий спектр рівний нулю. Спектр, заданий на інтервалі fd і подається з кроком df = fd/N. Оскільки останнє значення fN-1 = df(N-1)=0.5*199=99,5 (Гц), то частота 100 (Гц) не присутня в масиві даних і 1й повтор не присутній в спектрі. Амплітуда спектру розраховується так: Аспектр = Асигнал * N В даному сигналі Аспектр= 1*200 = 200
Висновок: Амплітудний спектр сталого сигналу має складову на нульовій частоті.
Амплітудний спектр
Амплітудний спектр гармонічного сигналу має дві основних складові: 1. додатні області частот з частотою гармонічного сигналу. 2. від'ємні області на частоті – основна частота сигналу. Амплітуда цих складових Фазовий спектр
Має дві основні складові на +f та –f, а знак фази визначається знаком синусоїди. Зміна знака при сигналі призводить до зміни фази на додатних і від’ємних частотах.
Теоретично в сигналі присутні дві складові. Висновки: хоча в сигналі немає складових на f=99, в спектрі присутні значення на цій частоті, які є повтором складової спектру на від’ємній частині.
Екпоненціальний сигнал y(x)=2.4exp(-1.7x); експоненціальний сигнал; Інтервал визначення: xє[0; 2]; Кількість дискрет = 200; Період дискретизації = 0.01 с.; Частота дискретизації = 100 Гц.
Спектр:
Висновок: Спектр нескінченно-періодичний з періодом f d - гармонічні складові присутні на всіх частотах з кроком df=fa/N. Обрабка спектру є складною і вимагає відповідних засобів. Модульовані сигнали Додаток до звіту до практичної роботи №4 по дисципліні системи обробки сигналів та зображень (СОСЗ) на тему: «Спектральний аналіз сигналів»
Перевірив: Виконали: Ігнатенко В.М. студенти групи ІК-92 Кобилинський Б.А. Чернявський Д.Ю.
Київ 2011 Звіт до практичної роботи №4 по дисципліні системи обробки сигналів та зображень (СОСЗ) на тему: «Спектральний аналіз сигналів»
Перевірив: Виконали: Ігнатенко В.М. студенти групи ІК-92 Кобилинський Б.А. Чернявський Д.Ю.
Київ 2011 Зміст 1. Теоретичні відомості. 2. Зміст та програма виконання роботи. 3. Результати виконання роботи. 3.1. Спектри сталих сигналів. 3.2. Спектри зашумлених сталих сигналів. 3.3. Спектри періодичних сигналів. 3.4. Зашумлені періодичні сигнали. 3.5. Методика визначення аналітичного виразу по його спектру. 3.6. Спектри неперіодичних сигналів. 3.6.1. Незашумлений експоненціальний сигнал. 3.6.2. Зашумлений експоненціальний сигнал. 3.7. Модульовані сигнали. 3.7.1. Незашумлені модульовані сигнали 3.7.2. Зашумлені модульовані сигнали 3.8. Фільтрація зашумлених сигналів 3.8.1. Фільтрація зашумленого сталого сигналу 3.8.2. Фільтрація зашумленого гармонічного сигналу 3.8.3. Фільтрація зашумленого періодичного сигналу 3.8.4. Фільтрація зашумленого експоненціального сигналу 3.8.5. Фільтрація зашумленого модульованого сигналу 3.8.6. Фільтрація зашумленого спектру в ПП Spectr 4. Загальні висновки
Практична робота №4 Спектральний аналіз сигналів Мета: Вивчення властивостей спектрів різних дискретних сигналів. Набуття навичок проведення спектрального аналізу сигналів; спектральний аналіз сигналів різного характеру.
1. Теоретичні відомості: Спектромсигналу називаються гармонічні (синусоїдальні) складові, якими подається цей сигнал. Спектр дискретизованого сигналу діє на амплітудний і фазовий спектри і є комплексною величиною. Амплітудний спектр – модуль комплексної величини. Фазовий спектр – фаза комплексної величини.
Спектр дискретизованого сигналу має такі властивості: 1) Спектр подається з певним кроком (періодом, інтервалом) на фіксованому інтервалі частоти, який дорівнює частоті дискретизації сигналу. 2) Спектр дискретизованого сигналу є нескінченно періодичним, але для обмеженого сигналу у часі подається обмеженим. 3) Значення амплітудного і фазового спектру характеризується такими параметрами: - Амплітуда - Частота - Фаза - Характер сигналу Спектральним аналізом називається побудова спектрів сигналів (амплітудних і фазових комплектуючих) і виявлення характерних властивостей спектру з метою встановлення характеру сигналу, його складових і виділення корисного сигналу і перешкоди. Алгоритм аналітичного відновлення спектру: 1) Фіксація параметрів спектру заданого сигналу 2) Логічний висновок відносно характеру сигналу Алгоритм фільтрації: 1) Виконання часового та спектрального аналізу з визначенням параметрів спектру, 2) Визначення задачі фільтрації і її параметрів на основі аналізу сигналу. 3) Формування корегую чого спектру, який задається на тому ж частотному інтервалі з тим же кроком і N, як і основний спектр. 4) Перемноження спектру сигналу на корегуючий спектр. В результаті отримується скорегований спектр. 5) Відтворення сигналу у вигляді масиву значень на основі оберненого перетворення Фур’є. 2. Зміст та програма виконання роботи: 1. Аналіз властивостей спектрів дискретних сигналів на основі заданого набору тестових сигналів. 2. Отримання аналітичних залежностей, що пов’язують значення спектру з параметрами часового сигналу. Ознайомлення та оволодіння методикою фільтрації сигналів.
Результати виконання роботи Спектри сталих сигналів Завантажуємо файл 1.xy y1(x)=1 Амплітуда = 1 Інтервал визначення - 0<x<2 Кількість дискрет N=200 Період дискретизації D=0.01 (с) Частота дискретизації f(D)=100 Гц
Обираємо ДПФ та отримуємо графік спектру. Зберігаємо 1.spk 1) Амплітудний спектр A=200 fd = 100 f=0 Td=0.01 c Спектр нескінчено-періодичний 2) Фазовий спектр рівний нулю. Спектр, заданий на інтервалі fd і подається з кроком df = fd/N. Оскільки останнє значення fN-1 = df(N-1)=0.5*199=99,5 (Гц), то частота 100 (Гц) не присутня в масиві даних і 1й повтор не присутній в спектрі. Амплітуда спектру розраховується так: Аспектр = Асигнал * N В даному сигналі Аспектр= 1*200 = 200
Висновок: Амплітудний спектр сталого сигналу має складову на нульовій частоті.
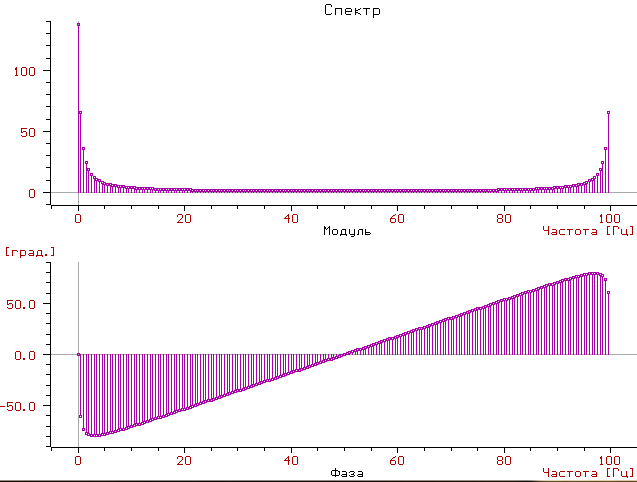
Спектри зашумлених сталих сигналів y2(x)= y2(x)+n(x); сталий сигнал з зашумленням; Рівень перешкоди: n(x)є[-0.1; 0.1]; Інтервал визначення: xє[0; 2]; Кількість дискрет = 200; Період дискретизації = 0.01с.; Частота дискретизації = 100 Гц.
Отримуємо спектр:
Висновок: На частоті f=0 маємо складову з амплітудою А = 200,8075 А також бачимо, що присутні складові на всіх частотах через наявність випадкової перешкоди в сигналі.
|
||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 318; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.211.58 (0.01 с.) |



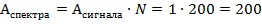 . Ця складова постійно повторюється з частотою дискретизації. Фазовий спектр є нульовим на всіх частотах.
. Ця складова постійно повторюється з частотою дискретизації. Фазовий спектр є нульовим на всіх частотах.



 . Присутні нескінчені повторення з частотою дискретизації. В таблиці, яка задає спектр на інтервалі з частотою дискретизації присутні повторення складової сигналу з від'ємною частиною.
. Присутні нескінчені повторення з частотою дискретизації. В таблиці, яка задає спектр на інтервалі з частотою дискретизації присутні повторення складової сигналу з від'ємною частиною.