
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Представление чисел в микропроцессорахСодержание книги
Поиск на нашем сайте
В зависимости от специфики применения МП числа в них могут быть представлены в разнообразных форматах. Рассмотрим представление чисел на примере восьмиразрядных процессоров. В простейших применениях управляющих МП систем широко используется способ представления целых чисел без знака в двоичном коде (рисунок 1.5,а). Диапазон представления чисел невелик и составляет от 0 до В МП системах, ориентированных на обработку данных, в которых, кроме логических операций, выполняются также операции сложения и вычитания, используется представление чисел со знаком (рисунок 1.5,б). При этом способе старший бит В МП системах, требующих выполнения операций над числами по правилам десятичной арифметики, используется десятичный двоично-кодированный формат (двоично-десятичные числа) (рисунок 1.5,в), в котором каждый байт условно разбивается на две тетрады, в каждой из которых кодируется десятичное число.
Рисунок 1.5. Форматы представления однобайтных чисел В случаях, когда МП система требует расширенного диапазона представления чисел, применяются многобайтные коды. На рисунке 1.6,а показан пример размещения в памяти МП системы 32-битного двоичного целого числа со знаком. Обработка таких многобайтных чисел, расположенных в смежных ячейках, осуществляется в МП побайтно, начиная с младшего байта, путем вызова соответствующей подпрограммы обработки и трехкратной модификации (инкрементирования) указателя стека. Если в МП системе необходимо выполнить обработку десятичных чисел со знаком, то такие многобайтные числа представляются в десятичном дополнительном коде. При этом старшая тетрада старшего байта числа используется для кодирования знака числа, а остальные тетрады содержат двоичные коды десятичных цифр (рисунок 1.6,б). Положительное число в знаковой тетраде кодируется четырьмя нулями, а для представления знака «минус» используется код 1001 (девятка). Для представления дробных чисел в МП может использоваться формат с плавающей точкой. Как правило, при этом два или три младших байта отводятся для представления мантиссы, а старший байт – для представления порядка числа и его знака. При этом бит Порядок p представляется обычно смещенным кодом Мантисса m представляется либо прямым, либо дополнительным кодом и должна быть нормализованной, т.е. иметь значащую старшую цифру (находиться по модулю в диапазоне от Число с плавающей точкой определяется как
что позволяет перекрывать диапазон модулей от Использование в МП системах многобайтных чисел приводит к резкому снижению производительности. Чем в большей степени формат обрабатываемых чисел (а на него нет никаких ограничений) превышает собственный формат МП (разрядность шины данных), тем значительнее снижается быстродействие обработки данных в МП системе.
Рисунок 1.6. Форматы представления многобайтных чисел
|
||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 253; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.130.96 (0.008 с.) |

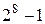 .
. отводится для знака числа (S =1 – число отрицательное, S =0 – число положительное). Положительные числа представляются модулем, а отрицательные – дополнительным кодом. Числа в этом случае могут находиться в диапазоне от
отводится для знака числа (S =1 – число отрицательное, S =0 – число положительное). Положительные числа представляются модулем, а отрицательные – дополнительным кодом. Числа в этом случае могут находиться в диапазоне от  до
до 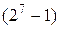 . Аналогично представляются числа двойной длины (двухбайтовые числа). Знаковый разряд располагается при этом в бите
. Аналогично представляются числа двойной длины (двухбайтовые числа). Знаковый разряд располагается при этом в бите  .
.
 определяет знак порядка:
определяет знак порядка: 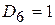 при отрицательном порядке и
при отрицательном порядке и  при положительном.
при положительном. со смещением 64 и занимает биты
со смещением 64 и занимает биты  . Значение порядка лежит в пределах
. Значение порядка лежит в пределах  , что соответствует
, что соответствует  . Бит
. Бит  в старшем байте задает знак числа: 0 соответствует плюсу, 1 – минусу (рисунок 1.6, в).
в старшем байте задает знак числа: 0 соответствует плюсу, 1 – минусу (рисунок 1.6, в). до 1). Если в процессе вычислений мантисса денормализуется, число подвергается процедуре нормализации: сдвигу мантиссы влево (или вправо) с одновременным уменьшением (или увеличением) порядка.
до 1). Если в процессе вычислений мантисса денормализуется, число подвергается процедуре нормализации: сдвигу мантиссы влево (или вправо) с одновременным уменьшением (или увеличением) порядка. ,
, до
до  .
.



