
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Таким образом, любое операционное устройство можно представить в виде композиции операционного и управляющего автоматов.Содержание книги
Поиск на нашем сайте
Операционный автомат реализует операции над словами информации и является исполнительной частью устройства, работу которого организует управляющий автомат, генерирующий необходимые последовательности управляющих сигналов. Данный подход позволяет разработать эффективные процедуры синтеза операционного и управляющего автоматов, формализовать эти процедуры и, в ряде случаев, автоматизировать процесс синтеза цифровых устройств. Технология синтеза операционных автоматов Исходные данные и основные этапы процесса разработки операционного автомата
Исходными данными для разработки структуры операционного автомата являются: описание входных и выходных слов, т. е. множеств Процесс разработки операционного автомата следует начинать с: определения форматов входных и выходных слов; разработки алгоритмов выполнения операций в терминах слов и стандартных операций над словами (сложение, копирование, инверсия, сдвиг и т. п.). Разработанные алгоритмы удобно представлять в виде блок-схем. Далее необходимо разработать структуру операционного автомата на основе операционных и логических элементов. То есть определить набор элементов, входящих в структуру, и установить связи между ними. Структура реализуется, исходя из разработанных на предыдущем этапе алгоритмов таким образом, чтобы обеспечить реализацию всех операций, указанных в операторных блоках (блоках типа процесс) блок-схемы алгоритма. Поскольку все действия в структуре операционного автомата выполняются под управлением микроопераций, то, при разработке указанного автомата, следует определить полный список микроопераций, наличие которых обеспечит выполнение в разработанной структуре всех преобразований слов, предусмотренных алгоритмами. Формирование последовательности микроопераций в управляющем автомате осуществляется с учетом значений логических условий, которые формируются в операционном автомате. Поэтому при разработке операционного автомата следует сформировать список логических условий, определяемых содержимым всех условных блоков (блоков типа решение) блок-схемы алгоритма. При необходимости, следует предусмотреть в структуре операционного автомата специальные элементы для формирования логических условий. Процесс разработки операционного автомата можно условно представить состоящим из пяти этапов: 1) определение форматов входных и выходных данных (слов); 2) разработка блок-схем алгоритмов выполняемых операций; 3) разработка структуры операционного автомата (определение элементов и организация связей между ними); 4) определение множества { y } микроопераций, выполняемых в операционном автомате; 5) определение множества { x } логических условий, формируемых в операционном автомате. Пример синтеза операционного автомата, реализующего арифметическую операцию деления 1.2.3.1 Этап определения форматов данных В арифметической операции деления участвуют два операнда – делимое Операционное устройство должно формировать следующие признаки результата: Алгоритм операции деления разрабатывается для 16-разрядных двоичных чисел в формате с фиксированной запятой в прямом двоичном коде. Знак числа сохраняется в его старшем (нулевом) бите.
В операциях участвуют переменные: 1.2.3.2 Этап разработка алгоритма операции (на примере операции деления) При выполнении деления чисел, представленных в прямых двоичных кодах, удобнее делить их модули, поскольку знак результата не зависит от соотношения модулей делимого и делителя: Поскольку деление чисел, представленных в формате с фиксированной запятой, невозможно выполнить, если модуль делимого больше либо равен модулю делителя, то следует проверить соотношение операндов путем вычитания делителя из делимого: если разность окажется положительной, то можно формировать признак переполнения Для чисел в формате с фиксированной запятой существует два алгоритма деления – без восстановления остатка и с восстановлением остатка. Сравнительный анализ алгоритмов показывает, что деление без восстановления остатка эффективнее, поскольку не требует выполнения дополнительных действий, связанных с восстановлением остатка в том случае, если в результате вычитания получилось отрицательное число. Блок-схема алгоритма деления чисел без восстановления остатка представлена на рисунке 5.
Рисунок 5 – Блок-схема алгоритма деления двоичных чисел без восстановления остатка Рассмотренный алгоритм предусматривает формирование знака результата в соответствии с приведенной выше формулой и временное сохранение его в переменной На первом этапе, выполняется пробное вычитание делителя из делимого (блок 5). Поскольку знаки операндов положительные, то появление единицы в знаковом бите В процессе определения цифр частного, роль очередного остатка играет переменная В зависимости от знака остатка После вычитания или сложения, производится сдвиг частного На последнем этапе, вычисленное значение частного копируется из переменной На этом алгоритм деления числа
|
||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 360; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.214.226 (0.007 с.) |

 и
и  ; список подмножества операций из множества
; список подмножества операций из множества 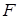 , которые должны выполняться над словами.
, которые должны выполняться над словами.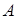 и делитель
и делитель 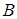 , а результатом операции является частное
, а результатом операции является частное  .
.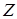 (zero) – признак нулевого результата;
(zero) – признак нулевого результата; 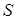 (sign) – признак отрицательного результата;
(sign) – признак отрицательного результата; 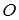 (overflow) – признак переполнения.
(overflow) – признак переполнения. – первый операнд (делимое);
– первый операнд (делимое);  – второй операнд (делитель);
– второй операнд (делитель);  – результат операции (частное) (в процессе выполнения алгоритма, используется для хранения остатка);
– результат операции (частное) (в процессе выполнения алгоритма, используется для хранения остатка);  – переменная, в которой в процессе деления накапливаются цифры частного. Биты
– переменная, в которой в процессе деления накапливаются цифры частного. Биты 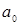 ,
, 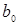 и
и  являются знаковыми.
являются знаковыми. .
. и завершать операцию; если разность окажется отрицательной, то модуль частного меньше единицы, то есть переполнение отсутствует и деление возможно.
и завершать операцию; если разность окажется отрицательной, то модуль частного меньше единицы, то есть переполнение отсутствует и деление возможно.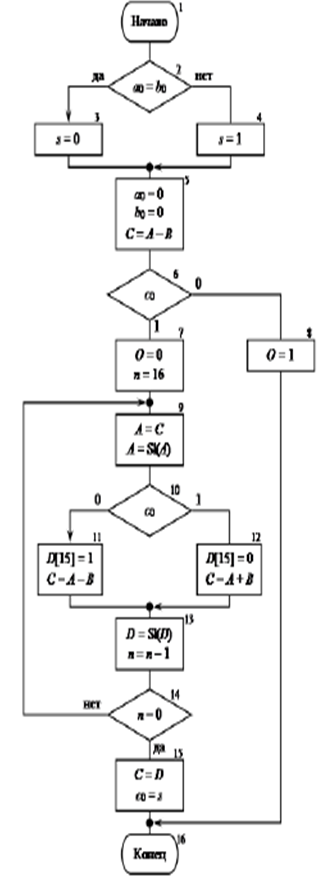
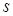 (блоки 2 - 4). После этого знаки операндов обнуляются (блок 5) и выполняется деление модулей чисел
(блоки 2 - 4). После этого знаки операндов обнуляются (блок 5) и выполняется деление модулей чисел 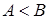 и можно продолжать деление. Если же
и можно продолжать деление. Если же 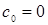 , то деление невозможно, формируется признак переполнения (блок 8) и выполнение алгоритма завершается (блок 16).
, то деление невозможно, формируется признак переполнения (блок 8) и выполнение алгоритма завершается (блок 16).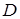 и принимается решение о характере действия на следующем шаге: вычесть делитель из сдвинутого остатка или прибавить к нему (блоки 10 – 12).
и принимается решение о характере действия на следующем шаге: вычесть делитель из сдвинутого остатка или прибавить к нему (блоки 10 – 12). цифр частного (блок 13) и проверяется условие выхода из цикла – получение шестнадцати цифр частного, включая и самую первую цифру – нуль целых (блок 14).
цифр частного (блок 13) и проверяется условие выхода из цикла – получение шестнадцати цифр частного, включая и самую первую цифру – нуль целых (блок 14).


