
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Арифметические действия над непрерывными функциями ⇐ ПредыдущаяСтр 2 из 2
Теорема. Если функции y = f (x) и g = g(x) непрерывны в точке x 0, то и функции f (x)±g(x); f (x)×g(x); Доказательство 1. Доказательство этой теоремы вытекает из определения непрерывности функции в точке и свойств пределов функций, имеющих конечные пределы. 2. Так как функции f (x) и g(x) непрерывны в точке х 0 по условию теоремы, то на основании определения №1 непрерывности функции в точке можно написать: 3. Согласно теоремам о пределах алгебраической суммы, произведения и частного двух функций, имеющих конечные пределы в точке х 0, будут существовать пределы таких функций в точке x 0: f (x) ± g(x); f (x) × g(x); а) б) в) г) 4. Но величины: f (x 0) ± g(x 0); f (x 0) × g(x 0); ч.т.д. Пример №1. Доказать, что функция y = x непрерывна в любой точке числовой прямой. Доказательство Так как приращение функции равно приращению аргумента в любой точке числовой прямой, то есть D y =D x, то ч.т.д. Пример №2. Функция такого вида y = a 0 x n + a 1 x n-1 + … + a n-1 x + a n является непрерывной в любой точке числовой прямой. Доказательство следует из теоремы и примера №1. Пример №3. Дробно - рациональная функция Доказательство следует из теоремы и примера №2.
Односторонняя непрерывность
Наряду с понятием предела функции в точке рассматривали также понятие односторонних пределов в точке (правого и левого). Поскольку определение непрерывности функции в точке даётся через понятие предела, то можно дать определение односторонней непрерывности функции в точке. Определение №1. Функция y = f (x) непрерывна справа в точке x 0, если: 1) y =f(x) определена в некоторой правосторонней d-окрестности точки x 0; 2) Существует предел функции в точке x 0 справа, т.е. 3) И этот предел равен значению функции в точке x 0, т.е. Определение №2 (на "языке e-d"). Функция y = f (x) непрерывна в точке x 0 справа, если ("e>) ($d>) (" x: x 0 £ x < x 0 + d):
Определение №3 (на "языке окрестностей"). Функция y = f (x) непрерывна в точке x 0 справа, если: ("U(f (x 0),e)) ($U(x 0 + 0,d)) (" x ÎU(x 0 + 0,d)): f (U(x 0 + 0,d)) Í U(f (x 0),e). Определение №4 (на “языке последовательности”). Функция y = f (x) непрерывна в точке x 0 справа, если: 1) 2) " { x n}® x 0, n ® ¥, x n ³ x 0 Замечание. Аналогично определяется непрерывность функции в точке x 0 слева. Определение №5. (на “языке приращений”) Функция y = f (x) непрерывна в точке х 0 справа тогда и только тогда, когда Теорема. Функция y = f (x) непрерывна в точке x 0 тогда и только тогда, когда она непрерывна слева и справа в этой точке. Доказательство необходимости 1. Пусть функция y = f (x) непрерывна в точке х 0. Требуется доказать, что функция непрерывна в точке x 0 слева и справа и 2. Так как y = f (x) непрерывна в точке х 0, то 3. На основании определения непрерывности функции в точке на "языке e-d" можно записать: ("e>)($d>)(" х: ÷ х – х 0÷<d): ÷ f (x) – f (x 0)÷<e. 4. Из неравенства ÷ х – х 0÷<d следует два неравенства: а) х 0 – d < x £ x 0 ; б) x 0 £ x < х 0 + d. 5. Они позволяют сделать вывод: 1) ("e>)($d>)(" х: х 0 –d < x £ x 0): ÷ f (x) – f (x 0)÷<e Û 2) ("e>)($d>)(" х: x 0 £ x < х 0 + d): ÷ f (x) – f (x 0)÷<e Û Следовательно, Доказательство достаточности 1. Пусть функция y = f (x) непрерывна в точке х 0 слева и справа, т.е. существуют пределы 2. На основании определения предела функции в точке слева и справа можно записать: 1) ("e>)($d>)(" х: х 0 – d < x £ x 0): ÷ f (x) – f (x 0)÷<e; 2) ("e>)($d>)(" х: x 0 £ x < х 0 + d): ÷ f (x) – f (x 0)÷<e. 3. Неравенства х 0 – d < x £ x 0 и x 0 £ x < х 0 + d можно представить в виде равносильности х 0 – d < x < х 0 + d Û x ÎU(х 0, d).
4. Следовательно, ("e>)($d>)(" х ÎU (х 0, d)): 5. Таким образом, функция y = f (x) непрерывна в точке х 0. ч.т.д. Следствие. Функция y = f(x) непрерывна в точке 1) Функция определена в некоторой окрестности точки 2) 3) 4) Пример. Показать, что функция точке x 0 =2. Решение Известно, что функция Следовательно, функция 1. Следовательно, 2. Определим значение функции в точке 3. Функция
4. Так как Модуль Тема №4
|
||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 1461; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.66.151 (0.012 с.) |
 при g(x)¹0; C× f (x), где C – const, также непрерывны в точке x 0.
при g(x)¹0; C× f (x), где C – const, также непрерывны в точке x 0. и
и 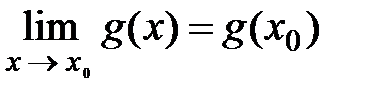 .
. ;
; ;
; ;
; .
. , g(x 0) ¹ 0; C × f (x 0) являются значениями соответствующих функций в точке х 0. Следовательно, согласно определения №1 непрерывности функции в точке функции f (x) ± g(x); f (x) × g(x);
, g(x 0) ¹ 0; C × f (x 0) являются значениями соответствующих функций в точке х 0. Следовательно, согласно определения №1 непрерывности функции в точке функции f (x) ± g(x); f (x) × g(x);  , а значит, рассматриваемая функция непрерывна в любой точке числовой прямой.
, а значит, рассматриваемая функция непрерывна в любой точке числовой прямой. является непрерывной на всей числовой прямой, исключая нули знаменателя.
является непрерывной на всей числовой прямой, исключая нули знаменателя. ;
; .
. .
.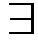 U(x 0 + 0,d) Í Df;
U(x 0 + 0,d) Í Df;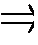 { f (x n)} ® f (x 0) при n ® ¥.
{ f (x n)} ® f (x 0) при n ® ¥. , т.е. бесконечно малому неотрицательному приращению аргумента соответствует бесконечно малое приращение функции: D x ® 0, D x ³ 0 Þ D f (x 0)® 0.
, т.е. бесконечно малому неотрицательному приращению аргумента соответствует бесконечно малое приращение функции: D x ® 0, D x ³ 0 Þ D f (x 0)® 0. .
. согласно определения №1 непрерывности функции в точке х 0.
согласно определения №1 непрерывности функции в точке х 0. ;
; .
. , т.е. функция y = f (x) будучи непрерывной в точке х 0, непрерывна в точке х 0 слева и справа.
, т.е. функция y = f (x) будучи непрерывной в точке х 0, непрерывна в точке х 0 слева и справа. . Требуется доказать, что она непрерывна в самой точке х 0, т.е.
. Требуется доказать, что она непрерывна в самой точке х 0, т.е. 
 .
. тогда и только тогда, когда:
тогда и только тогда, когда: ;
; ;
; .
. непрерывна в
непрерывна в непрерывна в точке x 0ÎR\{0}. Значит, функция
непрерывна в точке x 0ÎR\{0}. Значит, функция  непрерывна в каждой точке x 0ÎR\{1}.
непрерывна в каждой точке x 0ÎR\{1}.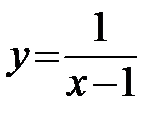 будет непрерывна в точке x 0 =2.
будет непрерывна в точке x 0 =2. .
. :
:  .
.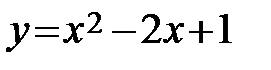 непрерывна в каждой точке x 0ÎR. Следовательно, она непрерывна и в точке x 0 =2, будет существовать
непрерывна в каждой точке x 0ÎR. Следовательно, она непрерывна и в точке x 0 =2, будет существовать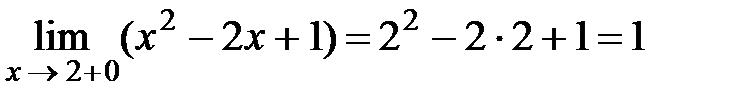 .
.
 , x 0 =2, то заданная функция f (x) непрерывна в точке x 0 =2.
, x 0 =2, то заданная функция f (x) непрерывна в точке x 0 =2.


