
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мінімізація за допомогою діаграм Вейча (або карт Карно)Содержание книги
Поиск на нашем сайте
В переглянутому прикладі для мінімізації функції ми використали шлях алгебраїчних перетворень. Цей шлях універсальний, але кінцевий результат залежить від кваліфікації фахівця, що проводить мінімізацію. Для функцій, що мають не більше п'яти-шести аргументів, зручно проводити мінімізацію за допомогою діаграм Вейча. Попередньо потрібно представити функцію в ДДНФ формі, заповнити прямокутну таблицю, ставлячи 1 в клітинки таблиці при рівності одиниці, відповідних кон’юнкцій початкової функції, і 0 в решту клітинок таблиці. На рис. 2 подані карти Карно для функцій декількох змінних.
В заповненій таблиці обводять контурами всі одиниці, а потім записують мінімізовану функцію в вигляді суми логічних добутків, що описують ці функції. В середині контуру повинні знаходитись тільки клітинки, заповнені одиницями, число яких повинно бути цілою ступінню числа 2, а одні і ті ж клітинки можуть входити в декілька контурів. Мінімізуємо за допомогою карти Карно функцію трьох змінних
В даному випадку всі одиниці в таблиці можна охватити трьома контурами. Виписавши позначення цих контурів, отримаємо мінімізовану функцію F = X1X2 + X1X3 + X2X3.
Логічні елементи. Логічний елемент - це електронний пристрій, що реалізує одну з логічних функцій. На принциповій схемі логічний елемент відображають прямокутником, всередині якого ставиться зображення показника функції. Лінії з лівої сторони прямокутника показують входи, з правої - виходи елемента. Графічне зображення більш поширених вентилів подані у таблиці (інверсні входи і виходи позначаються кружками).
Розглянемо принципові схеми пристроїв та їх логічний синтез. Пристрій для порівняння двох однорозрядних двійкових чисел X1, Х2 і визначення моменту, коли вони будуть рівні. 1. Логічними аргументами Х1 і Х2 будуть порівнювані двійкові числа, тоді функція Y = f (Х1 Х 2) визначатиме момент, коли аргументи будуть рівні. Будь-яке однорозрядне двійкове число може набувати значення 1 або 0. Визначимо всі можливі комбінації значень двох таких чисел: 0-0; 0-1; 1-0; 1-1. Виходячи з умови роботи пристрою, функція У має дорівнювати 1 тільки для першої і четвертої комбінацій, тобто у випадку, коли значення Х1 і Х2 будуть рівні. Для другої і третьої комбінацій функція дорівнює 0. 2. На основі складеного словесного опису логічної функції Y побудуємо таблицю її істинності (таблиця 2.1.6).
Таблиця 2.1.6 – Таблиця істинності функції Y
3. Виведемо, користуючись таблицею 5.1.6, логічне рівняння в ДДНФ:
У =
Результат логічного синтезу: пристрій має виконувати операції, як задовольняють логічне рівняння:
Y =
Визначену функцію називають функцією рівнозначності. Рівняння має два знаки інверсії, два знаки множення і один знак логічної суми, отже, щоб скласти схему, потрібно відповідно мати: два логічних елементи НЕ, два логічних елементи І і один елемент АБО. Складемо принципову схему пристрою за таким планом. Візьмемо елемент І (на схемі його позначено D1) і подамо на його входи лінії, якими передаватимуться сигнали X1 і Х2, що відповідають порівнюваним розрядам двійкових чисел. На виході цього елемента утворюється логічний добуток X1* Х2. Візьмемо елемент НЕ (Б2) і, подавши на його вхід сигнал з лінії Х1 дістанемо на виході За допомогою другого елемента НЕ (DЗ) виконаємо аналогічну процедуру для сигналу з лінії Х2. Виходи з обох елементів "НЕ" під'єднаємо до входів другого елемента І (D4), на виході якого формується добуток З'єднаємо виходи обох елементів І з входами елемента АБО (D5), вихід якого і відповідає вихідному логічному рівнянню. Як наслідок, схема матиме такий вигляд (рисунок 2.1.12).
Рисунок 2.1.12 – Логічна схема для визначення рівності двох однорозрядних двійкових чисел
Тригери На відміну від комбінаційних логічних ланцюгів, тригери - це логічні пристрої з пам’яттю. Їх вхідні сигнали в загальному випадку залежать не тільки від сигналів, що прикладені до входів в даний момент часу, але й від сигналів, що діяли на них раніше. В залежності від властивостей, кількості і призначення, входів, тригери поділяються на декілька видів [6, 9]. Розрізняють тактовані та нетактовані тригери. Зміна стану нетактованого (асинхронного) тригера відбувається одразу після відповідної зміни потенціалів на його управляючих входах. В тактованому (синхронному) тригері зміна стану може відбутися тільки в момент присутності відповідного сигналу на тактовому вході. Тактування може відбуватися імпульсом (потенціалом) або фронтом (перепадом потенціалу). В першому випадку сигнали на управляючих входах впливають на стан тригера тільки при дозволяючому потенціалі на тактовому вході. В другому випадку дія управляючих сигналів проявляється тільки в момент переходу одиниця-нуль або нуль-одиниця на тактовому вході. Існують також універсальні тригери, які можуть працювати як в тактованому, так і в нетактованому режимах. Основні типи тригерів в інтегральному виконанні мають наступні назви: D-тригери, T-тригери, RS-тригери і JK-тригери.
На рис. 2.8 наведена почасова діаграма перехідних процесів в схемі при подачі на неї управляючих сигналів.
Вихідний стан тригера - нульовий, на його входи по черзі поступають спочатку сигнал S, потім, після його закінчення - сигнал R. З діаграми видно, що після закінчення вхідного сигналу тригер може зберігати свій новий стан скільки потрібно довго. Говорять, що тригер запам'ятовує вхідний сигнал.
В ТТЛ-серіях практично всі тригери будуються по схемі, наведеній на рис. 2.10., а.
Основне призначення тригерів в цифрових схемах - зберігання вироблених логічними схемами результатів. Для відсічення спотворених перехідними процесами результатів між виходом логічної схеми і входом тригера можна включити кон'юнктор типу елемента С на рис. 2.11.
D-тригер (тригер защіпка) - синхронний тригер, що має два входи: вхід даних D і вхід синхронізації. D-тригер перемикається тільки по сигналу на С-вході і при тому в стан, що вказує D-вхід. С-сигнали в цьому випадку відіграють роль команди “записати в тригер”. Одна з можливих функціональних схем однотактного D-тригера і його умовне позначення наведені на рис. 2.12.
Особливості нововведення D-тригера (прозорої защіпки) ілюструє діаграма на рис. 2.13.
В серіях мікросхем, що випускаються, є також універсальні JK-тригери, які при відповідному підключенні вхідної логіки можуть виконувати функції тригерів будь-яких інших типів. JK-тригери являють собою послідовні регенеративні бістабільні пристрої з двома інформаційними входами J і K, які на випадок вхідної комбінації J=K=1 перемикають тригер в протилежний стан подібно Т-тригеру, а при будь-яких інших комбінаціях вони функціонують як RS-тригер, в якого роль входів S і R виконують відповідні входи J і K: J≡S, K≡R
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 885; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.166.223 (0.007 с.) |





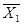 *
* 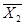 +Х1 *Х2. (2.1.1)
+Х1 *Х2. (2.1.1)
 Найпростіші нетактовані RS-тригери (рис. 2.7., а) представляють собою два ланцюги АБО-НІ, замкнуті в кільце. Такий тригер має два входи: S (встановлення) і R (скид), два виходи Q і Q.
Найпростіші нетактовані RS-тригери (рис. 2.7., а) представляють собою два ланцюги АБО-НІ, замкнуті в кільце. Такий тригер має два входи: S (встановлення) і R (скид), два виходи Q і Q.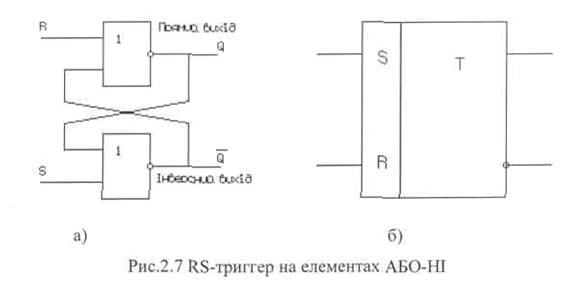
 Поки на обох управляючих входах R та S рівні сигналів не активні, в даному випадку рівні 0, тригер знаходиться в будь-якому одному з двох стійких станів. Якщо значення сигналу на виході Q дорівнює 1, то, як видно зі схеми, цей одиничний сигнал, поступаючи по колу зворотного зв'язку на вхід нижнього елементу, викликає появу на виході Q сигналу з нульовим рівнем. В свою чергу, нульовий рівень виходу Q, поступаючи на вхід верхнього елемента, підтримує Q в стані 1. В цьому випадку говорять, що тригер встановлений. В силу симетрії схеми вона буде стільки ж стійка в протилежному - нульовому стані, коли рівень на виході Q дорівнює 0 - тригер скинутий. Режим RS-тригера, коли обидва управляючих сигнали R і S неактивні, називають режимом зберігання.
Поки на обох управляючих входах R та S рівні сигналів не активні, в даному випадку рівні 0, тригер знаходиться в будь-якому одному з двох стійких станів. Якщо значення сигналу на виході Q дорівнює 1, то, як видно зі схеми, цей одиничний сигнал, поступаючи по колу зворотного зв'язку на вхід нижнього елементу, викликає появу на виході Q сигналу з нульовим рівнем. В свою чергу, нульовий рівень виходу Q, поступаючи на вхід верхнього елемента, підтримує Q в стані 1. В цьому випадку говорять, що тригер встановлений. В силу симетрії схеми вона буде стільки ж стійка в протилежному - нульовому стані, коли рівень на виході Q дорівнює 0 - тригер скинутий. Режим RS-тригера, коли обидва управляючих сигнали R і S неактивні, називають режимом зберігання.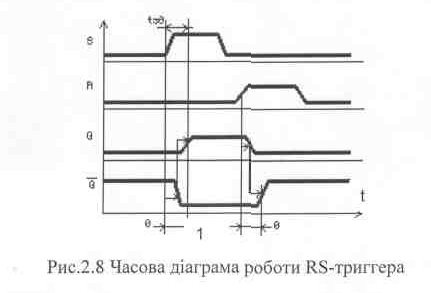
 Якщо на RS-тригер подати одночасно обидва вхідних сигнали, то на обох виходах Q і Q появляться нулі. Якщо тепер одночасно зняти одиниці з входів R і S, то обидва елемента почнуть переключатись в одиничний стан, кожен при цьому буде намагатись залишити свого партнера в нульовому стані. Який елемент отримає перемогу в цьому поєдинку, буде залежати від їх коефіцієнтів підсилення, швидкості перехідних процесів та інших факторів. Результуючий стан тригера стає невизначеним, тому комбінація R=S=1 вважається забороненою.
Якщо на RS-тригер подати одночасно обидва вхідних сигнали, то на обох виходах Q і Q появляться нулі. Якщо тепер одночасно зняти одиниці з входів R і S, то обидва елемента почнуть переключатись в одиничний стан, кожен при цьому буде намагатись залишити свого партнера в нульовому стані. Який елемент отримає перемогу в цьому поєдинку, буде залежати від їх коефіцієнтів підсилення, швидкості перехідних процесів та інших факторів. Результуючий стан тригера стає невизначеним, тому комбінація R=S=1 вважається забороненою.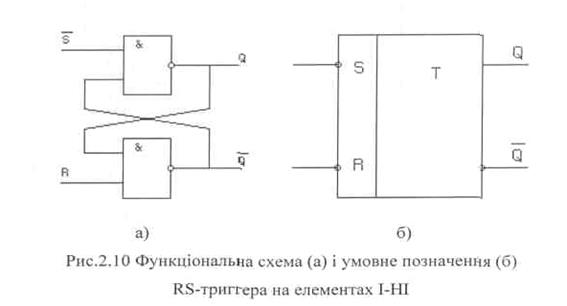


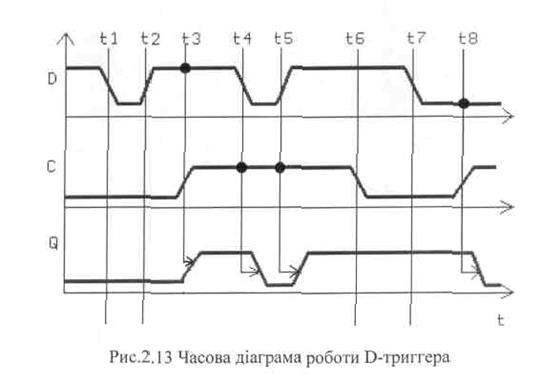
 Зміни D-входу при С=0 (моменти t1, t2, t7) ніяк не впливають на стан виходу Q: тригер закритий по входу С і знаходиться в режимі зберігання. Фронт С-сигналу (момент t3) викликає перемикання тригера в той стан, який був до цього моменту на вході D. При С=1 защіпка прозора: будь-яка зміна D-входу (моменти t4, t5 ) викликає зміну виходу Q. По зрізу синхросигналу (момент t6 ) тригер фіксує на виході той стан, який був на D-вході. Наступна зміна Q можлива тільки по фронту наступного синхроімпульса (момент t8). Якщо на С-вхід подати постійний одиничний імпульс, то властивість запам'ятовування защіпки проявлятись ніяк не буде і вона буде виконувати функції звичайного буферного підсилювача потужності в тракті передачі даних. Якщо вхід D тригера (рис.2.12) з'єднати з його інверсним виходом (D=Q), то кожен перепад на його тактовому вході буде приводити до переходу тригера в протилежний стан, частота сигналу на виході Т-тригера в два рази нижче частоти сигналу на вході, через це такий тригер можна використати як подільник частоти і двійковий лічильник.
Зміни D-входу при С=0 (моменти t1, t2, t7) ніяк не впливають на стан виходу Q: тригер закритий по входу С і знаходиться в режимі зберігання. Фронт С-сигналу (момент t3) викликає перемикання тригера в той стан, який був до цього моменту на вході D. При С=1 защіпка прозора: будь-яка зміна D-входу (моменти t4, t5 ) викликає зміну виходу Q. По зрізу синхросигналу (момент t6 ) тригер фіксує на виході той стан, який був на D-вході. Наступна зміна Q можлива тільки по фронту наступного синхроімпульса (момент t8). Якщо на С-вхід подати постійний одиничний імпульс, то властивість запам'ятовування защіпки проявлятись ніяк не буде і вона буде виконувати функції звичайного буферного підсилювача потужності в тракті передачі даних. Якщо вхід D тригера (рис.2.12) з'єднати з його інверсним виходом (D=Q), то кожен перепад на його тактовому вході буде приводити до переходу тригера в протилежний стан, частота сигналу на виході Т-тригера в два рази нижче частоти сигналу на вході, через це такий тригер можна використати як подільник частоти і двійковий лічильник.


