
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Доказательства методом площадейСтр 1 из 4Следующая ⇒
Через подобные треугольники
Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC. Введя обозначения
Что эквивалентно
Сложив, получаем
или
Доказательства методом площадей
Доказательство через равнодополняемость
1. 2. 3.
Что и требовалось доказать.
Доказательства через равносоставленность
Доказательство Евклида
Рассмотрим чертеж справа. На нём мы построили квадраты на сторонах прямоугольного треугольника и провели из вершины прямого угла С луч s перпендикулярно гипотенузе AB, он рассекает квадрат ABIK, построенный на гипотенузе, на два прямоугольника — BHJI и HAKJ соответственно. Оказывается, что площади данных прямоугольников в точности равны площадям квадратов, построенных на соответствующих катетах. Попытаемся доказать, что площадь квадрата DECA равна площади прямоугольника AHJK. Для этого воспользуемся вспомогательным наблюдением: площадь треугольника с той же высотой и основанием, что и данный прямоугольник, равна половине площади заданного прямоугольника. Это следствие определения площади треугольника как половины произведения основания на высоту. Из этого наблюдения вытекает, что площадь треугольника ACK равна площади треугольника AHK (не изображённого на рисунке), которая, в свою очередь, равна половине площади прямоугольника AHJK.
Д Рассуждение о равенстве площадей квадрата BCFG и прямоугольника BHJI совершенно аналогично. Тем самым мы доказали, что площадь квадрата, построенного на гипотенузе, слагается из площадей квадратов, построенных на катетах. Идея данного доказательства дополнительно проиллюстрирована с помощью анимации, расположенной выше. 2Свойство и признак касательной к окружности.
ОПРЕДЕЛЕНИЕ Окружностью называется геометрическое место точек, равноудаленных от одной точки, которая называется центром окружности.
Отрезок, соединяющий две точки окружности, называется хордой (на рисунке это отрезок). Хорда, проходящая через центр окружности, называется диаметром окружности.
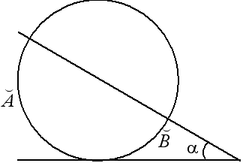
1. Касательная перпендикулярна радиусу, проведенному в точку касания. 2. Отрезки касательных, проведенных из одной точки, равны. 3. Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть:
Свойства высот треугольника Теорема Фалеса. Если стороны угла пересечены параллельными прямыми, то отрезки, отсекаемые ими на одной стороне этого угла, пропорциональны соответственным отрезкам, отсекаемым ими на другой его стороне. Обратная теорема Фалеса. Если на одной стороне угла от его вершины O отложены отрезки OA, AB, BC,... и на другой его стороне также от вершины O отложены соответственно пропорциональные им отрезки OA1, A1B1, B1C1,... (OA/OA1= AB/AB2= BC/BC2=k), то прямые AA1, BB1, CC1, - параллельны.
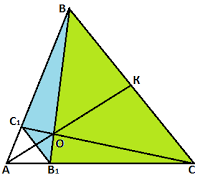
Тренировочная работа №10 задание 16. Точки В1 и С1 лежат на сторонах соответственно AC и AB треугольника ABC, причем АВ1: В1С = АС1: С1В. Прямые ВВ1 и СС1 пересекаются в точке О. а) Докажите, что прямая АО делит пополам сторону BC. б) Найдите отношение площади четырехугольника АВ1ОС1 к площади треугольника ABC, если известно, что АВ1: В1С = АС1: С1В = 1:4.
Решение: а) Так как точки В1 и С1 делят стороны треугольника в одинаковых отношениях, то по теореме обратной теореме Фалеса прямая В1С1 всегда будет параллельна BC. Отсюда следует, что четырёхугольник ВСВ1С1 – трапеция. По теореме о четырех точках трапеции середины оснований, точка пересечения диагоналей и точка пересечения боковых сторон лежат на одной прямой. Таким образом, прямая АО проходит через середины оснований трапеции ВСВ1С1. б) Треугольник АВ1С1 подобен треугольнику АВС с коэффициентом подобия 1/5, следовательно, его площадь будет составлять 1/25 площади треугольника АВС или S/25. Тогда площадь трапеции ВСВ1С1 составляет 24/25 площади треугольника АВС, то есть 24S/25. Высота треугольника ВВ1С1, проведённая к стороне В1С1, равна высоте треугольника ВВ1С, проведённой к стороне ВС. Поскольку В1С1в пять раз меньше ВС, то площадь треугольника ВВ1С1в пять раз меньше, чем площадь треугольника ВВ1С1. Обозначим площадь треугольника ВВ1С1 – х, тогда площадь треугольника ВВ1С – 5 х. Значит, х + 5х = 24S/25, 6х = 24S/25, х = 4S/25. То есть площадь треугольника ВВ1С1 равна 4S/25, площадь треугольника ВВ1С равна 20S/25. Рассмотрим треугольники ВСС1 и ВСВ1. Так как у них общее основание – ВС, и одинаковая высота, то их площади равны. В состав каждого из них входит треугольник ОВС, поэтому площади треугольников ВВ1С1 и СВ1С1 равны, пусть они равны р. Треугольники ОВ1С1 и ОВС подобны с коэффициентом подобия 1/5. Если обозначим площадь треугольника ОВ1С1 через а, то площадь треугольника ОВСравна 25 а. Так как площадь треугольника ВВ1С1 равна сумме площадей треугольников ВОС и В1ОС, получаем 4S/25 = а +р. Так как площадь треугольника ВВ1С равна сумме площадей треугольников ОВ1С1 и ВОС1, получаем 20S/25 =25 а +р. Вычитая из этого равенства предыдущее, получаем 16S/25 =24а. Отсюда а = 2S/75. Площадь четырехугольника АВ1ОС1 = S/25 +2S/75 = S/15 Ответ: 1:15.
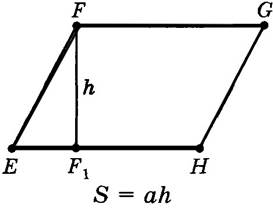
11Вывод формул площадей параллелограмма, треугольника и трапеции. Площадь треугольника, трапеции, параллелограмма · Площадь треугольника равна половине произведения основания треугольника на высоту. · Площадь трапеции равна произведению полусуммы его оснований на высоту. · Площадь параллелограмма равна произведению его основания на высоту.
Используя рисунки выше, необходимо вспомнить, как доказывается утверждение, что «Если а является основанием треугольника, h — проведенная к нему высота, S — площадь треугольника, то
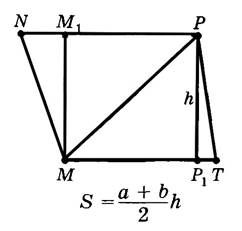
С помощью рисунка выше вспомните доказательство утверждения: «Если а и b — основания трапеции, h — ее высота, S — площадь трапеции, то
Используя данное утверждение о площади трапеции и рисунок ниже, вспомните доказательство утверждения: «Если а — основание параллелограмма, h — проведенная к нему высота, S — площадь параллелограмма, то S = ah».
Формула Герона Теорема: Если а, b с — стороны треугольника, р — полупериметр, р=(a+b+c)/2, r — радиусвписанной окружности, S — площадь треугольника, то:
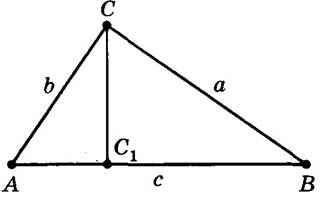
Доказательство. Пусть а, b, с — длины сторон ВС, АС, АВ треугольника ABC (рисунок).
Проведем высоту CC1 и обозначим х длину отрезка АС1. Тогда ВС1=с-х. По теореме Пифагора получаем:
Решим это уравнение и найдем х:
Тогда:
Данная формула называется формулой Герона. Герон Александрийский (I в.) — древнегреческий ученый, который работал в Александрии. Математические работы Герона являются энциклопедией античной практической математики.
Определение параллелограмма
Параллелограмм – четырехугольник, у которого противоположные стороны попарно параллельны.
Частные случаи параллелограмма: ромб, прямоугольник, квадрат. Свойства параллелограмма
1. Противоположные стороны параллелограмма попарно равны 2. Противоположные углы параллелограмма попарно равны
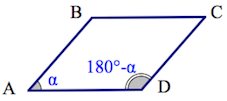
3. Сумма смежных (соседних) углов параллелограмма равна 180 градусов 4. Сумма всех углов равна 360°
6. Точка пересечения диагоналей является центром симметрии параллелограмма
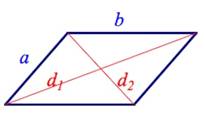
7. Диагонали параллелограмма и стороны
8. Биссектриса отсекает от параллелограмма равнобедренный треугольник
Признаки параллелограмма
Четырехугольник является параллелограммом, если выполняется хотя бы одно из следующих условий: 1. Противоположные стороны попарно равны: 2. Противоположные углы попарно равны: 3. Диагонали пересекаются и в точке пересечения делятся пополам 4. Противоположные стороны равны и параллельны: 5.
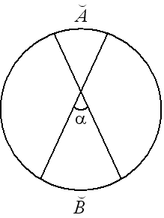
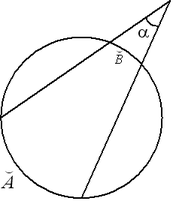
14 Углы, связанные с окружностью
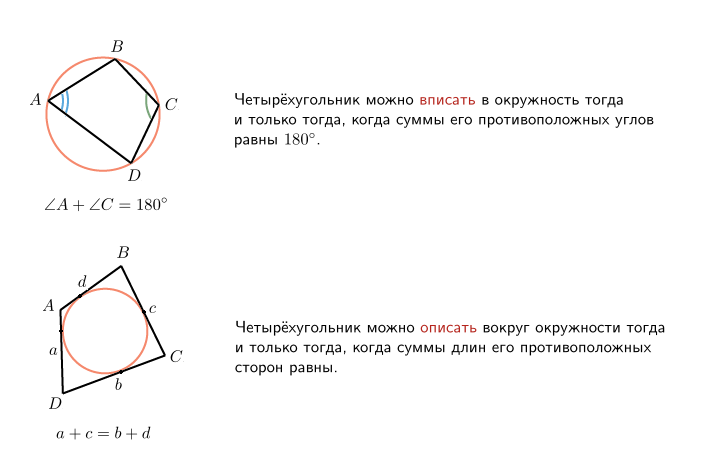
15-16 15Вписанные и 16описанные четырехугольники Вписанный четырехугольник — четырехугольник, все вершины которого лежат на одной окружности. Описанный четырехугольник — такой, что все его стороны касаются одной окружности. В этом случае окружность вписана в четырехугольник. На рисунке — вписанные и описанные четырехугольники и их свойства.
Посмотрим, как эти свойства применяются в решении задач ЕГЭ.
Сумма противоположных углов вписанного четырехугольника равна Ответ:
Пусть сторона Ответ:
Мы помним, что средняя линия трапеции равна полусумме оснований. Пусть основания трапеции равны Еще раз повторим свойства вписанного и описанного четырехугольника. Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы его противоположных углов равны Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы длин его противоположных сторон равны. Докажите эти утверждения. Это задание особенно полезно тем, кто нацелен на решение части С.
Признаки параллельности прямой и плоскости:
1) Если прямая, лежащая вне плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельна этой плоскости.
2) Если прямая и плоскость перпендикулярны одной и той же прямой, то они параллельны.
Признаки параллельности плоскостей:
1) Если две пересекающиеся прямые одной плоскости cоответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
2) Если две плоскости перпендикулярны одной и той же прямой, то они параллельны.
Признаки перпендикулярности прямой и плоскости:
1) Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.
2) Если плоскость перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.
Наклонная к плоскости. Прямая, пересекающая плоскость и не перпендикулярная ей, называется наклонной к плоскости.
Теорема о трёх перпендикулярах. Прямая, лежащая в плоскости и перпендикулярная проекции наклонной к этой плоскости, перпендикулярна и самой наклонной.
Признаки параллельности прямых в пространстве:
1) Если две прямые перпендикулярны одной и той же плоскости, то они параллельны.
2) Если в одной из пересекающихся плоскостей лежит прямая, параллельная другой плоскости, то она параллельна линии пересечения плоскостей.
Признак перпендикулярности плоскостей: если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Теорема об общем перпендикуляре к двум скрещивающимся прямым. Для любых двух скрещивающихся прямых существует единственный общий перпендикуляр.
Геометрия Перпендикулярность двух плоскостей
Определение: две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения плоскостей, пересекает их по перпендикулярным прямым.
Свойство
Если прямая, лежащая в одной из двух перпендикулярных плоскостей, перпендикулярна линии их пересечения, то она перпендикулярна и другой плоскости.
.Признак параллельности прямой и плоскости Прямая и плоскость называются параллельными, если они не имеют общих точек.Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой 1.Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой. 2.Если одна из двух параллельных прямых параллельна данной плоскости, а другая прямая имеет с плоскостью общую точку, то эта прямая лежит в данной плоскости. плоскости, то она параллельна самой плоскости. Случаи взаимного расположения прямой и плоскости: а) прямая лежит в плоскости; б) прямая и плоскость имеют только одну общую точку;в) прямая и плоскость не имеют ни одной общей точки. 2.Определение натуральной величины отрезка прямой общего положения способом прямоугольного треугольника. Натуральная величина (н.в.) отрезка АВ прямой общего положения является гипотенузой прямоугольного треугольника АВК. В этом треугольнике катет АК параллелен плоскости проекций π1 и равен горизонтальной проекции отрезка A'B'. Катет BK равен разности расстояний точек A и B от плоскости π1.
В общем случае для определения натуральной величины отрезка прямой необходимо построить гипотенузу прямоугольного треугольника, одним катетом которого является горизонтальная (фронтальная) проекция отрезка, другим катетом — отрезок, равный по величине алгебраической разности координат Z (Y) крайних точек отрезка. Из прямоугольного треугольника находят угол α — угол наклона прямой к горизонтальной плоскости проекций. Для определения угла наклона прямой к фронтальной плоскости проекций необходимо выполнить аналогичные построения на фронтальной проекции отрезка. 3.Главные линии плоскости (горизонталь, фронталь). Горизонталь плоскости Р – прямая, которая лежит в этой плоскости и параллельна горизонтальной плоскости. Горизонталь как прямая, параллельная горизонтальной плоскости, имеет фронтальную проекцию ѓ, параллельную оси х.
Фронталь плоскости Р – прямая, которая лежит в этой плоскости и параллельна фронтальной плоскости. Фронталь является прямой, параллельной фронтальной плоскости, и ее горизонтальная проекцияф параллельна оси х.
4.Взаимное положение прямых в пространстве. Определение видимости по конкурирующим точкам. Две прямые в пространстве могут иметь различное расположение: А)пересекаться (лежать в одной плоскости). Частный случай пересечения – под прямым углом;Б)могут быть параллельными (лежать в одной плоскости);В)совпадать – частный случай параллельности;Г)скрещиваться (лежать в разных плоскостях и не пересекаться). Точки, у которых проекции на П1 совпадают, называют конкурирующими по отношению к плоскости П1, а точки, у которых проекции на П2 совпадают, называют конкурирующими по отношению к плоскости П2.
Точки К и L конкурирующие по отношению к плоскости П1, так как на плоскости П1 точки К и L проецируются в одну точку: К1 = L1. Точка К выше точки L, т.к. К2 выше точки L2, потому К1 на П1 видима. Две плоскости называются параллельными, если они не имеют общих точек, т.е. если α Теорема 1. Через точку, не лежащую в плоскости, можно провести только одну плоскость, параллельную данной плоскости. Доказательство. Пусть даны плоскость а и точка А, А Пусть это не так, т.е. плоскости пересекаются по прямой с. Тогда по меньшей мере одна из прямых а или b не параллельна прямой с. Для определенности положим, что а Следовательно, a1 Это противоречит тому, что а, || а. Поэтому α Теорема 2. Если пересечь две параллельные плоскости третьей плоскостью, то прямые их пересечения будут параллельными, т.е α
Итак, две плоскости в пространстве могут взаимно располагаться в двух вариантах: · плоскости пересекаются по прямой; · плоскости параллельны.
Теорема 3. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны. Теорема 4. Отрезки параллельных прямых, ограниченных параллельными плоскостями, равны, между собой.
Через подобные треугольники
Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC. Введя обозначения
Что эквивалентно
Сложив, получаем
или
Доказательства методом площадей
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 1739; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.251.68 (0.161 с.) |
 получаем
получаем







 дея доказательства Евклида состоит в следующем: попробуем доказать, что половина площади квадрата, построенного на гипотенузе, равна сумме половин площадей квадратов, построенных на катетах, а тогда и площади большого и двух малых квадратов равны.
дея доказательства Евклида состоит в следующем: попробуем доказать, что половина площади квадрата, построенного на гипотенузе, равна сумме половин площадей квадратов, построенных на катетах, а тогда и площади большого и двух малых квадратов равны. окажем теперь, что площадь треугольника ACK также равна половине площади квадрата DECA. Единственное, что необходимо для этого сделать, — это доказать равенство треугольников ACK и BDA (так как площадь треугольника BDA равна половине площади квадрата по указанному выше свойству). Равенство это очевидно, треугольники равны по двум сторонам и углу между ними. Именно — AB = AK, AD = AC — равенство углов CAK и BAD легко доказать методом движения: повернём треугольник CAK на 90° против часовой стрелки, тогда очевидно, что соответствующие стороны двух рассматриваемых треугольников совпадут (ввиду того, что угол при вершине квадрата — 90°).
окажем теперь, что площадь треугольника ACK также равна половине площади квадрата DECA. Единственное, что необходимо для этого сделать, — это доказать равенство треугольников ACK и BDA (так как площадь треугольника BDA равна половине площади квадрата по указанному выше свойству). Равенство это очевидно, треугольники равны по двум сторонам и углу между ними. Именно — AB = AK, AD = AC — равенство углов CAK и BAD легко доказать методом движения: повернём треугольник CAK на 90° против часовой стрелки, тогда очевидно, что соответствующие стороны двух рассматриваемых треугольников совпадут (ввиду того, что угол при вершине квадрата — 90°).

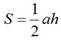 .
.

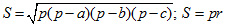
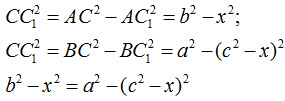




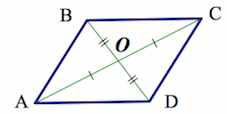 5. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам
5. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам

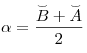 .
.
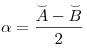 .
.
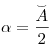 .
.

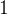 . Два угла вписанного в окружность четырехугольника равны
. Два угла вписанного в окружность четырехугольника равны 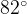 и
и  . Найдите больший из оставшихся углов. Ответ дайте в градусах.
. Найдите больший из оставшихся углов. Ответ дайте в градусах.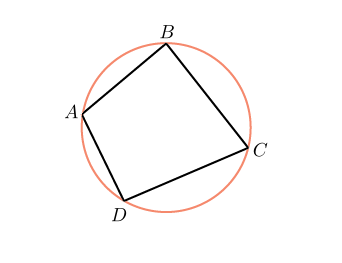
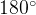 . Пусть угол
. Пусть угол  равен
равен 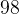 градусов. Если угол
градусов. Если угол 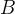 равен
равен  равен
равен 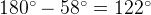 .
.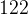 .
. . Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как
. Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как 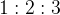 . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен
. Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 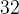 .
.
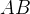 равна
равна 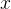 ,
,  равна
равна  , а
, а 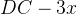 . По свойству описанного четырехугольника, суммы противоположных сторон равны, и значит,
. По свойству описанного четырехугольника, суммы противоположных сторон равны, и значит, 
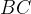 равна
равна  . Мы получаем, что
. Мы получаем, что 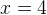 , а большая сторона равна
, а большая сторона равна  .
.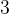 . Около окружности описана трапеция, периметр которой равен
. Около окружности описана трапеция, периметр которой равен 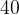 . Найдите ее среднюю линию.
. Найдите ее среднюю линию.
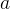 и
и  , а боковые стороны —
, а боковые стороны —  и
и 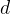 . По свойству описанного четырехугольника,
. По свойству описанного четырехугольника,  , и значит, периметр равен
, и значит, периметр равен 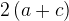 .
. 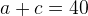 , а средняя линия равна
, а средняя линия равна 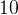 .
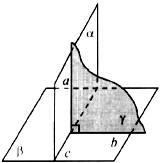
.







 =
=  α
α  (рис. 20).
(рис. 20).
 а. В плоскости а возьмем две пересекающиеся прямые а и b: а
а. В плоскости а возьмем две пересекающиеся прямые а и b: а 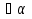 , b
, b  = В (рис.21.) Тогда по теореме 1 (§2, п.2.1.) через точку А можно провести прямые а1 и b1 такие, что а1 || а и b1 || b Отсюда по аксиоме CIII существует единственная плоскость
= В (рис.21.) Тогда по теореме 1 (§2, п.2.1.) через точку А можно провести прямые а1 и b1 такие, что а1 || а и b1 || b Отсюда по аксиоме CIII существует единственная плоскость 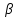 , проходящая через пересекающиеся прямые а1 и b1. Теперь остается показать, что α
, проходящая через пересекающиеся прямые а1 и b1. Теперь остается показать, что α  .
. 
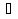 с и а
с и а  с = С.
с = С. α
α 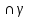 , b =
, b =  => а || b (рис. 22).
=> а || b (рис. 22). 
 Признак параллельности плоскостей
Признак параллельности плоскостей



