Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диагональ трапеции делит ее среднюю линию на отрезки, равные половинам оснований. ⇐ ПредыдущаяСтр 4 из 4
Задача 2. Основание AD трапеции ABCD на 6 см больше основания BC, а средняя линия равна 7 см. Найти длины отрезков, на которые диагональ AC делит среднюю линию. Решение: Рисунок — как и в задаче 1. Пусть BC=x см, тогда AD=x+6 см. По доказанному выше,
Ответ: 2 см, 5 см.
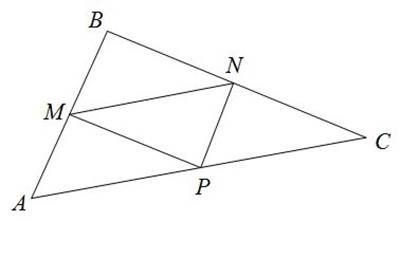
Средняя линия треугольника Средней линией треугольника называют такой отрезок, который соединяет середины двух сторон данного треугольника. В каждом треугольнике есть три средние линии, которые образуют еще один новый треугольник, расположенный внутри. Вершины вновь образованного треугольника находятся на срединах сторон данного треугольника. В каждом треугольнике есть возможность провести три средние линии. Свойства средней линии треугольника Каждая средняя линия треугольника, соединяющая середины его сторон, обладает следующими свойствами: 1. Средняя линия треугольника параллельна его третей стороне и равна её половине. Таким образом, мы видим, что сторона АС параллельна MN, которая в два раза меньше, чем сторона АС.
2. Средние линии треугольника делят его на четыре равных треугольника. Если мы посмотрим на треугольник АВС, то увидим, что средние линии MN, MP и NP разделили его на четыре равных треугольника, и в итоге образовались треугольники MBN, PMN, NCP и AMP. 3. Средняя линия треугольника отсекает от данного треугольника подобный, площадь которого равняется одной четвертой исходного треугольника. Так, например, в треугольнике АВС средняя линия MP отсекает от данного треугольника, образуя треугольник AMP, площадь которого равна одной четвертой треугольника АВС. 10Трапеция: теорема о четырех точках. Точки на сторонах треугольника
Теорема о четырех замечательных точках в трапеции. В любой трапеции точка пересечения диагоналей, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой. Теорема Фалеса.
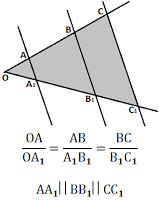
Если стороны угла пересечены параллельными прямыми, то отрезки, отсекаемые ими на одной стороне этого угла, пропорциональны соответственным отрезкам, отсекаемым ими на другой его стороне. Обратная теорема Фалеса. Если на одной стороне угла от его вершины O отложены отрезки OA, AB, BC,... и на другой его стороне также от вершины O отложены соответственно пропорциональные им отрезки OA1, A1B1, B1C1,... (OA/OA1= AB/AB2= BC/BC2=k), то прямые AA1, BB1, CC1, - параллельны.
Тренировочная работа №10 задание 16. Точки В1 и С1 лежат на сторонах соответственно AC и AB треугольника ABC, причем АВ1: В1С = АС1: С1В. Прямые ВВ1 и СС1 пересекаются в точке О. а) Докажите, что прямая АО делит пополам сторону BC. б) Найдите отношение площади четырехугольника АВ1ОС1 к площади треугольника ABC, если известно, что АВ1: В1С = АС1: С1В = 1:4.
Решение: а) Так как точки В1 и С1 делят стороны треугольника в одинаковых отношениях, то по теореме обратной теореме Фалеса прямая В1С1 всегда будет параллельна BC. Отсюда следует, что четырёхугольник ВСВ1С1 – трапеция. По теореме о четырех точках трапеции середины оснований, точка пересечения диагоналей и точка пересечения боковых сторон лежат на одной прямой. Таким образом, прямая АО проходит через середины оснований трапеции ВСВ1С1. б) Треугольник АВ1С1 подобен треугольнику АВС с коэффициентом подобия 1/5, следовательно, его площадь будет составлять 1/25 площади треугольника АВС или S/25. Тогда площадь трапеции ВСВ1С1 составляет 24/25 площади треугольника АВС, то есть 24S/25. Высота треугольника ВВ1С1, проведённая к стороне В1С1, равна высоте треугольника ВВ1С, проведённой к стороне ВС. Поскольку В1С1в пять раз меньше ВС, то площадь треугольника ВВ1С1в пять раз меньше, чем площадь треугольника ВВ1С1. Обозначим площадь треугольника ВВ1С1 – х, тогда площадь треугольника ВВ1С – 5 х. Значит, х + 5х = 24S/25, 6х = 24S/25, х = 4S/25. То есть площадь треугольника ВВ1С1 равна 4S/25, площадь треугольника ВВ1С равна 20S/25. Рассмотрим треугольники ВСС1 и ВСВ1. Так как у них общее основание – ВС, и одинаковая высота, то их площади равны. В состав каждого из них входит треугольник ОВС, поэтому площади треугольников ВВ1С1 и СВ1С1 равны, пусть они равны р.
Треугольники ОВ1С1 и ОВС подобны с коэффициентом подобия 1/5. Если обозначим площадь треугольника ОВ1С1 через а, то площадь треугольника ОВСравна 25 а. Так как площадь треугольника ВВ1С1 равна сумме площадей треугольников ВОС и В1ОС, получаем 4S/25 = а +р. Так как площадь треугольника ВВ1С равна сумме площадей треугольников ОВ1С1 и ВОС1, получаем 20S/25 =25 а +р. Вычитая из этого равенства предыдущее, получаем 16S/25 =24а. Отсюда а = 2S/75. Площадь четырехугольника АВ1ОС1 = S/25 +2S/75 = S/15 Ответ: 1:15.
11Вывод формул площадей параллелограмма, треугольника и трапеции. Площадь треугольника, трапеции, параллелограмма · Площадь треугольника равна половине произведения основания треугольника на высоту. · Площадь трапеции равна произведению полусуммы его оснований на высоту. · Площадь параллелограмма равна произведению его основания на высоту.
Используя рисунки выше, необходимо вспомнить, как доказывается утверждение, что «Если а является основанием треугольника, h — проведенная к нему высота, S — площадь треугольника, то
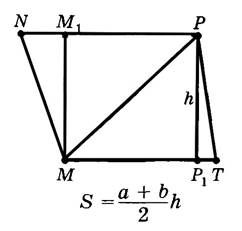
С помощью рисунка выше вспомните доказательство утверждения: «Если а и b — основания трапеции, h — ее высота, S — площадь трапеции, то
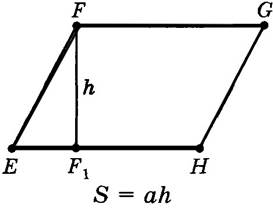
Используя данное утверждение о площади трапеции и рисунок ниже, вспомните доказательство утверждения: «Если а — основание параллелограмма, h — проведенная к нему высота, S — площадь параллелограмма, то S = ah».
Формула Герона Теорема: Если а, b с — стороны треугольника, р — полупериметр, р=(a+b+c)/2, r — радиусвписанной окружности, S — площадь треугольника, то:
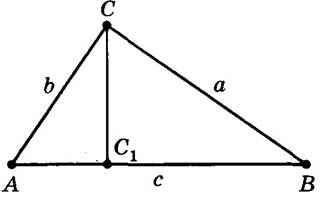
Доказательство. Пусть а, b, с — длины сторон ВС, АС, АВ треугольника ABC (рисунок).
Проведем высоту CC1 и обозначим х длину отрезка АС1. Тогда ВС1=с-х. По теореме Пифагора получаем:
Решим это уравнение и найдем х:
Тогда:
Данная формула называется формулой Герона. Герон Александрийский (I в.) — древнегреческий ученый, который работал в Александрии. Математические работы Герона являются энциклопедией античной практической математики.
Определение параллелограмма
Параллелограмм – четырехугольник, у которого противоположные стороны попарно параллельны.
Частные случаи параллелограмма: ромб, прямоугольник, квадрат. Свойства параллелограмма
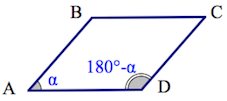
1. Противоположные стороны параллелограмма попарно равны 2. Противоположные углы параллелограмма попарно равны
3. Сумма смежных (соседних) углов параллелограмма равна 180 градусов 4. Сумма всех углов равна 360°
6. Точка пересечения диагоналей является центром симметрии параллелограмма
7. Диагонали параллелограмма и стороны
8. Биссектриса отсекает от параллелограмма равнобедренный треугольник
Признаки параллелограмма
Четырехугольник является параллелограммом, если выполняется хотя бы одно из следующих условий: 1. Противоположные стороны попарно равны: 2. Противоположные углы попарно равны: 3. Диагонали пересекаются и в точке пересечения делятся пополам 4. Противоположные стороны равны и параллельны:
5.
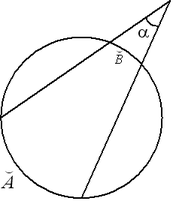
14 Углы, связанные с окружностью
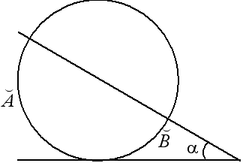
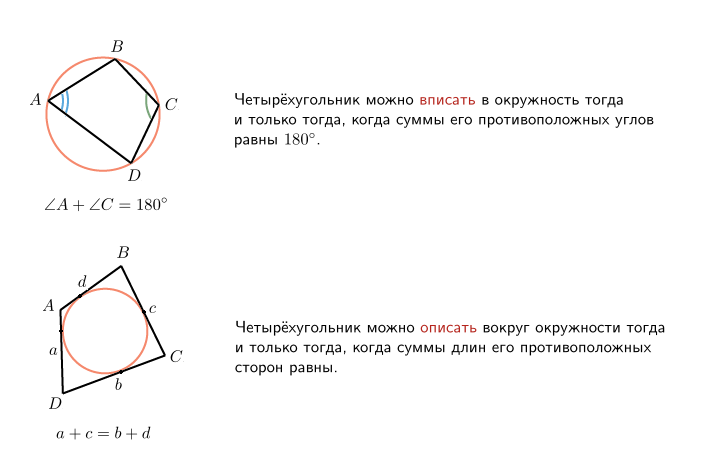
15-16 15Вписанные и 16описанные четырехугольники Вписанный четырехугольник — четырехугольник, все вершины которого лежат на одной окружности. Описанный четырехугольник — такой, что все его стороны касаются одной окружности. В этом случае окружность вписана в четырехугольник. На рисунке — вписанные и описанные четырехугольники и их свойства.
Посмотрим, как эти свойства применяются в решении задач ЕГЭ.
Сумма противоположных углов вписанного четырехугольника равна Ответ:
Пусть сторона Ответ:
Мы помним, что средняя линия трапеции равна полусумме оснований. Пусть основания трапеции равны Еще раз повторим свойства вписанного и описанного четырехугольника.
Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы его противоположных углов равны Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы длин его противоположных сторон равны. Докажите эти утверждения. Это задание особенно полезно тем, кто нацелен на решение части С.
Признаки параллельности прямой и плоскости:
1) Если прямая, лежащая вне плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельна этой плоскости.
2) Если прямая и плоскость перпендикулярны одной и той же прямой, то они параллельны.
Признаки параллельности плоскостей:
1) Если две пересекающиеся прямые одной плоскости cоответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
2) Если две плоскости перпендикулярны одной и той же прямой, то они параллельны.
Признаки перпендикулярности прямой и плоскости:
1) Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.
2) Если плоскость перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.
Наклонная к плоскости. Прямая, пересекающая плоскость и не перпендикулярная ей, называется наклонной к плоскости.
Теорема о трёх перпендикулярах. Прямая, лежащая в плоскости и перпендикулярная проекции наклонной к этой плоскости, перпендикулярна и самой наклонной.
Признаки параллельности прямых в пространстве:
1) Если две прямые перпендикулярны одной и той же плоскости, то они параллельны.
2) Если в одной из пересекающихся плоскостей лежит прямая, параллельная другой плоскости, то она параллельна линии пересечения плоскостей.
Признак перпендикулярности плоскостей: если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Теорема об общем перпендикуляре к двум скрещивающимся прямым. Для любых двух скрещивающихся прямых существует единственный общий перпендикуляр.
Геометрия Перпендикулярность двух плоскостей
Определение: две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения плоскостей, пересекает их по перпендикулярным прямым.
|
||||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 1346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.146.223 (0.073 с.) |
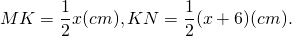

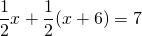
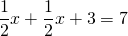


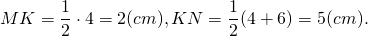

 Прежде чем перейти к решению следующей задачи вспомним ещё несколько теорем планиметрии.
Прежде чем перейти к решению следующей задачи вспомним ещё несколько теорем планиметрии.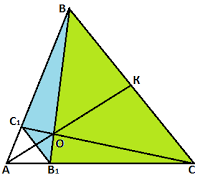

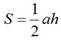 .
.

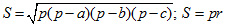
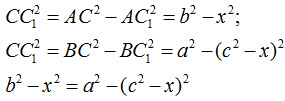




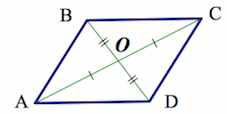 5. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам
5. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам
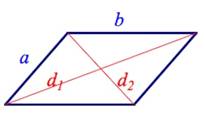

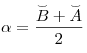 .
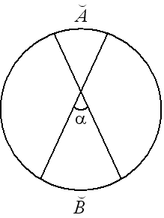
.
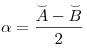 .
.
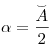 .
.

 . Два угла вписанного в окружность четырехугольника равны
. Два угла вписанного в окружность четырехугольника равны 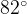 и
и  . Найдите больший из оставшихся углов. Ответ дайте в градусах.
. Найдите больший из оставшихся углов. Ответ дайте в градусах.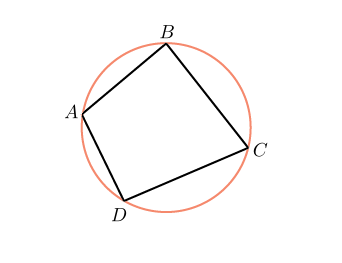
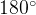 . Пусть угол
. Пусть угол  равен
равен 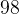 градусов. Если угол
градусов. Если угол 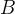 равен
равен  равен
равен 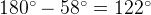 .
.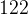 .
. . Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как
. Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как 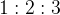 . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен
. Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 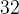 .
.
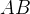 равна
равна 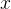 ,
,  равна
равна  , а
, а 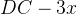 . По свойству описанного четырехугольника, суммы противоположных сторон равны, и значит,
. По свойству описанного четырехугольника, суммы противоположных сторон равны, и значит, 
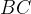 равна
равна  . Мы получаем, что
. Мы получаем, что 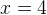 , а большая сторона равна
, а большая сторона равна  .
.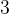 . Около окружности описана трапеция, периметр которой равен
. Около окружности описана трапеция, периметр которой равен 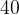 . Найдите ее среднюю линию.
. Найдите ее среднюю линию.
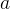 и
и  , а боковые стороны —
, а боковые стороны —  и
и 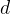 . По свойству описанного четырехугольника,
. По свойству описанного четырехугольника,  , и значит, периметр равен
, и значит, периметр равен 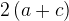 .
. 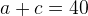 , а средняя линия равна
, а средняя линия равна 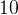 .
.