Структура твердого тела и температура плавления

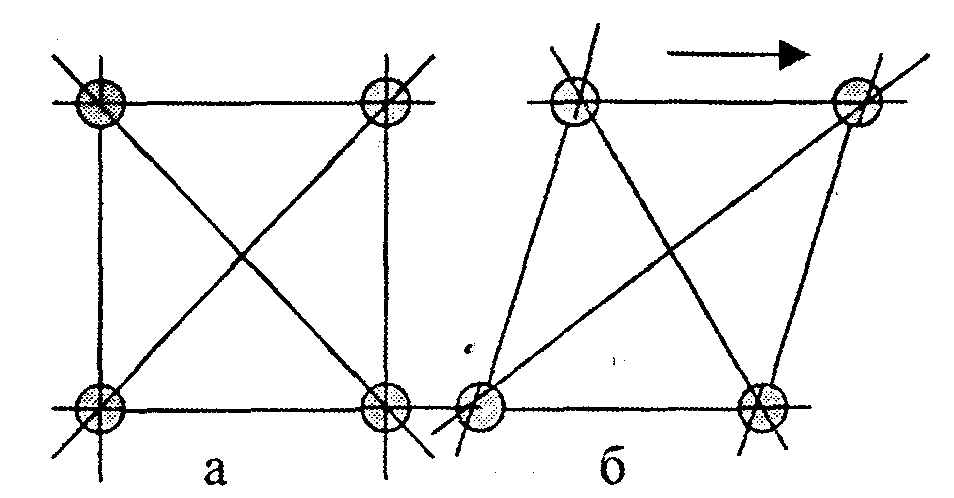
Напомним, что структура есть результат совокупного действия химических связей, обеспечивающих единое целое. Поэтому проч­ность структуры твердого тела зависит от прочности химических связей, так же, как прочность здания зависит от того, из каких кир­пичиков оно построено и каким раствором связаны эти кирпичики.

У различных групп веществ и соединений для создания опти­мальной структуры имеются определенные условия и особенности. Так, для класса оксидов металлов одной и той же группы или с оди­наковой валентностью металла можно отметить следующие особен­ности:

- температура плавления оксида тем выше, чем выше координа­ционное число (к.ч.) катиона;

- температура плавления оксида снижается по мере уменьшения к.ч. металла по отношению к кислороду;

- температура плавления оксида снижается при уменьшении к.ч. кислорода при неизменном к.ч. ионов металла, равном 6 (пример: к.ч. MgO (2800°С) > к.ч. А1₂О₃(2050°С) > к.ч. ТiO₂(1840°С);

- температура плавления оксида тем выше, чем выше плотность
упаковки ионов (т.е. выше к.ч. ионов) и выше прочность химической
связи.

Взаимосвязь "температура плавления - тепловое расширение "

Анализ механизмов теплового расширения и плавления, а также влияния на них состава, химических связей и структуры тела выяв ляет в указанных процессах много общего. Особенно это относится к влиянию типа химической связи и ее прочности на интенсивность и результат рассматриваемых процессов.

С увеличением прочности химической связи КТР тел уменьша­ется (см. табл. 4.3), а их температура плавления растет (см. табл.4.8). Эта взаимосвязь свидетельствует о том, что температура плавления может служить косвенной характеристикой процесса теплового расширения кристаллических тел.

Лекция 5. ДЕФОРМАТИВНЫЕ И ПРОЧНОСТНЫЕСВОЙСТВА МАТЕРИАЛОВ

Деформативные свойства

Основные понятия, термины, определения

Деформативные свойства материалов проявляются при воздействии на них механических и термических нагрузок, в результате которых в материале возникают различного рода деформации, напряженное состояние и, наконец, наступает разрушение.

Деформация — это нарушение взаимного расположения множества частиц материальной среды, которое приводит к изменению формы и размеров тела и вызывает изменение сил взаимодействия между частицами, т.е. возникновение напряжений. Заметим, что чаще деформации вызывают напряжения, и поэтому, как правило, строят графики зависимости напряжений от деформаций, а не наоборот.

Простейшими элементами деформации являются относительное удлинение и сдвиг.

Относительное удлинениё «ε» стержня или материального волокна среды длины «l» есть отношение изменения (l - l_o) к первоначальной длине: ε = (l-l_o)/l_o.

Сдвигом называется изменение угла у между элементарными волокнами, исходящими из одной точки и образующими прямой угол до деформации (см. рис. 5.1).

В твердых телах деформация называется упругой, если она исчезает после снятия нагрузки, и пластической, если она после снятия нагрузки не исчезает; если она исчезает не полностью, то называется упругопластической, если она изменяется во времени и обратима, то называется вязкоупругой.

Разрушение — это ослабление взаимосвязи между частицами при нарушении сплошности структуры.

Различают хрупкое, т.е. мгновенное (без деформации) и пластическое (с деформацией) разрушение твердого тела.

Таким образом, к этой группе свойств можно отнести упругость, пластичность, хрупкость, вязкость, прочность и твердость.

Упругость

Упругость — свойство изменять форму и размеры под действием нагрузок и самопроизвольно восстанавливать исходную конфигурацию при прекращении внешних воздействий.

Упругость тел обусловлена силами взаимодействия атомов, из которых они построены. В твердых телах при температуре абсолютного нуля и отсутствии внешних воздействий атомы занимают равновесное положение, в котором сумма всех сил, действующих на каждый атом со стороны остальных, равна нулю, а потенциальная энергия атома минимальна.

Под влиянием внешних воздействий атомы смещаются относительно своих равновесных положений, что сопровождается увеличением потенциальной энергии тела на величину, равную работе внешних сил на изменение формы и объема тела. В результате возникают напряжения, величины которых пропорциональны произведенной деформации.

Пока отклонения межатомных расстояний и валентных углов от их равновесных значений малы, они пропорциональны силам межатомного взаимодействия, подобно тому, как удлинение или сжатие пружины пропорционально приложенной силе. Поэтому упругое тело можно представить как совокупность атомов-шариков, соединенных пружинами, ориентации которых фиксированы другими пружинами (рис. 5.1), а константы упругости пружин модели подобны модулю упругости материала.

Рис. 5.1. Шариковая модель элементарной ячейки кубического кристалла:

а - в равновесии при отсутствии внешних сил;

б - под действием внешних сил и касательных напряжений

 

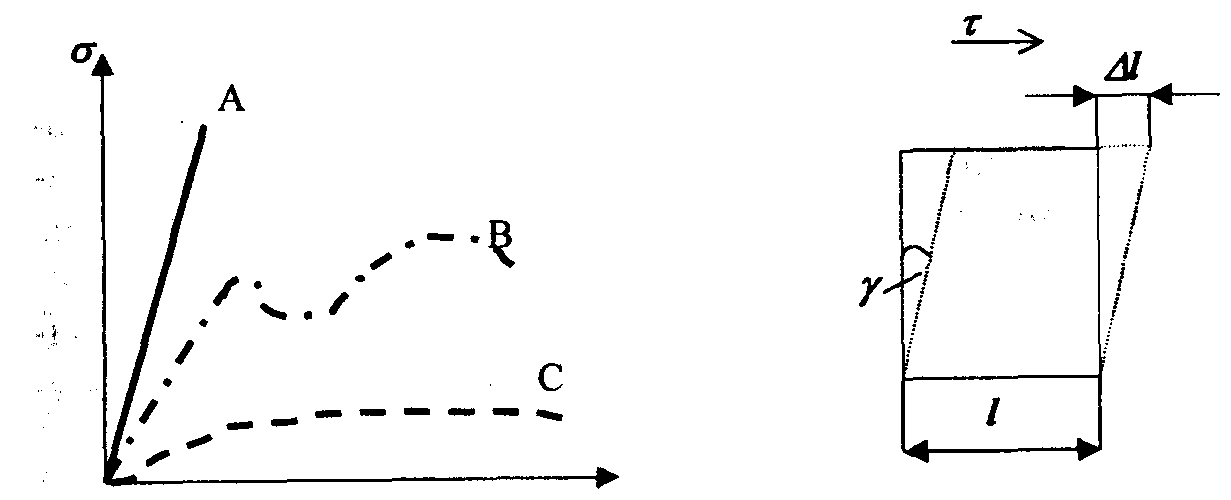
Поле снятия нагрузки конфигурация упругого деформированного тела с неравновесными межатомными расстояниями и валентными углами оказывается неустойчивой и самопроизвольно возвращается в равновесное состояние. Запасенная в теле избыточная потенциальная энергия превращается в кинетическую энергию колеблющихся атомов, т.е. в теплоту.

Константы упругости

Количественно упругость характеризуется константами, свойственными каждому материалу. При этом необходимо учитывать, что большинство свойств, кроме плотности и теплоемкости, связано с анизотропией структуры. Упругость является ярко выраженным анизотропным свойством. Поэтому следует различать упругость кристаллов и анизотпропных материалов и упругость изотропных тел.

Поликристаллические тела и материалы в целом изотропны, анизотропия их свойств проявляется только в результате формования или обработки, например прессования, штампования, прокатки, уплотнения и т.п. Таким образом, формируется анизотропия свойств керамической плитки, черепицы, стального листа и т.д. В дальнейшем рассматривается упругость только изотропных свойств, для которых не применимы представления об ориентированных кристаллографических осях и пр.

С учетом вышеизложенного для большинства природных и искусственных материалов (горные породы, керамика, бетон, металлы и т.д.) при малых деформациях зависимости между напряжениями «σ» и деформациями «ε» можно считать линейными (рис. 5.2) и описывать обобщенным законом Гука:

σ = Еε,

где Е — модуль упругости (модуль Юнга).

Подобным образом напряжение сдвига «τ» прямо пропорционально относительной деформации сдвига или углу сдвига у(рис. 5.3):

τ = G. у

где G — модуль сдвига.

о.

Рис. 5.2. Классическая зависимость напряжение — деформация:

А — керамики; В — металлов; С — полимеров

Рис. 5.3. Упругая деформация твердого тела при сдвиге

 

Удлинение образца при растяжении сопровождается уменьшением его толщины (рис. 5.4). Относительное изменение толщины Δl/l к относительному изменению длины Δd/d называется коэффициентом Пуассона «μ» или коэффициентом поперечного сжатия:

μ = (Δl/l) / (Δd/d).

 

Рис. 5.4. Упругая деформация твердого тела при растяжении

 

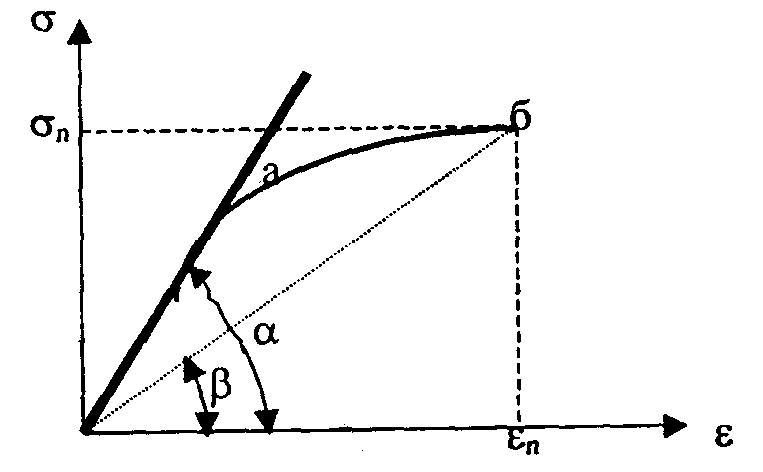
Если при деформации тела его объем не изменяется, а это может иметь место только при пластическом или вязком течении, то μ = 0,5. Однако, практически, эта величина значительно ниже теоретического показателя и для разных материалов она различна. Упругие материалы (бетон, керамика и др.) имеют невысокие значения коэффициента Пуассона (0,15-0,25), пластичные (полимерные материалы) — более высокие (0,3-0,4). Это объясняется зависимостью между силами притяжения и отталкивания и изменением межатомного расстояния при деформации.

Модуль Юнга

Модуль Юнга, или модуль продольной деформации Е показывает критическое напряжение, которое может иметь структура материала при максимальной ее деформации до разрушения; имеет размерность напряжений (МПа).

Е =σ_р/ε;

Где: σ_р – критическое напряжение.

У поликристаллических материалов обычно наблюдаются отклонение от линейной σ = ƒ(ε,), несвязанное с энергией кристаллической решетки, а зависящей от структуры материала. Для оценки упругих свойств таких материалов применяют два модуля упругости: касательный Е = tgα и секущий V= tgβ, который называют модулем деформаций (рис. 5.5).

 

Рис. 5.5. Схематическое изображение деформации огнеупоров:

а — кривая деформации; б — точка разрушения;

σ; — предельное напряжение при разрушении; ε — деформация

 

Величина модуля упругости двухфазной системы является средней между величинами модулей упругости каждой из фаз, и аналитическое выражения для ее нахождения аналогичны тем, что используются при различных значениях линейного КТР:

Е = Е₁V₁ + E₂V₂,

где V₁ и V₂ — относительные объемные доли первой и второй фаз.

Это соотношение используется при разработке стеклопластиков, т.е. пластмасс, армированных стекловолокном. Е стекловолокна (~7^.10⁴ МПа) велик по сравнению с Е пластмасс (Е = 0,7^.10⁴ МПа). Поэтому даже при низкой объемной доле стекловолокна в композиции на него как на более прочный компонент приходится большая часть общей нагрузки.

Пористость и модуль Юнга

Увеличение пористости структуры снижает ее модуль упругости, так как пористость представляет собой вторую или п -ю фазу с минимальным модулем упругости. Количественно эта зависимость представляется достаточно сложной, так как кроме суммарного объема пор необходимо учитывать их форму, непрерывность, извилистость и пр. Если принять, коэффициент Пуассона μ равным 0,3, то величина модуля упругости пористого тела в случае наличия замкнутых пор в непрерывной среде достаточно точно может быть определена по следующему эмпирическому уравнению:

Е = Е_о (1-1,9П+0,9П²),

где Е и Е_о — модули упругости пористого и абсолютно плотного тела;

П — относительная пористость, ед.

Если в пористых материалах пространство пор непрерывно, а твердые частицы могут смещаться относительно друг друга, то влияние пористости оказывается более значительным, чем в результате определения по приведенному уравнению.