
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормальное состояние атома водорода. Полная волновая функция и полный набор наблюдаемых невозбужденного состояния атома водорода. ⇐ ПредыдущаяСтр 3 из 3
Нормальным состоянием атома водорода называется состояние с наименьшим значением полной энергии. Такое состояние возникает при квантовых числах
где нормировочный коэффициент
Подставим квантовые числа (*) в (2) – (4) и получим:
Таким образом, полная функция нормального состояния атома водорода имеет вид:
Численные коэффициенты
Вычисление интегралов (10) и (11) приводит к следующим результатам:
Окончательно:
Учитывая, что полная энергия атома водорода
получаем для невозбужденного состояния атома водорода:
2)Дать названия элементам, входящие в формулы:
Присоединенный полином Лежандра. Волновая функция, являющаяся решением сферическое уравнение Шредингера для атома водорода, имеет вид:
Как видно из (1), эта функция содержит полином. Коэффициенты
Таким образом, явный вид всех коэффициентов можно установить через первый. Первый же коэффициент
В этом случае вместо полинома
где
В (5) общий нормировочный коэффициент
и имеет вид:
Билет №25 1)
2)Дать названия элементам, входящие в формулы:
Воспользуемся ранее полученным из стационарного уравнения Шредингера для атома водорода сферическим уравнением Лагранжа:
Введем обозначение:
После разделения переменных уравнение (1) разбивается на два:
В (3) и (4) m –постоянная величина, которая устанавливается в процессе решения уравнения (3) и называется квантовым магнитным орбитальным числом электрона в атоме водорода. Решим уравнение (4). Распишем подробно:
Подставим (5) в (4):
Разделим левую правую части (6) на выражение
При
Дифференцируя (8) и подставляя результат в (7), получаем уравнение:
Для устранения
Т.к. число m может принимать отрицательные значения, то его величина берется по модулю в силу условия Тогда (9) принимает вид:
Далее решение (11) отыскивается в виде ряда
Дифференцируем (12), результат подставляем в (11) и объединяем слагаемые с одинаковыми степенями косинусов:
Равенство (13) выполняется, если коэффициенты при всех степенях
Остальные коэффициенты находятся аналогично (15):
Выражение (16) представляет собой рекуррентную формулу, позволяющую вычислить последующий коэффициент
Тогда
3)
Билет №26 1) Угловое распределение плотности электронного облака в атоме водорода.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 233; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.219.217 (0.016 с.) |
 Рассмотрим полную волновую функцию электрона в атоме водорода, заданную в сферических координатах без учета ее зависимости от времени:
Рассмотрим полную волновую функцию электрона в атоме водорода, заданную в сферических координатах без учета ее зависимости от времени: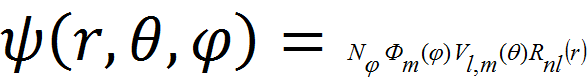 ,
,
 при любых квантовых числах;
при любых квантовых числах;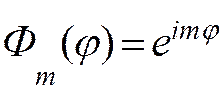


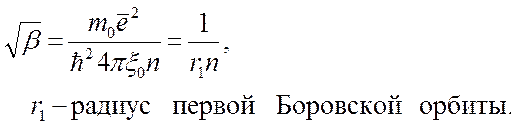

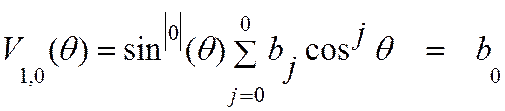


 определяются из условия нормировки волновой функции:
определяются из условия нормировки волновой функции:

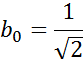


 , его механический орбитальный момент импульса
, его механический орбитальный момент импульса  и проекция механического орбитального момента импульса на ось z
и проекция механического орбитального момента импульса на ось z 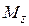 соответственно равны:
соответственно равны: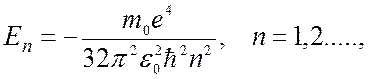
 ,
,






 полинома устанавливаются через предыдущие коэффициенты
полинома устанавливаются через предыдущие коэффициенты  с помощью рекуррентной формулы
с помощью рекуррентной формулы
 будет в конечном итоге играть роль нормировочного коэффициента и определяться из условия нормировки. Однако, можно упростить получение полинома в (1) и вместо поиска нормировочных коэффициентов для
будет в конечном итоге играть роль нормировочного коэффициента и определяться из условия нормировки. Однако, можно упростить получение полинома в (1) и вместо поиска нормировочных коэффициентов для  установить формулу для общего нормировочного коэффициента. Для этого коэффициент
установить формулу для общего нормировочного коэффициента. Для этого коэффициент  представляют в виде:
представляют в виде:
 получается полином
получается полином  вида:
вида:
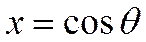 . Сферическая функция (1) при этом принимает вид:
. Сферическая функция (1) при этом принимает вид:
 устанавливается из условия нормировки
устанавливается из условия нормировки





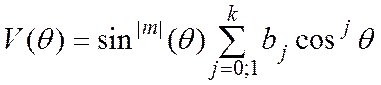







 . В результате получим:
. В результате получим:
 знаменатели в (7) обращаются в
знаменатели в (7) обращаются в  и (7) теряет смысл. Следовательно, функция
и (7) теряет смысл. Следовательно, функция  должна содержать в качестве сомножителя синус:
должна содержать в качестве сомножителя синус:

 в знаменателе (9) (причину этого смотри выше) полагаем
в знаменателе (9) (причину этого смотри выше) полагаем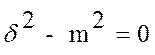 , откуда следует:
, откуда следует:
 .
.

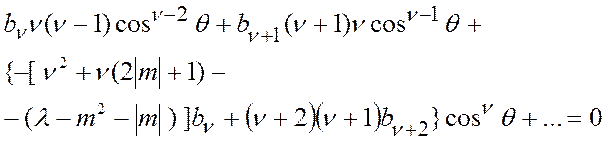
 равны нулю. Приравнивая к нулю эти коэффициенты, получаем:
равны нулю. Приравнивая к нулю эти коэффициенты, получаем:


 через предыдущий
через предыдущий  . Из (16) следует, что ряд (12) может содержать либо четные степени косинусов
. Из (16) следует, что ряд (12) может содержать либо четные степени косинусов  , либо нечетные
, либо нечетные  . В общем виде (12) принимает вид:
. В общем виде (12) принимает вид:








