
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Привести и проанализировать конечные результаты решения сферического и радиального уравнения Шредингера.
Стационарное уравнение Шредингера для атома водорода разделяется на два уравнения: 1) сферическое:
2) радиальное:
Уравнение (1) хорошо известно в математике (см. любой курс методов математической физики, раздел «Уравнение Лапласа в сферических координатах»). Искомые решения
где
Нормировочный множитель в формуле (3) определяется из условия нормировки:
Из уравнения (2) устанавливается явный вид радиальных функций:
где Коэффициенты
где Кроме того, из (2) следует:
Решение уравнения (1) приводит к количественным результатам:
Выше приведены следующие обозначения для физических величин, описывающих состояние электрона в атоме водорода: 2). №15.Для δ – функции Дирака закончить равенства: 1) 3) 1)
3).
Билет №16 1). Разделить переменные Воспользуемся ранее полученным из стационарного уравнения Шредингера для атома водорода сферическим уравнением Лагранжа:
Введем обозначение:
С учетом (2) уравнение (1) принимает вид:
Уравнение (3) решаем методом разделения переменных. Для этого представим сферическую функцию
Выражение (4) подставим в (3), вынося за знак производных функции, на которые производные не действуют:
Разделим левую и правую части (5) на выражение
Как видно из (6), левая и правая части этого уравнения зависят от разных переменных
2). Доказать правомерность представления δ-функции Дирака в виде
Как известно, δ -функцией Дирака называют функцию δ (β), удовлетворяющую следующим условиям:
Из (1) следует, что функция δ (β) носит резко выраженный сингулярный характер. Качественно ее можно представить себе равной нулю всюду, кроме точки β = 0, а в этой точке настолько большой, что площадь, ограниченная графиком этой функции и осью β, конечна и равна единице. Весьма полезным оказывается одно частное представление δ (β) в виде предельного значения функции
3).
Билет №17 1) Установить зависимость сферической функции атома водорода от азимутального угла Решим уравнение, полученное после разделения переменных в сферическом уравнении Шредингера для атома водорода:
Уравнение (1) является линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Как известно из математического анализа решение такого уравнения отыскивается в виде
Учитывая периодичность функции (2)
можно установить возможные значения числа m:
Легко проверить, что (2) является собственной функцией оператора проекции механического орбитального момента импульса
Число m носит название квантового магнитного орбитального числа 2) Охарактеризовать элементы, входящие в формулу для волнового пакета свободной частицы Как известно, понятие дисперсии сводится к понятию среднеквадратичного отклонения рассматриваемой величины от его среднего значения. В частности, дисперсия координаты задается выражением
а дисперсия импульса -
Рассмотрим эти понятия (
а неопределенности координаты и импульса были бы минимальными, т.е.
Можно показать, что этим требованиям отвечает функция
Она нормирована в соответствии с общим правилом нормировки
И нормировочный коэффициент равен величине Пользуясь определением среднего в квантовой механике
Из (7) следует
Отсюда видно, что выбранная волновая функция (5) обладает уникальным свойством – она минимизирует соотношение неопределенностей Гейзенберга, приводя к равенству (4), т.к. (8) тождественно (4). Из (7) видно, что квадрат величины b, входящей в нормировочный коэффициент волновой функции (5) имеет смысл удвоенной дисперсии координаты свободной частицы в начальный момент времени. Можно показать, что состояние с волновой функцией (5) не является стационарным и энергия не имеет определенного значения. Такое нестационарное состояние частицы, довольно четко локализованное в пространстве, является примером пространственного волнового пакета. 3)
Билет №18 1) Установить зависимость сферической функции атома водорода от полярного угла Воспользуемся ранее полученным из стационарного уравнения Шредингера для атома водорода сферическим уравнением Лагранжа:
Введем обозначение:
После разделения переменных уравнение (1) разбивается на два:
В (3) и (4) m –постоянная величина, которая устанавливается в процессе решения уравнения (3) и называется квантовым магнитным орбитальным числом электрона в атоме водорода. Решим уравнение (4). Распишем подробно:
Подставим (5) в (4):
Разделим левую правую части (6) на выражение
При
Дифференцируя (8) и подставляя результат в (7), получаем уравнение:
Для устранения
Т.к. число m может принимать отрицательные значения, то его величина берется по модулю в силу условия
Тогда (9) принимает вид:
Далее решение (11) отыскивается в виде ряда
Дифференцируем (12), результат подставляем в (11) и объединяем слагаемые с одинаковыми степенями косинусов:
Равенство (13) выполняется, если коэффициенты при всех степенях
Остальные коэффициенты находятся аналогично (15):
Выражение (16) представляет собой рекуррентную формулу, позволяющую вычислить последующий коэффициент
Тогда
2) Доказать свойство δ – функции Дирака:
Чисто формально δ-функцией называется функция δ(х), удовлетворяющая следующим требованиям:
Конечно, такая функция выходит за рамки величин, рассматриваемых в классическом анализе. Наглядно δ-функцию можно представлять себе следующим образом. Рассмотрим обычную функцию, которая всюду равна нулю, кроме малого интервала Δх, включающего точку x = 0. Если теперь стремить размеры этого интервала к нулю, одновременно увеличивая значение функции внутри него так, чтобы площадь под ее графиком все время оставалась равной единице, то «в пределе» мы и получим δ -функцию. Одно из наиболее важных свойств δ-функции, которое математики и положили в основу ее строгого определения, состоит в том, что для любой непрерывной функции f (x) имеем
Докажем (3). Действительно, для значений х за пределами сколь угодно малого интервала, содержащего точку х = 0, δ-функция равна нулю, благодаря чему в левой части (3) можно
3).
Билет №19 1) Рассчитать максимальный номер слагаемого полинома Ряд (17) не может содержать бесконечное число слагаемых, т.к. в противном случае функция
Или:
Обозначив
Получаем
Из (20) следует
Т.к. Из (2) следует
И окончательно для волновой функции
2) Определить явление, описываемое формулой
Прохождением частиц через потенциальные барьеры объясняется целый ряд физических явлений: внешняя контактная разность потенциалов при соприкосновении разнородных проводников, холодная эмиссия электронов (испускание электронов с поверхности проводнка при напряженности электрического поля вблизи этой поверхности свыще ~ 100 кэВ/см), некоторые ососбенности ядерных реакций (например попадание протона внутрь ядра извне при его кинетической энергии, меньшей чем энергия электрического отталкивания ядра атома), спонтанный α – распад радиоактивных ядер и др. 3)
Билет №20 1) Присоединенный полином Лежандра. Общий вид нормировочного коэффициента сферической функции атома водорода, заданной через полином Лежандра. Волновая функция, являющаяся решением сферическое уравнение Шредингера для атома водорода, имеет вид:
Как видно из (1), эта функция содержит полином. Коэффициенты
Таким образом, явный вид всех коэффициентов можно установить через первый. Первый же коэффициент
В этом случае вместо полинома
где
В (5) общий нормировочный коэффициент
и имеет вид:
2)Пояснить рисунок
Зависимость потенциальной энергии U (r) α - частицы от ее расстояния r до центра ядра энергии приближенно представлен в виде потенциальной ямы с вертикальными стенками. При r > R, когда на α - частицу действуют только силы электрического отталкивания, ход потенциальной энергии определяется формулой для энергии взаимодействия двух точечных электрических зарядов:
Здесь Z – порядковый номер материнского ядра, а
3)
Билет №21
1) Решение радиального уравнения Шредингера. Полная энергия атома водорода. Главное квантовое число. Деление переменных в стационарном уравнении Шредингера для атома водорода
заданном в сферической системе координат, приводит к разделению (1) на три уравнения, каждое из которых зависит от своей переменной. Уравнение, зависящее от радиуса r, называется радиальным уравнением и имеет вид:
где
Учтем, что
Беря производные в (4) и проводя преобразования, получаем:
Введем обозначения:
После подстановки (6) и
Решение уравнения (7) отыскивается в виде произведения двух функций
где
Тогда
Функция
где
где
Пояснить формулу
число соударений α – частицы со стенками потенциальной ямы в единицу времени равно
Для получения коэффициента D прохождения через потенциальный барьер воспользуемся теорией потенциальных барьеров произвольной формы:
При наших не претендующих на большую точность расчетах можно принять, что
Логарифмируя формулу (1), получим с учетом выражений (4), (5) и (7):
Эта формула устанавливает искомую связь между свойствами ядра (величиной R, зависящей от радиуса ядра, и его порядковым номером Z), энергией α – частицы Е и постоянной распада λ. В частности она подтверждает закон Гейгера – Нэттола
3)
Билет №22
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 291; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.24.159 (0.099 с.) |


 уравнения (1) называются сферическими функциями. Они зависят от целых чисел l и m, что отражено в их символическом обозначении. Эти функции имеют явный вид:
уравнения (1) называются сферическими функциями. Они зависят от целых чисел l и m, что отражено в их символическом обозначении. Эти функции имеют явный вид:
 - присоединенный полином Лежандра от аргумента cos θ вычисляется по формуле:
- присоединенный полином Лежандра от аргумента cos θ вычисляется по формуле:
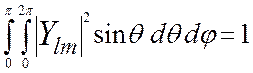

 , r 1- радиус первой Боровской орбиты, i = 0,1,2,...
, r 1- радиус первой Боровской орбиты, i = 0,1,2,... вычисляются из рекуррентной формулы, полученной из решения радиального уравнения (2):
вычисляются из рекуррентной формулы, полученной из решения радиального уравнения (2):
 ,
,  .
.
 ,
,

 - полная энергия,
- полная энергия,  - орбитальный механический момент импульса и его проекция на ось z соответственно, n - главное квантовое число,
- орбитальный механический момент импульса и его проекция на ось z соответственно, n - главное квантовое число,  - механическое орбитальное квантовое число, m – магнитное орбитальное квантовое число.
- механическое орбитальное квантовое число, m – магнитное орбитальное квантовое число. 2)
2) 
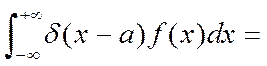 4)
4) 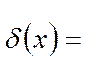 5)
5) 
 2)
2)  3)
3) 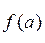 4)
4)  5)
5) 

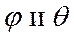 в сферическом уравнении Шредингера для атома водорода.
в сферическом уравнении Шредингера для атома водорода.


 в виде произведения
в виде произведения

 и преобразуем его:
и преобразуем его:
 Такое равенство выполняется лишь при условии, что каждая часть независимо друг от друга равна общей постоянной величине. Обозначим ее
Такое равенство выполняется лишь при условии, что каждая часть независимо друг от друга равна общей постоянной величине. Обозначим ее  . Тогда (6) разбивается на два независимых уравнения:
. Тогда (6) разбивается на два независимых уравнения:

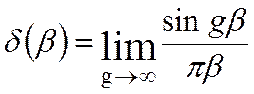

 где g – положительное вещественное число. Эта функция, равная
где g – положительное вещественное число. Эта функция, равная  при β = 0 при увеличении
при β = 0 при увеличении  осциллирует с постоянно убывающей амплитудой и с периодом
осциллирует с постоянно убывающей амплитудой и с периодом  а интеграл от нее по β, взятый в пределах
а интеграл от нее по β, взятый в пределах  равен единице независимо от значения g. Поэтому предел
равен единице независимо от значения g. Поэтому предел  при
при  имеет все свойства δ - функции; при β = 0 он становится бесконечно большим, интеграл от предельного выражения равен единице, а бесконечно быстрые осцилляции при увеличении
имеет все свойства δ - функции; при β = 0 он становится бесконечно большим, интеграл от предельного выражения равен единице, а бесконечно быстрые осцилляции при увеличении  означают, что весь вклад в интеграл, содержащий эту функцию, обусловлен бесконечно малой окрестностью точки β = 0. В связи с этим можно положить
означают, что весь вклад в интеграл, содержащий эту функцию, обусловлен бесконечно малой окрестностью точки β = 0. В связи с этим можно положить

 . Вычислить величину проекции орбитального механического момента импульса
. Вычислить величину проекции орбитального механического момента импульса  и возможные значения магнитного орбитального квантового числа m электрона в атоме водорода.
и возможные значения магнитного орбитального квантового числа m электрона в атоме водорода.
 с помощью характеристического уравнения
с помощью характеристического уравнения  В конечном итоге искомая функция с точностью до постоянного коэффициента оказывается равной:
В конечном итоге искомая функция с точностью до постоянного коэффициента оказывается равной:


 . Действительно,
. Действительно,  , откуда следует, что
, откуда следует, что  является собственным значением оператора проекции механического орбитального момента импульса на ось z
является собственным значением оператора проекции механического орбитального момента импульса на ось z  , т.е.
, т.е.
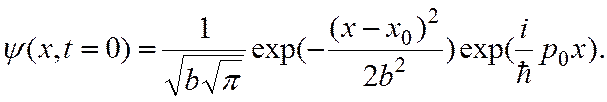


 ) в рамках задачи о свободном движении частицы. В квантовой механике роль начального условия играет задание волновой функции системы в момент t = 0. Подберем эту волновую функцию таким образом, чтобы при t = 0 средние значения координаты и импульса свободной частицы равнялись заданным значениям
) в рамках задачи о свободном движении частицы. В квантовой механике роль начального условия играет задание волновой функции системы в момент t = 0. Подберем эту волновую функцию таким образом, чтобы при t = 0 средние значения координаты и импульса свободной частицы равнялись заданным значениям 




 .
. можно доказать (3) и вычислить средние величины, входящие в (1) и (2) и из (1), (2) вычислить дисперсии координаты и импульса:
можно доказать (3) и вычислить средние величины, входящие в (1) и (2) и из (1), (2) вычислить дисперсии координаты и импульса:


 .
.





 . В результате получим:
. В результате получим:
 знаменатели в (7) обращаются в
знаменатели в (7) обращаются в  и (7) теряет смысл. Следовательно, функция
и (7) теряет смысл. Следовательно, функция  должна содержать в качестве сомножителя синус:
должна содержать в качестве сомножителя синус:

 в знаменателе (9) (причину этого смотри выше) полагаем
в знаменателе (9) (причину этого смотри выше) полагаем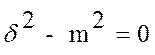 , откуда следует:
, откуда следует:
 .
.

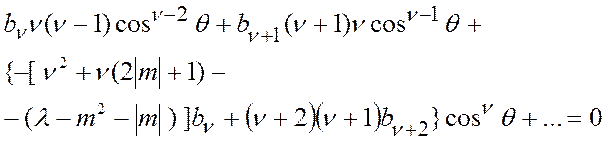
 равны нулю. Приравнивая к нулю эти коэффициенты, получаем:
равны нулю. Приравнивая к нулю эти коэффициенты, получаем:


 через предыдущий
через предыдущий  . Из (16) следует, что ряд (12) может содержать либо четные степени косинусов
. Из (16) следует, что ряд (12) может содержать либо четные степени косинусов  , либо нечетные
, либо нечетные  . В общем виде (12) принимает вид:
. В общем виде (12) принимает вид:



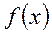 заменить на f (0). Вынося это постоянное число за знак интеграла и пользуясь последним условием (2), мы получим (3).
заменить на f (0). Вынося это постоянное число за знак интеграла и пользуясь последним условием (2), мы получим (3).
 входящего в состав функции
входящего в состав функции  атома водорода и записать окончательный вид этой функции. Установить величину орбитального механического момента импульса М и возможные значения механического орбитального квантового числа l электрона в атоме водорода.
атома водорода и записать окончательный вид этой функции. Установить величину орбитального механического момента импульса М и возможные значения механического орбитального квантового числа l электрона в атоме водорода.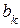 - последний ненулевой коэффициент полинома (17). Тогда, учитывая, что
- последний ненулевой коэффициент полинома (17). Тогда, учитывая, что 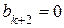 , из (16) получаем:
, из (16) получаем:
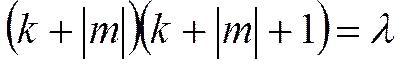



 , то
, то  , т.е.
, т.е. 
 , или
, или  , или
, или





 полинома устанавливаются через предыдущие коэффициенты
полинома устанавливаются через предыдущие коэффициенты  с помощью рекуррентной формулы
с помощью рекуррентной формулы
 будет в конечном итоге играть роль нормировочного коэффициента и определяться из условия нормировки. Однако, можно упростить получение полинома в (1) и вместо поиска нормировочных коэффициентов для
будет в конечном итоге играть роль нормировочного коэффициента и определяться из условия нормировки. Однако, можно упростить получение полинома в (1) и вместо поиска нормировочных коэффициентов для  установить формулу для общего нормировочного коэффициента. Для этого коэффициент
установить формулу для общего нормировочного коэффициента. Для этого коэффициент  представляют в виде:
представляют в виде:
 получается полином
получается полином  вида:
вида:
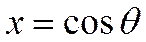 . Сферическая функция (1) при этом принимает вид:
. Сферическая функция (1) при этом принимает вид:
 устанавливается из условия нормировки
устанавливается из условия нормировки

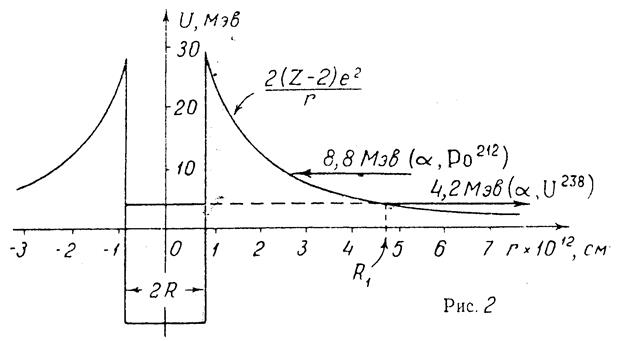
 показана на рисунке 2. При r < R (R – радиус действия на α - частицу ядерных сил, величина которого близка к радиусу ядра) ход потенциальной
показана на рисунке 2. При r < R (R – радиус действия на α - частицу ядерных сил, величина которого близка к радиусу ядра) ход потенциальной
 - заряд дочернего ядра, электрическое поле которого отталкивает α – частицу, обладающую энергией 2 e.
- заряд дочернего ядра, электрическое поле которого отталкивает α – частицу, обладающую энергией 2 e.



 (см.7б-2), а
(см.7б-2), а  (см.7в-21), подставим (3) в (2) и перенесем все в левую часть и сгруппируем слагаемые. В результате (2) примет вид:
(см.7в-21), подставим (3) в (2) и перенесем все в левую часть и сгруппируем слагаемые. В результате (2) примет вид: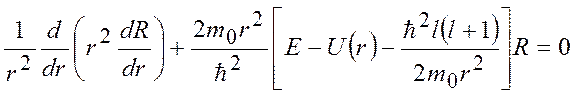

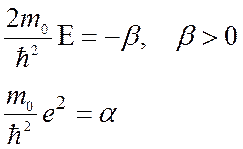
 в (5), последнее приобретает вид:
в (5), последнее приобретает вид:

 -асимптотическая функция, отыскиваемая при условии
-асимптотическая функция, отыскиваемая при условии  , т.е. в области, где
, т.е. в области, где  . Подставляя (8) в (7) получаем:
. Подставляя (8) в (7) получаем: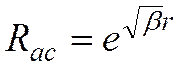
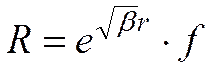
 отыскивается в виде ряда по степеням r, аналогично методу определения сферических функций
отыскивается в виде ряда по степеням r, аналогично методу определения сферических функций  (см.7в1-8). В результате из (7) устанавливается полная функция
(см.7в1-8). В результате из (7) устанавливается полная функция  :
:
 ,
,  – радиус первой боровской орбиты,
– радиус первой боровской орбиты,  - главное квантовое число. Коэффициенты
- главное квантовое число. Коэффициенты  определяются через рекуррентную формулу:
определяются через рекуррентную формулу: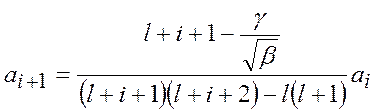
 ,
,  . Последнее выражение и явный вид
. Последнее выражение и явный вид 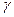 и
и 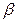 (см. (6)) позволяют установить формулу полной энергии атома водорода:
(см. (6)) позволяют установить формулу полной энергии атома водорода: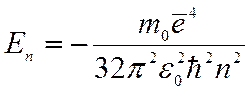


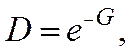 где
где 
 Тогда вычисления приводят к следующему выражению для G:
Тогда вычисления приводят к следующему выражению для G:





