
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дельта-функция Дирака, ее свойства и интерпретация в физике.Стр 1 из 3Следующая ⇒
БИЛЕТ № 2 1). Нормировка в ящике волновой функции свободной частицы. Как известно собственные функции оператора Гамильтона свободной частицы имеют вид
где С - число, Эти функции квадратично не интегрируемы, т.е. интеграл от квадрата их модуля по бесконечности расходится (равен бесконечности). Вследствие расходимости этого интеграла обычный способ нормировки на единицу неприменим и для отыскания числового коэффициента С в (3) пользуются несколькими методами, одним из которых получил название «нормировка в ящике». В рамках этого метода ограничиваются заданием функции (3) в произвольно большом, но конечном кубе объема
Тогда условие нормировки для одномерного движения, например вдоль оси х принимает вид:
Подставляя
Используя условие периодичности (4) можно показать, что вектор
где квантовые числа
Выбирая Интересно отметить, что собственными функциями (6) нельзя пользоваться внутри ящика с идеально твердыми стенками, т.к. эти функции нигде не обращаются в нуль. Это аналогично классической ситуации, когда импульс частицы не сохраняется при отражении от твердочй стенки. С другой стороны, кубический ящик, на стенках которого волновая функция должна подчиняться граничным условиям периодичности, соответствует случаю, когда все бесконечное пространство разделено на кубы, и все волновые функции периодичны с периодом
Легко убедиться в том, что собственные функции (6) оператора полной энергии ортонормированны. Действительно, интегрируя по области объема
где δ- символ Кронекера: Смотри 2 вопрос билета №1
3). Билет №3. 1)
Смотри 2 вопрос билета №1 Билет №4. Смотри 2 вопрос билета №1
3).
Билет № 5. 1). Аналитическое представление δ -функции Дирака.Нормировка на δ-функцию. Аналитическое представление δ-функции Дирака. Как известно, δ -функцией Дирака называют функцию δ (β), удовлетворяющую следующим условиям:
Из (1) следует, что функция δ (β) носит резко выраженный сингулярный характер. Качественно ее можно представить себе равной нулю всюду, кроме точки β = 0, а в этой точке настолько большой, что площадь, ограниченная графиком этой функции и осью β, конечна и равна единице. Весьма полезным оказывается одно частное представление δ (β) в виде предельного значения функции
Нормировка на δ-функцию Дирака. Представлением δ – функции в виде (2) можно воспользоваться при нормировке собственной функции оператора Гамильтона свободной частицы. Как известно, эта функция имеет вид
где С - число, Эта функция квадратично не интегрируема, т.е. интеграл от квадрата модуля этой функции по бесконечности расходится (равен бесконечности). Вследствие расходимости этого интеграла обычный способ нормировки на единицу неприменим. Будем искать нормировочный коэффициент С, который бы во первых, отвечал свойству ортогональности волновых функций (3), а во вторых соответствовал бы расходимости указанного выше интеграла. Рассмотрим одномерный случай движения вдоль оси x. Пусть
Рассчитаем интеграл ортогональности собственных функций (3) для этого движения с учетом (1) и (2):
Если в (5)
т.е. при Таким образом
Аналогичные вычисления можно сделать и для оставшихся координат y и z. Тогда из (3) следует, что
А общее условие ортогональности есть
Смотри 2 вопрос билета №1
3).
Билет №7 Понятие дисперсии координаты и импульса. Минимизирующий волновой пакет свободной частицы. Дисперсия и средние значения координаты и импульса в начальный момент времени для минимизирующего волнового пакета
Как известно, понятие дисперсии сводится к понятию среднеквадратичного отклонения рассматриваемой величины от его среднего значения. В частности, дисперсия координаты задается выражением
а дисперсия импульса -
Рассмотрим эти понятия (
а неопределенности координаты и импульса были бы минимальными, т.е.
Можно показать, что этим требованиям отвечает функция
Она нормирована в соответствии с общим правилом нормировки
И нормировочный коэффициент равен величине Пользуясь определением среднего в квантовой механике
Из (7) следует
Отсюда видно, что выбранная волновая функция (5) обладает уникальным свойством – она минимизирует соотношение неопределенностей Гейзенберга, приводя к равенству (4), т.к. (8) тождественно (4). Из (7) видно, что квадрат величины b, входящей в нормировочный коэффициент волновой функции (5) имеет смысл удвоенной дисперсии координаты свободной частицы в начальный момент времени. Можно показать, что состояние с волновой функцией (5) не является стационарным и энергия не имеет определенного значения. Такое нестационарное состояние частицы, довольно четко локализованное в пространстве, является примером пространственного волнового пакета.
Пояснить графики
3).
Билет №8 1) Эволюция во времени средних значений координаты, импульса и их дисперсии минимизирующего волнового пакета Считать вид пакета в начальный и произвольный момент времени известными:
Чтобы выяснить, как ведет себя с течением времени свободная частица, которая в начальный момент находится в состоянии с волновой функцией
необходимо решить общее уравнение Шредингера. Это решение имеет вид:
Пользуясь определением среднего в квантовой механике
Из (3) видно, что «в среднем» свободная квантовая частица движется также, как классическая, начинающая движение из точки
Она оказывается равной
Из (5) видно, что
т.е. волновой пакет (2), описывающий состояние свободного движения частицы, «расплывается» с течением времени. Скорость этого расплывания можно характеризовать временем
Из (7) видно, что чем меньше первоначальная неопределенность координаты ( Дисперсия импульса в состоянии (2), вычисленная по формуле
оказывается равной
Она, как и Если область первоначальной локализации частицы очень велика
2). Пояснить формулы:
Стационарное уравнение Шредингера для атома водорода разделяется на два уравнения: 1) сферическое:
2) радиальное:
Уравнение (1) хорошо известно в математике (см. любой курс методов математической физики, раздел «Уравнение Лапласа в сферических координатах»). Искомые решения
где
Нормировочный множитель в формуле (3) определяется из условия нормировки:
Из уравнения (2) устанавливается явный вид радиальных функций:
где Коэффициенты
где Кроме того, из (2) следует:
Решение уравнения (1) приводит к количественным результатам:
Выше приведены следующие обозначения для физических величин, описывающих состояние электрона в атоме водорода: 3). Билет №9 1)
Прохождением частиц через потенциальные барьеры объясняется целый ряд физических явлений: внешняя контактная разность потенциалов при соприкосновении разнородных проводников, холодная эмиссия электронов (испускание электронов с поверхности проводнка при напряженности электрического поля вблизи этой поверхности свыше ~ 100 кэВ/см), некоторые ососбенности ядерных реакций (например попадание протона внутрь ядра извне при его кинетической энергии, меньшей чем энергия электрического отталкивания ядра атома), спонтанный α – распад радиоактивных ядер и др.
2) Дать названия элементам, входящие в формулы:
Деление переменных в стационарном уравнении Шредингера для атома водорода
заданном в сферической системе координат, приводит к разделению (1) на три уравнения, каждое из которых зависит от своей переменной. Уравнение, зависящее от радиуса r, называется радиальным уравнением и имеет вид:
где
Учтем, что
Беря производные в (4) и проводя преобразования, получаем:
Введем обозначения:
После подстановки (6) и
Решение уравнения (7) отыскивается в виде произведения двух функций
где
Тогда
Функция
где
где
3)
Билет №10 1)Энергетический спектр спонтанного α-распада атомных ядер. Квантовомеханическое толкование спонтанной α- радиоактивности. Ядра одного и того же изотопа могут испускать α-частицы с несколькими строго определенными значениями энергии. Иначе говоря, α-частицы обладают дискретным энергетическим спектром. На рисунке 1 показана схема распада ядер изотопа урана
Конечным продуктом распада в этом случае является изотоп тория Таким образом, если при Рассмотрим коротко теорию α-распада. По современным представлениям α-частиц в ядре постоянно не существует. Они образуются при встрече движущихся внутри ядра двух протонов и двух нейтронов, а затем, спустя достаточно короткое время, распадаются на составные части. На образовавшуюся α-частицу, когда она находится внутри ядра, со стороны остальных нуклонов действуют ядерные силы притяжения и со стороны протонов – силы электрического отталкивания. Действия ядерных сил при этом значительно больше электрического отталкивания, иначе α-частица не смогла бы оставаться в ядре и вылетела бы из него после образования через промежуток времени порядка 2) Разложение δ – функции в ряд Фурье. Фурье – образ δ – функции. Известно, что любую функцию f (х), обладающую достаточно хорошим поведением, можно разложить в интеграл Фурье
где фурье-образ
Оказывается, что в интеграл Фурье можно разложить и δ-функцию:
откуда видно, что ее фурье-образ равен просто числу:
Поэтому, с точки зрения теории интеграла Фурье δ-функция является в некотором смысле наиболее простой функцией. Совершенно формально в справедливости (8), а тем самым и разложения (7), можно убедиться, подставляя в (6) f (х)=δ(х) и используя основное свойство δ-функции (3). Однако с математической точки зрения этот аргумент ни в коей мере нельзя рассматривать как доказательство, которое в действительности является весьма сложным и приводится в курсах теории обобщенных функций.
3)
Билет №11 1) Применение модели потенциальной ямы к описанию состояния α-частицы внутри α - радиоактивного ядра
Здесь Z – порядковый номер материнского ядра, а При самопроизвольном распаде ядра α – частица не получает энергии извне. Поэтому ее энергия с при любых значениях r как внутри, так и вне ядра должна быть постоянной (для ядра урана 2). Для δ – функции Дирака закончить равенства: 1) Ответы 1)1 2)
3).
Билет №12 1)Применение модели потенциальной ямы для установления формулы связи постоянной радиоактивного распада λ, свойствами ядра и энергией α- частицы в явлении спонтанной α- радиоактивности атомных ядер. Энергия α - частиц, возникающих при распаде ядер, лежит обычно в пределах от 4 до 8 Мэв, (максимум 10,5 Мэв, минимум 1,8 Мэв). При этом имеется тенденция к уменьшению периода полураспада с увеличением энергии α- частиц. Особенно эта тенденция проявляется при последовательных радиоактивных превращениях в пределах одного и того же радиоактивного семейства (закон Гейгера - Нэттола). Например, энергия α - частиц при распаде урана Теоретическое обоснование этой закономерности можно пояснить следующим образом. Воспользуемся теорией прохождения частиц через потенциальный барьер и установим связь между постоянной распада λ, свойствами ядра и энергией α – частицы. Предположим для простоты, что α – частица существует в ядре постоянно и движется по радиксу внутри потенциальной ямы, образованной ядерными силами, «ударяясь о стенки этой ямы». Вероятность пройти через потенциальный барьер в единицу времени и оказаться вне ядра для этой частицы должна быть, с одной стороны, пропорциональна числу «попыток», которые предпринимает частица в единицу времени, чтобы выйти из ядра, т.е. числу соударений
За единицу времени α – частица проходит внутри ядра путь, численно равный ее скорости. За это время она испытает столько столкновений со стенками потенциальной ямы, сколько раз в этом пути укладывается диаметр ямы 2R. Следовательно,
годе
Таким образом, число соударений α – частицы со стенками потенциальной ямы в единицу времени равно
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 802; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.93.209 (0.133 с.) |
 или
или 
 - волновой вектор свободно движущейся частицы с импульсом
- волновой вектор свободно движущейся частицы с импульсом  , а компоненты вектора
, а компоненты вектора  с центром в начале координат. На стенках этого куба функции (3) должны удовлетворять граничным условиям периодичности
с центром в начале координат. На стенках этого куба функции (3) должны удовлетворять граничным условиям периодичности

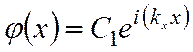 в (5) получаем
в (5) получаем  . Аналогичные расчеты для двух других осей приводят к тем же результатам. Тогда для полной функции (3) имеем
. Аналогичные расчеты для двух других осей приводят к тем же результатам. Тогда для полной функции (3) имеем  и окончательно
и окончательно или
или 

 положительные или отрицательные целые числа или нули. Соответственно собственные значения оператора полной энергии равны
положительные или отрицательные целые числа или нули. Соответственно собственные значения оператора полной энергии равны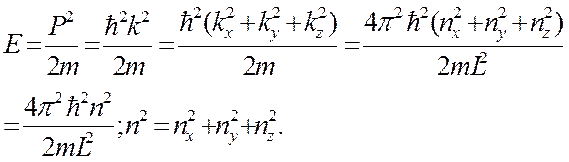
 достаточно большим, можно делать расстояния между соседними собственными векторами
достаточно большим, можно делать расстояния между соседними собственными векторами  , получаем
, получаем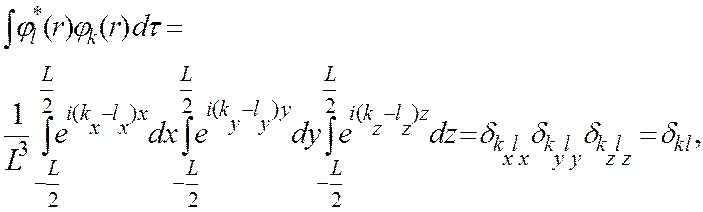
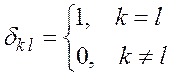 , где первое условие отвечает условию нормировки, а второе – ортогональности волновых функций.
, где первое условие отвечает условию нормировки, а второе – ортогональности волновых функций.



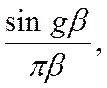 где g – положительное вещественное число. Эта функция, равная
где g – положительное вещественное число. Эта функция, равная  при β = 0 при увеличении
при β = 0 при увеличении 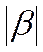 осциллирует с постоянно убывающей амплитудой и с периодом
осциллирует с постоянно убывающей амплитудой и с периодом  а интеграл от нее по β, взятый в пределах
а интеграл от нее по β, взятый в пределах  равен единице независимо от значения g. Поэтому предел
равен единице независимо от значения g. Поэтому предел  при
при  имеет все свойства δ - функции; при β = 0 он становится бесконечно большим, интеграл от предельного выражения равен единице, а бесконечно быстрые осцилляции при увеличении
имеет все свойства δ - функции; при β = 0 он становится бесконечно большим, интеграл от предельного выражения равен единице, а бесконечно быстрые осцилляции при увеличении  означают, что весь вклад в интеграл, содержащий эту функцию, обусловлен бесконечно малой окрестностью точки β = 0. В связи с этим можно положить
означают, что весь вклад в интеграл, содержащий эту функцию, обусловлен бесконечно малой окрестностью точки β = 0. В связи с этим можно положить

 , а компоненты вектора
, а компоненты вектора 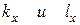 - компоненты вектора
- компоненты вектора 
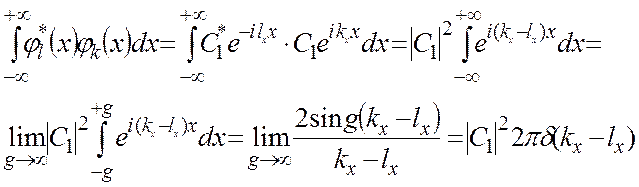
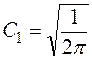 , то интеграл
, то интеграл 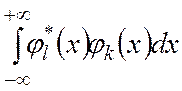 становится равным δ -функции Дирака и, следовательно обладает его свойствами (1):
становится равным δ -функции Дирака и, следовательно обладает его свойствами (1):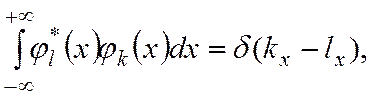
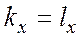 интеграл в (6) равен
интеграл в (6) равен 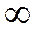 , а при
, а при 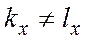 - обращается в ноль. Последнее соответствует свойству ортогональности рассматриваемых функций.
- обращается в ноль. Последнее соответствует свойству ортогональности рассматриваемых функций.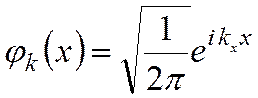
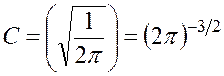 и для бесконечного пространства собственные функции оператора Гамильтона свободной частицы приобретают вид:
и для бесконечного пространства собственные функции оператора Гамильтона свободной частицы приобретают вид: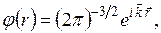


 свободной частицы:
свободной частицы:


 ) в рамках задачи о свободном движении частицы. В квантовой механике роль начального условия играет задание волновой функции системы в момент t = 0. Подберем эту волновую функцию таким образом, чтобы при t = 0 средние значения координаты и импульса свободной частицы равнялись заданным значениям
) в рамках задачи о свободном движении частицы. В квантовой механике роль начального условия играет задание волновой функции системы в момент t = 0. Подберем эту волновую функцию таким образом, чтобы при t = 0 средние значения координаты и импульса свободной частицы равнялись заданным значениям 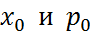




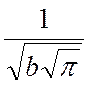 .
. можно доказать (3) и вычислить средние величины, входящие в (1) и (2) и из (1), (2) вычислить дисперсии координаты и импульса:
можно доказать (3) и вычислить средние величины, входящие в (1) и (2) и из (1), (2) вычислить дисперсии координаты и импульса:

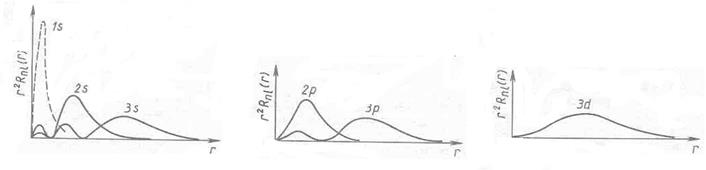




 свободной частицы, плотность его координатного распределения и скорость расплывания.
свободной частицы, плотность его координатного распределения и скорость расплывания.

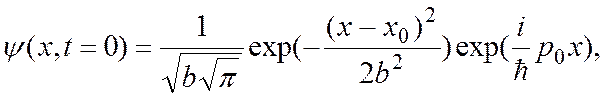


 с импульсом
с импульсом  Однако в квантовом случае в заданный момент t координата частицы не имеет определенного значения: она «размазана» вокруг точки
Однако в квантовом случае в заданный момент t координата частицы не имеет определенного значения: она «размазана» вокруг точки  с дисперсией
с дисперсией 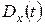 , которую можно найти из (2), пользуясь определением дисперсии:
, которую можно найти из (2), пользуясь определением дисперсии: .
.

 с течением времени увеличивается. При этом из (2) можно вычислить плотность координатного распределения
с течением времени увеличивается. При этом из (2) можно вычислить плотность координатного распределения  :
:
 , в течении которого первоначальная (при
, в течении которого первоначальная (при  ) дисперсия координаты
) дисперсия координаты  удваивается:
удваивается:
 ), тем быстрее происходит расплывание пакета. Это явление не имеет аналога в классической механике, поскольку размеры области локализации классической корпускулы в данный момент времени полностью определяются ее собственными размерами и не зависят от времени.
), тем быстрее происходит расплывание пакета. Это явление не имеет аналога в классической механике, поскольку размеры области локализации классической корпускулы в данный момент времени полностью определяются ее собственными размерами и не зависят от времени.

 , не зависит от времени, что и должно быть для интеграла движения.
, не зависит от времени, что и должно быть для интеграла движения. , расплывание пакета происходит настолько медленно, что в течение большого промежутка времени не происходит заметного изменения дисперсии
, расплывание пакета происходит настолько медленно, что в течение большого промежутка времени не происходит заметного изменения дисперсии  , причем
, причем  . Следовательно, в этом случае свободное движение частицы очень похоже на распространение монохроматической плоской волны. Увеличивая b, можно сколько угодно приближаться к состоянию плоской волны, однако состояние с
. Следовательно, в этом случае свободное движение частицы очень похоже на распространение монохроматической плоской волны. Увеличивая b, можно сколько угодно приближаться к состоянию плоской волны, однако состояние с  не может быть реализовано никогда. Следует отметить, что дисперсия координаты
не может быть реализовано никогда. Следует отметить, что дисперсия координаты 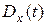 согласно (5) не зависит от среднего импульса частицы
согласно (5) не зависит от среднего импульса частицы  . Поэтому рассмотренная картина расплывания пакета имеет место и в том случае, когда частица в среднем покоится
. Поэтому рассмотренная картина расплывания пакета имеет место и в том случае, когда частица в среднем покоится  .
.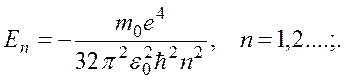

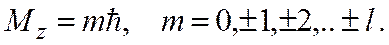

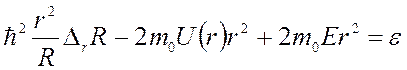
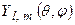 уравнения (1) называются сферическими функциями. Они зависят от целых чисел l и m, что отражено в их символическом обозначении. Эти функции имеют явный вид:
уравнения (1) называются сферическими функциями. Они зависят от целых чисел l и m, что отражено в их символическом обозначении. Эти функции имеют явный вид:
 - присоединенный полином Лежандра от аргумента cos θ вычисляется по формуле:
- присоединенный полином Лежандра от аргумента cos θ вычисляется по формуле:
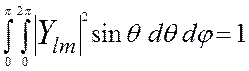

 , r 1- радиус первой Боровской орбиты, i = 0,1,2,...
, r 1- радиус первой Боровской орбиты, i = 0,1,2,...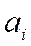 вычисляются из рекуррентной формулы, полученной из решения радиального уравнения (2):
вычисляются из рекуррентной формулы, полученной из решения радиального уравнения (2):
 ,
, 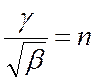 .
.
 ,
,

 - полная энергия,
- полная энергия, 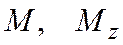 - орбитальный механический момент импульса и его проекция на ось z соответственно, n - главное квантовое число,
- орбитальный механический момент импульса и его проекция на ось z соответственно, n - главное квантовое число, 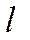 - механическое орбитальное квантовое число, m – магнитное орбитальное квантовое число.
- механическое орбитальное квантовое число, m – магнитное орбитальное квантовое число.

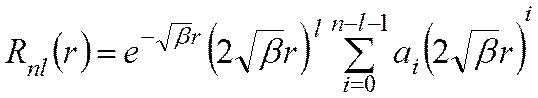

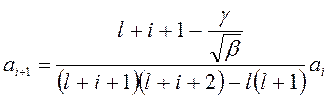


 .
.
 (см.7б-2), а
(см.7б-2), а  (см.7в-21), подставим (3) в (2) и перенесем все в левую часть и сгруппируем слагаемые. В результате (2) примет вид:
(см.7в-21), подставим (3) в (2) и перенесем все в левую часть и сгруппируем слагаемые. В результате (2) примет вид:

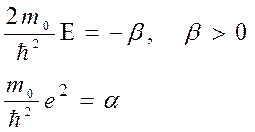
 в (5), последнее приобретает вид:
в (5), последнее приобретает вид:

 -асимптотическая функция, отыскиваемая при условии
-асимптотическая функция, отыскиваемая при условии 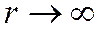 , т.е. в области, где
, т.е. в области, где  . Подставляя (8) в (7) получаем:
. Подставляя (8) в (7) получаем: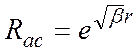
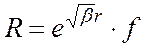
 отыскивается в виде ряда по степеням r, аналогично методу определения сферических функций
отыскивается в виде ряда по степеням r, аналогично методу определения сферических функций  (см.7в1-8). В результате из (7) устанавливается полная функция
(см.7в1-8). В результате из (7) устанавливается полная функция  :
: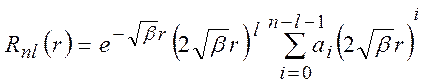
 ,
, 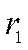 – радиус первой боровской орбиты,
– радиус первой боровской орбиты,  - главное квантовое число. Коэффициенты
- главное квантовое число. Коэффициенты  определяются через рекуррентную формулу:
определяются через рекуррентную формулу:
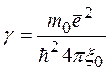 ,
,  . Последнее выражение и явный вид
. Последнее выражение и явный вид  и
и  (см. (6)) позволяют установить формулу полной энергии атома водорода:
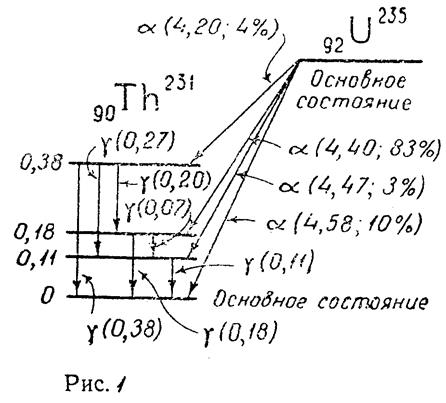
(см. (6)) позволяют установить формулу полной энергии атома водорода:

 .
.
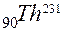 . Около уровней ядра
. Около уровней ядра  -распаде дочернее ядро получается сразу в основном состоянии, то α-частица при этом испускается с наибольшей возможной энергией. Если же дочернее ядро получается в одном из возбужденных состояний, то энергия α-частицы оказывается меньше, но дочернее ядро испускает затем γ-кванты. Сумма энергий γ-квантов, испущенных в этом случае, и энергии α-частицы должна быть, конечно, равна наибольшей энергии, которую может иметь α-частица, испускаемая данным материнским ядром.
-распаде дочернее ядро получается сразу в основном состоянии, то α-частица при этом испускается с наибольшей возможной энергией. Если же дочернее ядро получается в одном из возбужденных состояний, то энергия α-частицы оказывается меньше, но дочернее ядро испускает затем γ-кванты. Сумма энергий γ-квантов, испущенных в этом случае, и энергии α-частицы должна быть, конечно, равна наибольшей энергии, которую может иметь α-частица, испускаемая данным материнским ядром. (время, в течение которого α-частица проходит ядро от одного края до другого), т.е. материнское ядро не смогло бы существовать сколько-нибудь продолжительное время. Если же α-частица оказывается вне ядра за границей действия ядерных сил, то на нее действуют лишь силы электрического отталкивания. Эти силы и сообщают α-частицам ту энергию, которая наблюдается у них при α-распаде.
(время, в течение которого α-частица проходит ядро от одного края до другого), т.е. материнское ядро не смогло бы существовать сколько-нибудь продолжительное время. Если же α-частица оказывается вне ядра за границей действия ядерных сил, то на нее действуют лишь силы электрического отталкивания. Эти силы и сообщают α-частицам ту энергию, которая наблюдается у них при α-распаде. ,
,
 этой функции равен
этой функции равен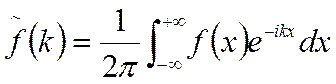
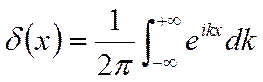


 Зависимость потенциальной энергии U(r) α - частицы от ее расстояния r до центра ядра
Зависимость потенциальной энергии U(r) α - частицы от ее расстояния r до центра ядра  показана на рисунке 2. При r < R (R – радиус действия на α - частицу ядерных сил, величина которого близка к радиусу ядра) ход потенциальной энергии приближенно представлен в виде потенциальной ямы с вертикальными стенками. При r > R, когда на α - частицу действуют только силы электрического отталкивания, ход потенциальной энергии определяется формулой для энергии взаимодействия двух точечных электрических зарядов:
показана на рисунке 2. При r < R (R – радиус действия на α - частицу ядерных сил, величина которого близка к радиусу ядра) ход потенциальной энергии приближенно представлен в виде потенциальной ямы с вертикальными стенками. При r > R, когда на α - частицу действуют только силы электрического отталкивания, ход потенциальной энергии определяется формулой для энергии взаимодействия двух точечных электрических зарядов:
 - заряд дочернего ядра, электрическое поле которого отталкивает α – частицу, обладающую энергией 2e. Таким образом, потенциальная энергия α – частицы имеет вид барьера, расположенного вокруг ядра, наибольшая высота которого для изотопа урана
- заряд дочернего ядра, электрическое поле которого отталкивает α – частицу, обладающую энергией 2e. Таким образом, потенциальная энергия α – частицы имеет вид барьера, расположенного вокруг ядра, наибольшая высота которого для изотопа урана  составляет около 28 Мэв, если радиус области, внутри которой на α – частицу действуют ядерные силы, вычислять по формуле
составляет около 28 Мэв, если радиус области, внутри которой на α – частицу действуют ядерные силы, вычислять по формуле  (однако этот радиус несколько больше радиуса ядра, поскольку действие ядерных сил простирается на небольшое расстояние за границы области, где расположены нуклоны). Наличие такого барьера подтверждается опытами по рассеиванию α – частиц на ядрах тяжелых элементов. Согласно этим опытам α – частицы, испускаемые радиоактивными элементами (например, α – частицы с энергией 8,8 Мэв, испускаемые ядрами изотопа полония
(однако этот радиус несколько больше радиуса ядра, поскольку действие ядерных сил простирается на небольшое расстояние за границы области, где расположены нуклоны). Наличие такого барьера подтверждается опытами по рассеиванию α – частиц на ядрах тяжелых элементов. Согласно этим опытам α – частицы, испускаемые радиоактивными элементами (например, α – частицы с энергией 8,8 Мэв, испускаемые ядрами изотопа полония  ), испытывают на ядрах резерфордовское рассеяние, т.е. силы, действующие на α – частицы со стороны ядер, когда они подходят к ядрам снаружи, описываются законом Кулона.
), испытывают на ядрах резерфордовское рассеяние, т.е. силы, действующие на α – частицы со стороны ядер, когда они подходят к ядрам снаружи, описываются законом Кулона.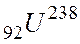 Е = 4,2 Мэв). Чтобы выйти из ядра α – частица должна пройти область значений r от R до R1, в которой ее потенциальная энергия больше полной и в которой она согласно законам классической механики не может находиться без нарушения закона сохранения энергии. Следовательно, с точки зрения классической механики α – распад объяснить нельзя. Объяснение α - распад получил в квантовой механике, согласно которой имеется некоторая вероятность, что частица пройдет через потенциальный барьер, несмотря на то, что энергии частицы для этого не хватает (это явление, как известно, носит название туннельного эффекта).
Е = 4,2 Мэв). Чтобы выйти из ядра α – частица должна пройти область значений r от R до R1, в которой ее потенциальная энергия больше полной и в которой она согласно законам классической механики не может находиться без нарушения закона сохранения энергии. Следовательно, с точки зрения классической механики α – распад объяснить нельзя. Объяснение α - распад получил в квантовой механике, согласно которой имеется некоторая вероятность, что частица пройдет через потенциальный барьер, несмотря на то, что энергии частицы для этого не хватает (это явление, как известно, носит название туннельного эффекта).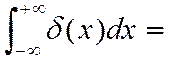 2)
2)  3)
3) 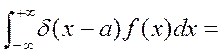 4)
4)  5)
5) 
 3)
3)  4)
4)  5)
5) 

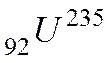
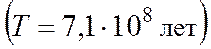 составляет 4, 58 Мэв, при распаде протактиния
составляет 4, 58 Мэв, при распаде протактиния 
 - 5,04 Мэв и при распаде полония
- 5,04 Мэв и при распаде полония 
 - 7,36 Мэв (приведены α- частицы с наибольшими энергиями).
- 7,36 Мэв (приведены α- частицы с наибольшими энергиями). частицы со стенками ямы за это время. С другой стороны, она пропорциональна коэффициенту D прохождения через барьер, который показывает, какая доля из этих «попыток» может увенчаться успехом. Вероятность появления α - частицы вне ядра и есть вероятность распада. Вероятность же распада в единицу времени равна постоянной распада λ. Таким образом
частицы со стенками ямы за это время. С другой стороны, она пропорциональна коэффициенту D прохождения через барьер, который показывает, какая доля из этих «попыток» может увенчаться успехом. Вероятность появления α - частицы вне ядра и есть вероятность распада. Вероятность же распада в единицу времени равна постоянной распада λ. Таким образом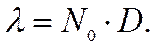

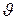 -скорость α – частицы внутри ямы. Чтобы найти
-скорость α – частицы внутри ямы. Чтобы найти  , обратимся к формуле для энергии первого уровня в одномерной потенциальной яме шириной b:
, обратимся к формуле для энергии первого уровня в одномерной потенциальной яме шириной b: 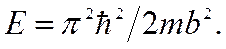 Эта формула выведена из предположения, что энергия частицы отсчитывается от дна ямы. В этом случае полная энергия равна кинетической, т.е.
Эта формула выведена из предположения, что энергия частицы отсчитывается от дна ямы. В этом случае полная энергия равна кинетической, т.е.  Можно показать, что для сферически симметричной потенциальной ямы b следует заменить на R. Тогда
Можно показать, что для сферически симметричной потенциальной ямы b следует заменить на R. Тогда  (m – масса α – частицы). Отсюда
(m – масса α – частицы). Отсюда



