
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зная уровень напряжения, можно рассчитать уровни токаСтр 1 из 6Следующая ⇒
Краткие сведения из теории В процессе изучения основных свойств пассивных электрических цепей, широко применяемых в устройствах железнодорожной телемеханики и связи, наиболее часто приходится выполнять измерения уровней электрических величин и комплексных сопротивлений. Понятие уровня вводится для сужения пределов нормируемых величин из-за того, что при передаче электрических сигналов имеют место большое разнообразие и изменение мощности, напряжения и тока. Уровнем какой-либо величины называется ее логарифмическая мера. Если при определении уровня вычисляется десятичный логарифм отношения исследуемых величин, то он выражается в белах, если натуральный – в неперах. Широко используется при измерениях десятая доля бела – децибел. Имеются три разновидности уровней передачи электрических величин: абсолютные, относительные и измерительные. Абсолютным уровнем называется логарифмическая мера отношения исследуемой величины к величине того же рода, условно принятой за единицу. При измерении исследуемых величин наиболее часто используются уровни напряжения, мощности и тока. Если для определения уровней передачи за единицу приняты величины полной мощности S0 = 1 мВ×А, напряжения U0 = 0,775 В и тока I0 = 1,29 мА при сопротивлении R0 = 600 Ом, то полученные при этом уровни будут абсолютными. Относительным уровнем называется логарифмическая мера отношения исследуемой величины к величине того же рода, взятой в произвольной точке цепи. Измерительным называется абсолютный уровень в рассматриваемой точке цепи, когда к началу ее подведено напряжение с уровнем «0 дБ». Значение абсолютного уровня напряжения может быть измерено специальным прибором – указателем уровня, представляющим собой вольтметр, шкала которого проградуирована в логарифмических единицах, или вычислено по формулам:
Рис. 1.1. Схемы измерения сопротивлений Рис. 1.2. Схема измерения полного сопротивления Методом двух вольтметров
Далее добавочное сопротивление заменяют другим ( Если ввести условные обозначения
то
При использовании в качестве добавочных сопротивлений резисторов R1 и R2 в формуле (1.10) значение коэффициента
Для повышения точности измерений необходимо принять: 1) значение коэффициента р – в пределах от 5 до 20; 2) значения добавочных сопротивлений Z1 и Z2 - соизмеримыми с Zх; 3) отсчет Vх и V0 выполнять по одному и тому же прибору без переключения шкалы. Порядок выполнения работы 1.2.1. Измерить уровень напряжения на различных сопротивлениях нагрузки. 1.2.2. Измерить комплексное сопротивление индуктивного и емкостного характера (частота генератора и параметры цепи задаются преподавателем) методом двух вольтметров. 1.2.3. Изучить порядок и выполнить измерение сопротивлений с помощью уравновешенного моста, используя программный продукт «Лабораторные работы по ТЛЭЦ». 1.2.4. Собрать аналогичную схему, используя программный продукт Workbench, выполнить измерения. 1.2.5. Обработать экспериментальные данные, результаты измерений проанализировать. 1.2.6. Ответить на контрольные вопросы. Содержание отчета
1) Титульный лист с указанием дисциплины, кафедры, наименования работы, номера группы, фамилии и инициалов студента, а также даты выполнения работы. 2) Цель работы. 3) Схемы измерений и расчетные формулы с пояснениями. 4) Таблицы измерений и вычислений. 5) Графики, выполненные на миллиметровой бумаге. 6) Подробные образцы теоретических расчетов и обработки экспериментальных данных (контрольные примеры). 7) Подписанный преподавателем черновик, содержащий результаты измерений. 8) Ответы на контрольные вопросы. Отчет должен быть оформлен аккуратно. Сокращения слов, кроме общепринятых, не допускаются. Отчет может быть выполнен с использованием ПЭВМ (формат А4) или написан вручную на тетрадных листах с учетом всех требований стандарта СТП ОмГУПС-3.1-02.
1.6. Контрольные вопросы
1) Что такое абсолютный, относительный и измерительный уровни напряжения, тока, мощности? 2) Как, зная абсолютный (относительный) уровень сигнала, определить напряжение, ток, мощность? 3) Установить соотношение между неперами и децибелами.
4) Как выбрать оптимальное значение нагрузки? 5) Как определить, уравновешен ли мост? 6) Почему в режиме «Инд.» не удается сбалансировать мост, если сопротивление Rэ = 0?
Лабораторная работа 2 ИССЛЕДОВАНИЕ РЕАКТИВНОГО ДВУХПОЛЮСНИКА
Ц е л ь р а б о т ы - выполнить экспериментальную проверку некоторых положений теории двухполюсников. Краткие сведения из теории
Двухполюсником называется электрическая цепь любой сложности, имеющая два зажима (полюса) для присоединения к источнику электрической энергии или к другой электрической цепи. Если сопротивления или проводимости двух двухполюсников, имеющих различные схемы, равны друг другу во всем диапазоне частот от w = 0 до w ® ¥, то двухполюсники называются эквивалентными. Обратными называются два двухполюсника, имеющие различные схемы, если произведение их сопротивлений или проводимостей является постоянной величиной, не зависящей от частоты. Двухполюсники, состоящие только из индуктивностей и емкостей, называются реактивными. Двухполюсники, которые содержат наименьшее количество элементов при заданном числе резонансных частот, называются приведенными. В приведенном двухполюснике уменьшение числа элементов вызывает изменение характера частотной зависимости сопротивления. Сопротивление реактивного двухполюсника с увеличением частоты всегда растет (в алгебраическом смысле), поэтому резонансы напряжения и тока всегда чередуются. При отсутствии потерь сопротивление двухполюсника на частоте резонанса тока становится бесконечно большим и падение напряже- ния достигает максимального значения, а при резонансе напряжения Z(jwp) = 0 и напряжение минимально.
2.1.1. Основные свойства приведенных реактивных двухполюсников
Перечислим эти свойства: 1) число резонансных частот - на единицу меньше числа элементов; 2) если в схеме двухполюсника есть путь постоянному току, то первым будет резонанс токов; 3) если в схеме двухполюсника есть путь току высокой частоты, то последним будет резонанс токов; 4) в схеме приведенного двухполюсника число реактивных элементов разного рода не может отличаться больше чем на единицу; 5) при четном числе элементов последний резонанс имеет тот же характер, что и первый. Из трех реактивных элементов, два из которых имеют сопротивления, противоположные по знаку, можно составить четыре различные схемы реактивных двухполюсников, приведенные в табл. 2.1. Каждый из этих двухполюсников имеет два резонанса: резонанс токов и резонанс напряжений. Для четырехэлементных двухполюсников число резонансов увеличивается до трех: два резонанса напряжений и один резонанс токов или наоборот.
Таблица 2.1
Порядок выполнения работы
2.2.1. Рассчитать и построить частотную зависимость сопротивления одного из трехэлементных (четырехэлементных) двухполюсников (по указанию преподавателя), выбрав самостоятельно по четыре – пять значений частоты в каждом из трех диапазонов для трехэлементного двухполюсника (четырех – для четырехэлементного):
0 £ w < w1; w1 £ w <w2; w2 £ w < ¥. (2.1)
2.2.2. Определить экспериментально (с помощью ПК) резонансные частоты и характер резонансов, сравнить их с рассчитанными.
2.2.3. Измерить методом двух вольтметров входное сопротивление заданного двухполюсника в диапазоне частоты, полученном при выполнении п. 2.2.2. 2.2.4. Обработать результаты измерений и сопоставить их с теоретическими данными, построив экспериментальную и расчетную кривые на одном графике. 2.2.5. На ПК измерить Z(jw) с помощью моста переменного тока. 2.2.6. Ответить на контрольные вопросы. Содержание отчета
1) Схемы двухполюсника и измерений. 2) Основные расчетные формулы. 3) Зависимости (теоретическая и экспериментальная) реактивной составляющей сопротивления двухполюсника от частоты. 4) Ответы на контрольные вопросы. 2.5. Контрольные вопросы
1) Как определить резонансную частоту по известной схеме двухполюсника? 2) Какие двухполюсники называются эквивалентными? 3) Какие двухполюсники называются потенциально эквивалентными? 4) По какому принципу выполняется приведение двухполюсников? 5) Начертите схему двухполюсника по заданной преподавателем характеристике. 6) Начертите характеристику и запишите формулу сопротивления двухполюсника по заданной преподавателем схеме. 7) Какие двухполюсники называются приведенными, обратными, потенциально обратными?
Лабораторная работа 3 ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ПАРАМЕТРОВ ЧЕТЫРЕХПОЛЮСНИКА Ц е л ь р а б о т ы - изучить собственные параметры четырехполюсника (ЧП) и методы их определения, закрепить теоретический материал на практике. Краткие сведения из теории При передаче сигналов всегда приходится иметь дело с очень сложными электрическими системами. На практике в большинстве случаев нет необходимости интересоваться всеми процессами, протекающими внутри сложной системы, передающей сигналы. Достаточно знать те процессы и то электрическое состояние, которые имеют место на ее входе и выходе, что позволяет правильно оценить режимы работы передатчика и приемника. Такая постановка вопроса позволяет достаточно просто выявить общие характеристики, необходимые для оценки передающих свойств большого количества схем, различных по типу и внутренней структуре, облегчая тем самым их сравнение в условиях эксплуатации, поэтому при изучении электрической системы как некоторой среды, в которой распространяется энергия электрических сигналов, ее можно представить себе в виде коробки, имеющей четыре зажима: 1, 1¢, 2, 2¢ (рис. 3.1). Зажимы ЧП, к которым присоединяется источник электрической энергии (генератор), называются входными, а зажимы, к которым присоединяется нагрузка (приемник), - выходными. При изменении направления передачи сигналов роль зажимов соответственно изменяется.
а б
Рис. 3.1. Направления тока и напряжения, принятые при изучении четырехполюсников
Четырехполюсник называется активным, если он содержит внутри себя источники электрической энергии. При этом, если источники являются независимыми, на одной или обеих парах разомкнутых зажимов линейного ЧП обязательно имеется напряжение, т. е. действие источников внутри ЧП взаимно не компенсируется. Четырехполюсники, не содержащие источников энергии, а также линейные ЧП с независимыми взаимно компенсирующимися источниками, называются пассивными. Четырехполюсники называются эквивалентными, если при их взаимной замене в электрической цепи ток и напряжение в остальной части цепи не изменяются. Если перемена местами входных и выходных зажимов не изменяет тока и напряжения в цепи, с которой соединен ЧП, такой ЧП является симметричным. В противном случае ЧП будет несимметричным. Взаимное соотношение между напряжениями и токами на входе (
где А11, А12, А21, А22 – коэффициенты уравнений передачи ЧП, зависящие от его схемы и частоты, но не зависящие от Физический смысл коэффициентов уравнений передачи ЧП наглядно раскрывается при анализе режимов холостого хода и короткого замыкания. Безразмерные коэффициенты А11 и А22 характеризуют соответственно передачу напряжения и тока через ЧП: при холостом ходе –
при коротком замыкании –
Коэффициент А12 представляет собой сопротивление передачи в режиме короткого замыкания, т. е.
а передаточная проводимость при холостом ходе
В пассивном четырехполюснике
в симметричном – А11 = А22. (3.7)
Кроме собственных параметров – коэффициентов (А), (В), (Z), (Y), (H), (G) – четырехполюсник характеризуется характеристическими параметрами:
Характеристическим сопротивлением Zс1 называется входное сопротивление ЧП при прямом направлении передачи, когда к выходным зажимам 2 – 2¢ в качестве нагрузки подключено сопротивление Zс2 (и наоборот). Условие, когда четырехполюсник нагружен на соответствующее характеристическое сопротивление, называется условием согласованной нагрузки. Комплексный параметр gс называется постоянной (мерой) передачи. Его вещественную часть, характеризующую изменение амплитуды мощности, называют собственным затуханием, а мнимую, равную полусумме фазовых сдвигов между напряжениями и токами соответственно на входе и выходе ЧП, – собственной фазовой постоянной. Собственное затухание и фазовый сдвиг (ас и bс) имеют место при передаче сигналов через ЧП в режиме согласованной нагрузки и при расчетах по формуле (3.9) вычисляются в неперах (Нп) и радианах (рад) соответственно.
Основные уравнения передачи энергии в четырехполюснике с учетом соотношений (3.8) и (3.9) можно записать через его характеристические параметры:
Входное сопротивление несимметричного ЧП зависит от его параметров, нагрузки и направления передачи энергии. При прямом направлении
при обратном – где I¢2, U¢2 и Z¢н – ток, напряжение на входе ЧП и сопротивление нагрузки при обратном направлении передачи (см. рис. 3.1, б). На основании соотношений (3.9) – (3.12) в режиме холостого хода имеем:
в режиме короткого замыкания –
а также где х, у – вещественная и мнимая части комплексного числа
Так как
то, если известны входные сопротивления четырехполюсника в режимах холостого хода и короткого замыкания, для расчета характеристических параметров и коэффициентов А11, А12, А21, А22 на основании выражений (3.6), (3.13) – (3.17) можно вывести следующие формулы:
bс = j/2; (3.22)
где
j - угол комплексного числа
При расчете по формулам (3.21), (3.22) затухание получается в децибелах, а фазовый сдвиг – в градусах. Кроме того, следует помнить, что гиперболический тангенс комплексного аргумента является многозначной функцией. Поэтому, к углу, вычисленному по формуле (3.22), следует прибавить K×180°, где К – целое число (0, 1, 2, 3, …). Порядок выполнения работы 3.2.1. Изучить физический смысл параметров ЧП [1, 2]. 3.2.2. Измерить мостом переменного тока, используя ПК и программу «Лабораторные работы по ТЛЭЦ», входное сопротивление ЧП при прямом и обратном направлениях передачи в двух режимах: а) холостой ход, б) короткое замыкание (всего четыре). Внимание. Запрещается выходить из программы без разрешения преподавателя. 3.2.3. Рассчитать собственные параметры ЧП по результатам измерений входного сопротивления при холостом ходе и коротком замыкании, определить вид схемы замещения и параметры элементов. 3.2.4. Собрать схему на лабораторном макете. 3.2.5. Определить коэффициенты основных уравнений передачи и собственное затухание ЧП методом уровней. 3.2.6. Сравнить результаты обоих использованных методов, оценить их достоинства и недостатки. 3.2.7. Ответить на контрольные вопросы. Рис. 3.2. Схема измерения собственного затухания
2) Измерить уровни передачи на входе и выходе ЧП. 3) Рассчитать собственное затухание ЧП по формуле:
где Рвх, Рвых – абсолютные уровни напряжения на входе и выходе ЧП соответственно, дБ. При обратном направлении передачи сопротивления Zс1 и Zс2 меняются местами (или изменяется знак последнего слагаемого). 4) Сравнить данные эксперимента, полученные по формуле (3.28), с результатом расчета ас по формуле (3.21). 3.3.4. Определение коэффициентов основных уравнений передачи методом уровней
1) Собрать на лабораторном макете схему, приведенную на рис. 3.3, а, для чего необходимо дополнить схему измерения собственного затухания (см. рис. 3.2) сопротивлением RШ1. Значение RШ1 принять равным 2 % от меньшего из входных сопротивлений короткого замыкания и холостого хода (
а
б
Рис. 3.3. Схема определения коэффициентов уравнений передачи методом уровней 2) Измерить уровни напряжения на входе и выходе ЧП, а также на RШ1, подключая измерительный прибор с помощью соединительных проводов к соответствующим клеммам макета в режимах холостого хода и короткого замыкания (всего пять отсчетов). Значения токов вычислите по закону Ома, используя падение напряжения на RШ1. 3) Собрать схему, приведенную на рис. 3.3, б, и измерить уровень напряжения на сопротивлении RШ2. 4) Вывести формулы (А)-коэффициентов через уровни. Рассчитать числовые значения этих параметров по измеренным уровням напряжения. 5) Сопоставить полученные результаты с данными расчета в п. 3.3.2. Сделать выводы и записать в отчет.
Содержание отчета 1) Схемы измерений и основные расчетные формулы. 2) Результаты измерений и расчетов. 3) Ответы на контрольные вопросы.
3.5. Контрольные вопросы 1) Каков физический смысл коэффициентов уравнений передачи сигналов? 2) Что такое характеристические параметры, каков их физический смысл? 3) Чем характеристические параметры отличаются от повторных, рабочих? 4) От чего зависит входное сопротивление ЧП? 5) Как записывается условие согласованной нагрузки при прямом и обратном направлениях передачи сигналов через ЧП? 6) Как по результатам измерений определить, является ли ЧП пассивным, симметричным? 7) Как по (А)-матрице различить симметричную и несимметричную схемы ЧП?
Лабораторная работа 4 Краткие сведения из теории Если на выходе ЧП подключена согласованная нагрузка, то условия передачи сигналов определяются его собственными параметрами: характеристическими сопротивлениями, характеристической постоянной передачи (см. лабораторную работу 3). Эти параметры, хотя и полностью характеризуют данный ЧП как некоторую систему для передачи мощности, в общем, не являются достаточно удобными измерителями в эксплуатационных условиях. Это объясняется тем, что условия передачи мощности через ЧП не определяются только собственными его параметрами, но в значительной степени зависят также от тех условий, в которых этот ЧП используется, т. е. от параметров генератора и нагрузки. Эффект передачи сигнала через один и тот же ЧП может существенно изменяться, если изменяются характеристики передатчика и приемника, подключаемых к четырехполюснику. В реальных условиях не удается добиться согласованных включений, так как характеристическое сопротивление ЧП часто имеет сложную частотную зависимость (например, у фильтров, линий связи и др.). В случае несогласованности в точках соединения возникают отражения, влияние которых учитывается введением понятия о рабочем затухании. Например, если сопротивление приемника Zн не равно характеристическому сопротивлению ЧП Zс2, то не вся мощность, подошедшая к приемному концу, поступает в нагрузку. Отраженная от нагрузки мощность возвращается к генератору, частично теряясь в элементах ЧП. Для отраженной волны нагрузкой является сопротивление генератора, подключенного к передающему концу. Если сопротивление генератора не равно характеристическому сопротивлению Zс1, то происходит частичное отражение энергии, причем новая отраженная волна будет распространяться от генератора к приемнику. Многократное отражение энергии при несогласованных нагрузках на обоих концах ЧП приводит к дополнительному рассеиванию энергии, ухудшению качества передачи и появлению амплитудно-частотных и фазочастотных искажений сигнала. Для улучшения условий передачи сигналов (уменьшения искажений и потерь электрической энергии) необходимо обеспечить полную согласованность сопротивления приемника с характеристическим сопротивлением ЧП, т. е. равенство их как по модулю, так и по углу. Рабочее затухание ЧП позволяет оценить тракт передачи в рабочих условиях. Оно включает в себя потери мощности как в самом ЧП, так и по концам его, возникающие вследствие несогласованности сопротивлений приемных и передающих устройств с характеристическими сопротивлениями ЧП. Рабочее затухание представляет собой логарифмическую меру отношения двух мощностей, дБ:
где
а б Рис. 4.1. Схема определения рабочего затухания
Если обозначить (как на рис. 4.1, а) Е – ЭДС генератора, Zг – его внутреннее сопротивление, то
Мощность, поглощаемая приемником Zн, включенном на выходе ЧП (рис. 4.1, б),
Подставляя значения мощностей
или
где Zг – сопротивление генератора, Ом; Zс1, Zс2 – комплексные характеристические сопротивления ЧП, Ом; Zн – сопротивление нагрузки, Ом; ас – собственное затухание ЧП, дБ; jс – характеристическая фазовая постоянная передачи, град;
ао.г – затухание, обусловленное несогласованностью сопротивления генератора с характеристическим сопротивлением ЧП, дБ; ао.н - затухание, обусловленное несогласованностью характеристического сопротивления ЧП с сопротивлением нагрузки, дБ; авз - затухание, обусловленное взаимодействием отраженных волн, дБ. Затухание При
В остальных случаях, когда На основании формулы (4.4) и понятия абсолютного уровня можно получить также выражение, позволяющее определять значение рабочего затухания при экспериментальных исследованиях:
или
где РЕ/2 - абсолютный уровень половины ЭДС генератора; РU – абсолютный уровень напряжения на нагрузке, включенной на выходе четырехполюсника.
Порядок выполнения работы
4.2.1. Изучить рабочие параметры ЧП [1, 2]. 4.2.2. Рассчитать рабочее затухание ЧП, используя характеристические параметры, полученные при выполнении лабораторной работы 3. Сопротивление генератора принять равным 600 Ом, сопротивление нагрузки Zн = КZс, где К - коэффициент. Вариант значений коэффициента К указывается преподавателем: 1) 0,01; 0,21; 0,75; 1; 1,4; 10; 100; 2) 0,015; 0,12; 0,62; 1; 1,5; 30; 150; 3) 0,018; 0,25; 0,51; 1; 2; 50; 120; 4) 0,012; 0,15; 0,68; 1; 1,7; 20; 130. 4.2.3. Измерить рабочее затухание исследуемого ЧП, используя метод уровней. 42.4. Обработать результаты измерений и сопоставить их с теоретическими данными, построив кривые на одном графике (на миллиметровой бумаге). 4.2.5. Ответить на контрольные вопросы.
Рис. 4.2. Схема измерения рабочего затухания
2) Измерить уровень половины ЭДС генератора РЕ/2, для чего необходимо соединить непосредственно генератор и указатель уровня, входное сопротивление которого Zвх у.у, и выполнить условие: Zг = Zвх у.у = 600 Ом (см. рис. 4.1, а). Значение РЕ/2 целесообразно поддерживать постоянным в течение всей работы с помощью регулятора выходного напряжения. При отсутствии индикатора с Zг = Zвх у.у можно измерять уровень полной ЭДС генератора РЕ, подключая к его разомкнутым зажимам высокоомный вход указателя и вводя в формулу (4.7) поправку на 20 lg2 = 6,07 дБ. 3) Измерить уровень напряжения на нагрузке, включенной на выходе четырехполюсника. Значения сопротивления нагрузки задаются с помощью магазина сопротивлений в соответствии с вариантом выполненного теоретического расчета. Измерительный прибор подключают к нагрузке высокоомным входом. 4) Обработать экспериментальные данные по формуле (4.7) и сравнить их с теоретическим расчетом, выполненным по формуле (4.4), оформив результаты в виде табл. 4.1, 4.2 и иллюстраций.
Таблица 4.1
Теоретическая зависимость рабочего затухания и его составляющих от сопротивления нагрузки
Таблица 4.2
Результаты экспериментальных исследований рабочего затухания
Содержание отчета
1) Основные расчетные формулы и схемы. 2) Результаты измерений и расчетов в виде таблиц. 3) Графики теоретической и экспериментальной зависимости рабочего затухания ЧП от сопротивления нагрузки (построить на миллиметровой бумаге). 4) Ответы на контрольные вопросы.
4.5. Контрольные вопросы
1) Как изменится выражение (4.6), если согласовать сопротивление генератора с характеристическим сопротивлением ЧП? 2) В каких пределах изменяются коэффициенты отражения? 3) Как отличается рабочее затухание ЧП от собственного и вносимого? 4) Какие существуют методы уменьшения рабочего затухания? 5) Какие устройства применяются для согласования ЧП с генератором и нагрузкой? 6) В каких случаях рабочее затухание ЧП равно его повторному затуханию?
Библиографический список
1. К а л л е р М. Я. Теория линейных электрических цепей железнодорожной автоматики, телемеханики и связи / М. Я. Каллер, Ю. В. Соболев, А. Г. Богданов. М.: Транспорт, 1987. 399 с. 2. Л о с е в А. К. Теория линейных электрических цепей / А. К. Лосев. М.: Высшая школа, 1987. 512 с. 3. Б е л е ц к и й А. Ф. Основы теории линейных электрических цепей / А. Ф. Белецкий. М.: Радио и связь, 1986. 400 с. 4. Попов В. П. Основы теории цепей / В. П. Попов. М.: Высшая школа, 2000. 496 с.
Учебное издание КАРПОВА Лилия Андреевна, ПОЛУНИН Валерий Тимофеевич
ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ДВУХПОЛЮСНИКОВ И ЧЕТЫРЕХПОЛЮСНИКОВ
Редактор Т. С. Паршикова
***
Лицензия ИД № 01094 от 28.02.2000. Подписано в печать 00.10.2003 Формат 60 ´ 84 1/16. Бумага писчая. Усл. печ. л.. Уч.-изд. л.. Тираж 150 экз. Заказ
**
Редакционно-издательский отдел ОмГУПСа Типография ОмГУПСа
*
Краткие сведения из теории В процессе изучения основных свойств пассивных электрических цепей, широко применяемых в устройствах железнодорожной телемеханики и связи, наиболее часто приходится выполнять измерения уровней электрических величин и комплексных сопротивлений. Понятие уровня вводится для сужения пределов нормируемых величин из-за того, что при передаче электрических сигналов имеют место большое разнообразие и изменение мощности, напряжения и тока. Уровнем какой-либо величины называется ее логарифмическая мера. Если при определении уровня вычисляется десятичный логарифм отношения исследуемых величин, то он выражается в белах, если натуральный – в неперах. Широко используется при измерениях десятая доля бела – децибел. Имеются три разновидности уровней передачи электрических величин: абсолютные, относительные и измерительные. Абсолютным уровнем называется логарифмическая мера отношения исследуемой величины к величине того же рода, условно принятой за единицу. При измерении исследуемых величин наиболее часто используются уровни напряжения, мощности и тока. Если для определения уровней передачи за единицу приняты величины полной мощности S0 = 1 мВ×А, напряжения U0 = 0,775 В и тока I0 = 1,29 мА при сопротивлении R0 = 600 Ом, то полученные при этом уровни будут абсолютными. Относительным уровнем называется логарифмическая мера отношения исследуемой величины к величине того же рода, взятой в произвольной точке цепи. Измерительным называется абсолютный уровень в рассматриваемой точке цепи, когда к началу ее подведено напряжение с уровнем «0 дБ». Значение абсолютного уровня напряжения может быть измерено специальным прибором – указателем уровня, представляющим собой вольтметр, шкала которого проградуирована в логарифмических единицах, или вычислено по формулам:
Зная уровень напряжения, можно рассчитать уровни тока
и мощности
где U, I, S – напряжение, ток и мощность, измеренные на нагрузке с сопротивлением, равным Z. Электрические цепи устройств автоматики, телемеханики и связи в большинстве случаев имеют комплексные сопротивления. Измерение таких сопротивлений целесообразно выполнять с помощью мостов переменного тока. Четыре плеча моста переменного тока образуются четырьмя сопротивлениями, в одну диагональ включается источник (генератор), в другую - индикатор (рис. 1.1, а). При уравновешивании моста
Z1Z3 = Z2Z4. (1.5)
Это уравнение выражает два условия равновесия моста: 1) произведение полных сопротивлений одной пары противолежащих плеч должно быть равно произведению полных сопротивлений другой пары:
½Z1Z3½ = ½Z2Z4½; (1.6)
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 1161; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.200.226 (0.257 с.) |
 ; (1.1)
; (1.1) . (1.2)
. (1.2) или Z2 = R2) и измерения повторяют, записывая соответствующие показания вольтметров Vх2 и V02.
или Z2 = R2) и измерения повторяют, записывая соответствующие показания вольтметров Vх2 и V02. , (1.10)
, (1.10) ; (1.11)
; (1.11) . (1.12)
. (1.12) , а угол j и модуль |Z| вычисляются по формулам:
, а угол j и модуль |Z| вычисляются по формулам: ; (1.13)
; (1.13) . (1.14)
. (1.14)
 ) и выходе (
) и выходе ( ) определяется структурой ЧП. В линейных системах между ними существует линейная зависимость. Если напряжение и ток нагрузки принять известными, то
) определяется структурой ЧП. В линейных системах между ними существует линейная зависимость. Если напряжение и ток нагрузки принять известными, то
 , (3.1)
, (3.1) ; (3.2)
; (3.2) . (3.3)
. (3.3) , (3.4)
, (3.4) . (3.5)
. (3.5) , (3.6)
, (3.6) (3.8)
(3.8) . (3.9)
. (3.9) (3.10)
(3.10) (3.11)
(3.11) (3.12)
(3.12) (3.13)
(3.13) (3.14)
(3.14) (3.15)
(3.15) (3.16)
(3.16) (3.17)
(3.17) ;
; - входные сопротивления ЧП при прямом направлении передачи в режиме к. з. и х. х. соответственно;
- входные сопротивления ЧП при прямом направлении передачи в режиме к. з. и х. х. соответственно; - то же при обратном направлении передачи.
- то же при обратном направлении передачи. , (3.18)
, (3.18) ; (3.19)
; (3.19) ; (3.20)
; (3.20) ; (3.21)
; (3.21) ; (3.23)
; (3.23) ; (3.24)
; (3.24) ; (3.25)
; (3.25) , (3.26)
, (3.26) ; (3.27)
; (3.27) модуль которого
модуль которого 
 - вспомогательная величина.
- вспомогательная величина.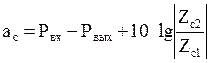 , (3.28)
, (3.28) ): RШ1» 0,02 |Zвх|.
): RШ1» 0,02 |Zвх|.

 , (4.1)
, (4.1) - максимальная активная мощность, которую получает приемник от генератора при непосредственном его подключении к приемнику и при равенстве сопротивлений генератора и приемника;
- максимальная активная мощность, которую получает приемник от генератора при непосредственном его подключении к приемнику и при равенстве сопротивлений генератора и приемника;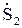 - активная мощность, которую получает от того же генератора приемник с произвольным сопротивлением, включенным на выходе ЧП (рис. 4.1).
- активная мощность, которую получает от того же генератора приемник с произвольным сопротивлением, включенным на выходе ЧП (рис. 4.1).
 . (4.2)
. (4.2) . (4.3)
. (4.3) в формулу (4.1), после некоторых преобразований можно получить выражение для расчета рабочего затухания ЧП через его характеристические параметры и нагрузочные сопротивления, дБ:
в формулу (4.1), после некоторых преобразований можно получить выражение для расчета рабочего затухания ЧП через его характеристические параметры и нагрузочные сопротивления, дБ: (4.4)
(4.4)
 , (4.5)
, (4.5) - коэффициент отражения на передающем конце цепи;
- коэффициент отражения на передающем конце цепи; - коэффициент отражения на приемном конце цепи;
- коэффициент отражения на приемном конце цепи; и зависит от соотношений Zг/Zс1, Zн/Zс2 и собственного затухания ЧП.
и зависит от соотношений Zг/Zс1, Zн/Zс2 и собственного затухания ЧП. и
и  числовое значение
числовое значение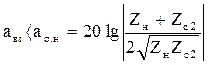 . В этих случаях затухание авз на рабочее затухание ар влияет незначительно и им можно пренебречь, рассчитывая в формуле (4.4) всего три члена.
. В этих случаях затухание авз на рабочее затухание ар влияет незначительно и им можно пренебречь, рассчитывая в формуле (4.4) всего три члена. необходимо учитывать все составляющие рабочего затухания.
необходимо учитывать все составляющие рабочего затухания. (4.6)
(4.6)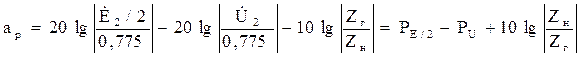 , (4.7)
, (4.7)

 644046, г. Омск, пр. Маркса, 35
644046, г. Омск, пр. Маркса, 35 (1.3)
(1.3) , (1.4)
, (1.4)


