
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм Форда-Фалкерсона. Поток в сети.
Определение 1: Сетью называется связный орграф без петель. Определение 2: Потоком в сети называется некоторая функция, которая ставит в соответствие дуге некоторое число-вес дуги. Для определения потока в сети используют алгоритм Форда-Фалкерсона: а) ищем любую цепь из истока графа в сток; б) каждой дуге приписываем возможный больший поток (наименьшее значение дуги) из истока в сток (записываем его через дробь с весом дуги; при этом поток не может превысить вес дуги, но может быть ему равен); в) если поток становится равен весу дуги, то эта дуга является насыщенной, то есть через нее нельзя пройти при рассмотрении цепей в графе; г) так перебираем все возможные цепи, пока станет невозможно попасть из истока в сток; д) поток в сети будет равен сумме потоков всех дуг, инцидентных стоку графа (следует заметить, что сумма потоков всех дуг, инцидентных стоку графа равна сумме потоков всех дуг, инцидентных истоку графа).
17. Другие задачи которые можно решить с помощью графов (примеры). (!) Поиск A* (произносится «А звезда» или «А стар», от англ. A star) — алгоритм который находит маршрут с наименьшей стоимостью от одной вершины (начальной) к другой (целевой, конечной). Алгоритм Джонсона позволяет найти кратчайшие пути между всеми парами вершин взвешенного ориентированного графа. Алгоритм ближайшего соседа — один из простейших методов решения задачи коммивояжёра. Алгоритм Косарайю (в честь американского учёного индийского происхождения Самбасивы Рао Косарайю (англ.)русск.) — алгоритм поиска компонент сильной связности в орграфе. Алгоритм Мальгранжа — разбиение графов на сильно связные под-графы. Алгоритм Флойда — Уоршелла — динамический алгоритм для нахождения кратчайших расстояний между всеми вершинами взвешенногоориентированного графа.
18. Граф. Основные определения в ТГ (цели, циклы, дуги). Граф — основной объект изучения математической теории графов, совокупность непустого множества вершин и наборов пар вершин (связей между вершинами). Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра[1]. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.
Многие структуры, представляющие практический интерес в математике и информатике, могут быть представлены графами. Например, строение Википедии можно смоделировать при помощи ориентированного графа, в котором вершины — это статьи, а дуги (ориентированные рёбра) — гиперссылки (тематическая карта).
Граф, или неориентированный граф
Ориентированный граф (сокращённо орграф) Дуга — это упорядоченная пара вершин
Прочие связанные определения Маршрутом в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершиной ребром. Цепью называется маршрут без повторяющихся рёбер. Простой цепью называется маршрут без повторяющихся вершин (откуда следует, что в простой цепи нет повторяющихся рёбер). Ориентированным маршрутом (или путём) в орграфе называют конечную последовательность вершин и дуг, в которой каждый элемент инцидентен предыдущему и последующему. Циклом называют цепь, в которой первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер. Заметим, что если вершины Путь (или цикл) называют простым, если ребра в нём не повторяются; элементарным, если он простой и вершины в нём не повторяются.
Логические функции: Основные задачи. Применение. Суть функции. Обозначение. Таблица истинности. Логический смысл.
Логическая функция — это функция логических переменных, которая может принимать только два значения: 0 или 1. В свою очередь, сама логическая переменная (аргумент логической функции) тоже может принимать только два значения: 0 или 1. Основные задачи: - нахождение ИДНФ (Идеальная дизъюнктивная нормальная форма); - ИКНФ (ид Конъюнктивная нормальная форма); - ИАНФ или полином Жегалкина (ид Алгебраическая нормальная форма); - минимизация функции: аналитический метод, метод карт Карно, метод Квайна.. Применение: Логическая функция выполняет логическую операцию или сравнение объектов и выражений, результатом вычисления логической функции будет логическое значение. В многомерных выражениях логические функции крайне важны для определения положения элементов. Они применяются в математической логике и компьютерах и компьютерных науках. Логічних функцій однієї змінної усього чотири. Вони наведені в таблиці 2. Таблиця 2 Логічні функції однієї змінної
Функції j0 і j3 - константи 0 і 1 відповідно; j1 – X; j2 – НЕ X. Логічних функцій двох змінних - 16. Вони наведені в таблиці 3.
Таблиця 3 Логічні функції двох змінних
Функції j0 і j15 константи 0 і 1, тобто функції з двома неістотними змінними. Відзначимо, що ці функції відрізняються від наведених у таблиці 3.2. Там вони унарні, а тут бінарні операції на В. Определим ОСНОВНЫЕ логические функции:
Константы – 1 и 0 соответственно. Инверсия (отрицание) — это логическое не. Говорят, что имея суждение А, можно образовать новое суждение, которое читается как «не А» или «неверно, что А». Для обозначения отрицания суждения употребляется символ или – над переменной. Запись А читается как «не А».
к оньюкция - это логическое умножение. Обозначение: А & В (АВ, А ∧ В). Читается так “ А и В “.
Дизьюкция - это логическое сложение. Обозначение: А ∨ В, (А + В). Читается так: “ А или В ”.
Эквиваленция - это функция тождества. Она обозначается символами =, ~, или <=>. Выбираем обозначение
Импликация - это логическое следование. Импликация двух высказываний А и В соответствует союзу«ЕСЛИ…ТО». Она обозначается символом →. Читается как «из А следует В». Обозначение: A→B. Импликация записывается как посылка Импликация как булева функция ложна лишь тогда, когда посылка истинна, а следствие ложно.
Стре́лка Пи́рса — бинарная логическая операция, булева функция над двумя переменными. Введена в рассмотрение Чарльзом Пирсом (Сharles Peirce) в 1880—1881 г.г. Стрелка Пирса, обычно обозначаемая ↓, эквивалентна операции НЕ-ИЛИ и задаётся следующей таблицей истинности:
Не А, Не B. Пример: здание не высокое, не низкое. Когда оба выражения ложны – функция даст истинный результат. Штрих Ше́ффера — бинарная логическая операция, булева функция над двумя переменными. Введена в рассмотрение Генри Шеффером в 1913 г. Штрих Шеффера, обычно обозначают, как стрелочка вверх и эквивалентен операции НЕ-И. Например, А / В означает: " А и В несовместны" или "Неверно, что А и В". Ещё пример, высказывания "2 х 2 = 4" и "2 х 2 = 5" несовместны. Высказывание со штрихом Шеффера истинно тогда и только тогда, когда либо А ложно, либо В ложно, либо А и В ложны одновременно. Оно ложно и в ом случае, если истинны и А и В одновременно. Действительно, если вместо А подставить высказывание "2 х 2 = 4" и вместо В подставить высказывание "2 х 2 = 4", то А / В дадут ложное высказывание, так как так про идентичные высказывания нельзя сказать, что они несовместны. Таблица истинности со штрихом Шеффера выглядит следующим образом
Сложе́ние по мо́дулю 2 (логи́ческое сложе́ние, исключа́ющее «ИЛИ», строгая дизъюнкция,XOR, поразрядное дополнение, побитовый комплемент, жегалкинское сложение) — булева функция, а также логическая и битовая операция. В случае 2 переменных результат выполнения операции является истинным тогда и только тогда, когда лишь один из аргументов является истинным.
Конъюнкция.
Функція j1 називається кон'юнкцією х1 і х2. Її позначають:
Дизъюнкция.
Функція j7 називається диз'юнкцією х1 і х2. Ії позначають:
Стрелка Пирса.
Стре́лка Пи́рса — бинарная логическая операция, булева функция над двумя переменными. Введена в рассмотрение Чарльзом Пирсом (Сharles Peirce) в 1880—1881 г.г. Стрелка Пирса, обычно обозначаемая ↓, эквивалентна операции НЕ-ИЛИ и задаётся следующей таблицей истинности:
Не А, Не B. Пример: здание не высокое, не низкое. Когда оба выражения ложны – функция даст истинный результат.
23. Штрих Шеффера. (!) Штрих Ше́ффера — бинарная логическая операция, булева функция над двумя переменными. Введена в рассмотрение Генри Шеффером в 1913 г. Штрих Шеффера, обычно обозначают, как стрелочка вверх и эквивалентен операции НЕ-И. Например, А / В означает: " А и В несовместны" или "Неверно, что А и В ". Ещё пример, высказывания "2 х 2 = 4" и "2 х 2 = 5" несовместны. Высказывание со штрихом Шеффера истинно тогда и только тогда, когда либо А ложно, либо В ложно, либо А и В ложны одновременно. Оно ложно и в ом случае, если истинны и А и В одновременно. Действительно, если вместо А подставить высказывание "2 х 2 = 4" и вместо В подставить высказывание "2 х 2 = 4", то А / В дадут ложное высказывание, так как так про идентичные высказывания нельзя сказать, что они несовместны. Таблица истинности со штрихом Шеффера выглядит следующим образом
Константы.
Функції j0 і j15 константи 0 і 1, тобто функції з двома неістотними змінними. (бинарные)
Функції j0 і j3 - константи 0 і 1 відповідно; (унарные) Инверсия. Или отрицание, НЕ
Мнемоническое правило для отрицания звучит так: На выходе будет: «1» тогда и только тогда, когда на входе «0», «0» тогда и только тогда, когда на входе «1» 26. ИКНФ – примеры, назначение. Досконалою кон’юнктивною нормальною формою (ДКНФ) булевої функції називається кон’юнкція тих мінтермів нуля, які перетворюються в нуль на тих самих наборах змінних, що й задана функція. Будуємо з таблиці істинності, відбираючи з неї тільки ті набори, для яких У = 0, та замінюючи в них Хi = 0 змінної Хi, а Хi = 1 - змінної
27. ИДНФ – примеры, назначение. Доскона́лою диз'юнкти́вною норма́льною фо́рмою (ДДНФ) булевої функції називається диз'юнкція тих мінтермів одиниці, які перетворюються в одиницю на тих самих наборах змінних, що й задана функція. Для того, щоб отримати ДДНФ функції, потрібно скласти її таблицю істинності. Фіксуючи увагу тільки на тих наборах, для яких У=1, і замінюючи в них Хi=0 змінної
28. Карта Карно. Применение. (!) У випадку складних функцій від великого числа змінних пошук сусідніх виразів і склеювання їх групи зазначеним вище способом стає скрутним. Метод матриць Карно (діаграм Вейча) полегшує процедуру склеювання завдяки тому, що сусідні члени ДДНФ або ДКНФ, для яких можливо склеювання, розміщаються на площині по сусідству в географічному сенсі. Для функцій n змінних кожна складова канонічної форми може мати n сусідів. Приклади матриць Карно наведені на рис. 2 - 4. X2 X2 X3 0 1 00 01 11 10 X1 X1 0 0 1 0 0 1 3 2
1 2 3 1 4 5 7 6
Рис. 2. Карти Карно для двох і трьох змінних X3 X4 X1 X2 00 01 11 10
00 0 1 3 2
01 4 5 7 6
11 12 13 15 14
10 8 9 11 10 Рис. 3. Карта Карно для чотирьох змінних X3 X4 X5 X1 X2 000 001 011 010 110 111 101 100 (на руку)
00 0 1 3 2 6 7 5 4
01 8 9 11 10 14 15 13 12
11 24 25 27 26 30 31 29 28
10 16 17 19 18 22 23 21 20
Рис. 4 Карта Карно для п'ятьох змінних Кожна клітина матриці відповідає одній комбінації значень вхідних змінних. Код цих комбінацій підібраний так, щоб сусідні клітини відрізнялися значенням тільки однієї змінної, тобто щоб їм відповідали сусідні вирази. Код із такою властивістю називається кодом Грея. У побудовану на основі такого коду таблицю вписуються символи, що відповідають значенням функції на визначених наборах вхідних змінних із таблиці істинності. Якщо в двох сусідніх клітинах заповненої матриці Карно знаходяться однакові символи (0 або 1), то відповідні цим клітинам вирази можна склеювати, що рівнозначно усуненню змінної, яка у рамках групи, що склеюється, змінює значення. Сусідні клітини, що утворюють пари, об'єднуються замкненою лінією для позначення можливості склеювання. Можливі варіанти склеювання для функцій чотирьох змінних наведені на рис. 5.
Рис. 5. Варіанти склеювання для функції чотирьох змінних Розглянемо приклад. Нехай із таблиці істинності отримана ДДНФ, і вона мінімізується аналітичним методом за допомогою склеювання
00 01 11 10 00 1 0 0 1 01 0 0 0 0
11 0 0 0 0 1 0 0 1 Рис. 6. Матриця Карно для приклада
Методика мінімізації логічних функцій за допомогою карт Карно використовується при автоматизованому проектуванні вузлів сучасних ЕОМ і розробці логічних моделей об'єктів і процесів гірничо-металургійного виробництва.
29. Основные законы упрощения логических функций. (!) 1. Закон двойного отрицания (двойное отрицание исключает отрицание): А = 2. Переместительный (коммутативный) закон: o для логического сложения: А Ú B = B Ú A; o для логического умножения: A & B = B & A. Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания. 3. Сочетательный (ассоциативный) закон: o для логического сложения: (А Ú B) Ú C = A Ú (B Ú C); o для логического умножения: (A & B) & C = A & (B & C). При одинаковых знаках скобки можно ставить произвольно или вообще опускать. 4. Распределительный (дистрибутивный) закон: o для логического сложения: (А Ú B) & C = (A & C) Ú (B & C); o для логического умножения: (A & B) Ú C = (A Ú C) & (B Ú C). Закон определяет правило выноса общего высказывания за скобку. 5. Закон общей инверсии (законы де Моргана): o для логического сложения: o для логического умножения: 6. Закон идемпотентности (от латинских слов idem — тот же самый и potens — сильный; дословно — равносильный): o для логического сложения: А Ú A = A; o для логического умножения: A & A = A. Закон означает отсутствие показателей степени. 7. Законы исключения констант: o для логического сложения: А Ú 1 = 1, А Ú 0 = A; o для логического умножения: A & 1 = A, A & 0 = 0. 8. Закон противоречия: o A & Невозможно, чтобы противоречащие высказывания были одновременно истинными. 9. Закон исключения третьего: o A Ú Из двух противоречащих высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано. 10. Закон поглощения: o для логического сложения: А Ú (A & B) = A; o для логического умножения: A & (A Ú B) = A.
30. Комбинационные схемы: назначение. Пример (любой, не более 5-ти элементов). (!) Комбинационные схемы - это схемы, у которых выходные сигналы Y = (у1, у2,..., уm) в любой момент дискретного времени однозначно определяются совокупностью комбинаций входных сигналов Х = (х1, х2,..., хn), поступающих в тот же момент времени t. Поэтому одним из достоинств комбинационных схем является их высокое быстродействие.
Дальше описание по примеру ниже, но с помощью нашего метода реализации!!! Допустим задано булево выражение: Первый этап: выполняется логическое сложение (т.е. логическая операция ИЛИ), считая входными переменными функции
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 296; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.156.250 (0.118 с.) |

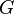 — это упорядоченная пара
— это упорядоченная пара 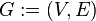 , где
, где 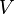 — это непустое множество вершин или узлов, а
— это непустое множество вершин или узлов, а 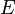 — множество пар (в случае неориентированного графа — неупорядоченных) вершин, называемых рёбрами.
— множество пар (в случае неориентированного графа — неупорядоченных) вершин, называемых рёбрами.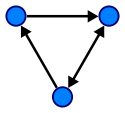
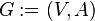 , где
, где  — множество (упорядоченных) пар различных вершин, называемых дугами или ориентированными рёбрами.
— множество (упорядоченных) пар различных вершин, называемых дугами или ориентированными рёбрами. , где вершину
, где вершину  называют началом, а
называют началом, а  — концом дуги. Можно сказать, что дуга
— концом дуги. Можно сказать, что дуга  ведёт от вершины
ведёт от вершины 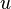 и
и  является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия.
является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия. следствие;
следствие; або
або  &
&  . У всіх випадках знак кон'юнкції аналогічно знаку множення часто опускають і пишуть х1 х2. Вона дорівнює 1, тільки якщо х1 і х2 рівні 1, тому її часто називають функцією І. Ще одна її назва - "логічне множення", оскільки її таблиця дійсно збігається з таблицею звичайного множення для чисел 0 і 1.
. У всіх випадках знак кон'юнкції аналогічно знаку множення часто опускають і пишуть х1 х2. Вона дорівнює 1, тільки якщо х1 і х2 рівні 1, тому її часто називають функцією І. Ще одна її назва - "логічне множення", оскільки її таблиця дійсно збігається з таблицею звичайного множення для чисел 0 і 1. або
або  . Вона дорівнює 1, якщо х1 або х2 дорівнює 1 ("або" тут розуміється в неподільному змісті - хоча б одне з двох). Тому її часто називають функцією АБО.
. Вона дорівнює 1, якщо х1 або х2 дорівнює 1 ("або" тут розуміється в неподільному змісті - хоча б одне з двох). Тому її часто називають функцією АБО.


 . Отримані повні диз'юнкції з'єднуються знаками кон'юнкції. Такий варіант представлення зветься досконалою кон'юнктивною нормальною формою (ДКНФ). Для кожної функції він також єдиний.
. Отримані повні диз'юнкції з'єднуються знаками кон'юнкції. Такий варіант представлення зветься досконалою кон'юнктивною нормальною формою (ДКНФ). Для кожної функції він також єдиний. можна отримати кон’юкції, які потрібно об'єднати знаком Ú. Описаний варіант аналітичного представлення функції має назву досконалої диз'юнктивної нормальної форми (ДДНФ). Зі способу її побудови випливає, що кожна функція може мати лише єдине представлення такого виду.
можна отримати кон’юкції, які потрібно об'єднати знаком Ú. Описаний варіант аналітичного представлення функції має назву досконалої диз'юнктивної нормальної форми (ДДНФ). Зі способу її побудови випливає, що кожна функція може мати лише єдине представлення такого виду.

 .
. =
=  &
&  ;
; =
=  .
. ,
,  ,
,  .
. 

 и
и  на соответствующих входах ставят инверторы:
на соответствующих входах ставят инверторы:



