
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы счисления. Назначение. Принципы построения n-мерной системы счисления.Стр 1 из 7Следующая ⇒
Системы счисления. Назначение. Принципы построения n-мерной системы счисления. Система счисления — символический метод записи чисел, представление чисел с помощью письменных знаков. Система счисления: · даёт представления множества чисел; · даёт каждому числу уникальное представление (или, по крайней мере, стандартное представление); · отражает алгебраическую и арифметическую структуру чисел. Системы счисления подразделяются на позиционные, непозиционные и смешанные (в зависимости от того, зависит ли значение числа от позиций его цифр). Принципы построения q-мерной системы счисления: В q-мерной системе счисления цифры располагаются вправо и влево от точки (запятой), разделяющей целую и дробную части. Каждая цифра имеет вес, определяемый степенью основания системы - q. Значение числа понимается как сумма произведений этих цифр, на их веса (весовые коэффициенты) qi (где i - номера позиций соответствующих цифр относительно запятой).. В общем виде число в произвольной системе счисления запишется в форме: Aq = an-1 · qn-1 +... + a1 · q1 + a0 · q0 + a-1 · q-1 + a-2 · q-2 +... + a-m · q-m или
Где: q – целое положительное основание системы счисления (количество цифр в данной с.сч.); i - номера позиций соответствующих цифр относительно запятой. n; m – порядок числа, слева и справа соответственно. n – от 0 (для целой части), m – от -1 (для дробной части). a – цифра числа в системе счисления с основанием q;
Перевод с 2-ичной системы счисления в 10-ичную и наоборот: Правила. Пример. 2 -> 10
Для перевода из 2 в 10, необходимо пронумеровать цифры числа в начальной системе счисления (начиная с 0 в обратном порядке для целой части и с -1 в прямом порядке для дробной) и выполнить сумму произведений цифр начального числа на основу начальной системы счисления (2) в степени, которая соответствует номеру той цифре начального числа, которая участвует в данном произведении. Пример. 106.52 = 1∙22+0∙21+6∙20+5∙2-1 = 4+0+6+2.5 = 12.510
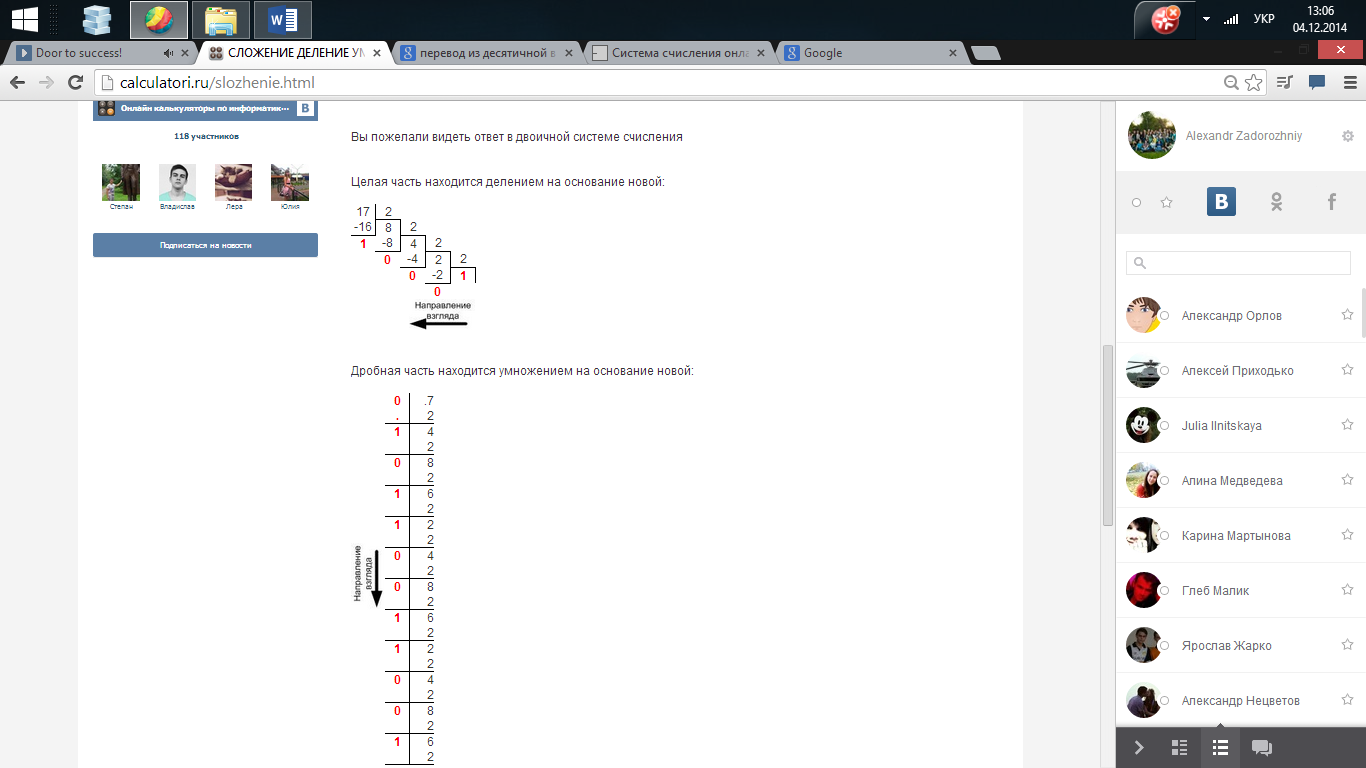
10 -> 2 Для перевода из десятичной СС в двоичную необходимо произвести многократное деление числа на 2 нацело, результатом перевода являются остатки деления, записанные в обратном прядке. Если есть дробная часть, нужно отделить её от целой (0,…) и умножать столбиком на конечную основу систему счисления (2), если результат выше или равен 1-цы, тогда множим основу только на дробную часть результата. Чем больше операций умножения, тем точнее конечный результат дробной части. Дальше в прямом порядке записываем все целые части результатов от умножений и приписываем их к дробной части числа.
Пример. (17.7)d -> (10001.10110011001)b
Перевод с 16-ичной системы счисления в 10-ичную: Правила. Пример. Для перевода из 16 в 10, необходимо пронумеровать цифры числа в начальной системе счисления (начиная с 0 в обратном порядке для целой части и с -1 в прямом порядке для дробной) и выполнить сумму произведений цифр начального числа на основу начальной системы счисления (16) в степени, которая соответствует номеру той цифре начального числа, которая участвует в данном произведении.
Чтобы перевести буквы в числа надо воспользоваться списком: A=10; B=11; C=12; D=13; E=14; F=15
Пример. FF7.A16 = 15∙162+15∙161+7∙160+10∙16-1 = 3840+240+7+0.625 = 4087.62510 Перевод с 16-ичной системы счисления в 2-ичную: Правила. Пример. Разделяем число на отдельные цифры. Каждую цифру по таблице соответствий записываем в двоичной системе, объединяем полученные числа в двоичной системе не меняя порядка записи. Пример. FF7,A = (1111)(1111)(0111), (1010) = 111111110111,101 Множества. Подмножества. Основные понятия. Супермножества. Множества – под множествами понимают объединение элементов в одно общее, это любое собрание определенных и различных между собой элементов, мыслимых как одно целое (рота, группа). Множества могут быть конечными и бесконечными, также множество может не содержать элементов вообще. Во множество может входить один элемент (синглтон). Два множества называются равными, если имеют одни и те же элементы. Каждый элемент входит в множество только один раз. A = {a1, a2, a3, …, an} Подмно́жество в теории множеств — это понятие части множества. Множество
Множество
Универса́льное мно́жество (супермножиство) — в математике множество, содержащее все объекты и все множества. Универсальное множество единственно. Универсальное множество обычно обозначается S, Основные понятия: Мультимножество в математике — обобщение понятия множества, допускающее включение одного и того же элемента по нескольку раз. Число элементов в мультимножестве, с учётом повторяющихся элементов, называется его размером или мощностью. Пустое множество — множество, не содержащее ни одного элемента. Кортеж — упорядоченный набор фиксированной длины. T = {a1, a2, a3, …, an}. Операции над множествами: Основные понятия. Применение. Применение: в информатика, в математики, при работе с базами данных, при анализе данных… Равенство множеств. Множества А и В равны тогда и только тогда, когда каждый элемент множества А является элементом множества В, и наоборот, каждый элемент множества В является элементом множества А, т. е. А Ì В и В Ì А. Объединение множеств. Объединением или суммой двух множеств А и В называется множество, состоящее из всех элементов, каждый из которых принадлежит хотя бы одному из данных множеств. Выполняются законы: S 1)Ассоциативный.
АÈВ=ВÈА; АÈА=А; АÈÆ=А; АÈS=S; АÈВ=А если В Ì А.
Пересечение множеств. Пересечением или произведением двух множеств называется множество, состоящие, из всех тех элементов, которые принадлежат обеим множествам.
S Справедлив коммутативный и ассоциативный закон в частности: А АÇ(ВÈС)=(АÇВ)È(АÇС). В
Два множества А и В являются взаимоисключающими, или несовместимыми, если АÇВ=Æ. Дополнение множеств. Дополнение множества А называется множество, в котором содержатся все элементы пространства S’, кроме принадлежащих множеству А. Оно обозначается через `А. Справедливыми будут следующие выражения = `А А `Æ=S; `S=Æ; (A)=A; AÈ`A=S; AÇ`A=Æ; `AÌ`B при ВÌА; `A=`B если А=В.
Кроме того, справедливы законы де Моргана:
(АÈВ)=`А Ç`В; (АÇВ)=`А È`В.
Разность множеств. Разность А-В множеств А и В есть множество, состоящие из элементов множества А, не принадлежащих множеству В. A - B=A \ B=A Ç`B=A - (AÇB). A S (читаем “A без B”) А-В В
В-А
Из последней диаграммы выведены следующие соотношения: А - Æ = А, А - S = Æ, S - A =`A. Выражения, где присутствует разность, необходимо записывать со скобками. Описанные выше операции со множествами проиллюстрируем примером. Предположим, что элементами пространства S – натуральные числа от 1 до 6. S={1, 2, 3, 4, 5, 6} и определим следующие подмножества: А={2, 4, 6}; B={1, 2, 3, 4}; C={1, 3, 5}. Учитывая приведенные соотношения можно записать: (АÈВ)={1, 2, 3, 4, 6}, (BÈC)={1, 2, 3, 4, 5} (AÈBÈC)={1, 2, 3, 4, 5, 6}=S=AÇC, AÇB={2, 4}, BÇC={1, 3}, AÇC=Æ, AÇBÇC=Æ,`A={1, 3, 5}=C, `B={5, 6}, `C={2, 4, 6}=A, A-B={6}, B-A={1, 3}, A-C={2, 4, 6}=A, C-A={1, 2, 5}=C, B-C={2, 4}, C-B={5}. 7. Законы упрощения операций над множествами. Примеры. (!) Свойства отношений: Симметричность, Транзитивность. Примеры. Матрицы. Симметричность. Отношение ”быть симметричным: если первая точка симметрична второй, то и вторая симметрична первой.
Примеры: Если число a равно числу b, то число b равно числу a. Если высота горы А равна высоте горы В, то и высота горы В равна высоте горы А. Если a+c=b, то и c+b=a.
Транзитивность. Отношение R называется транзитивным, если для любых а, в, с из аRв и вRс следует аRс. Отношения “равенство”, £, “жить в одном городе” транзитивны; отношение “быть сыном” не транзитивно. Примеры: Если число b меньше числа c, а число c меньше числа a, то b меньше a. Если по одной дороге можно дойти от дома до университета, и от университета до магазина, то по той же дороге можно дойти из дома до магазина. Если Аня и Лена одного и того же возраста, а Лена одного возраста с Юлей, то Аня и Юля тоже одногодки.
Отношение называется транзитивным, если
Отношение
Свойства отношений: Еквивалентность. Рефлексивность. Примеры. Матрицы. Рефлексивность. Отношение R называется рефлексивным, если для любого аÎМ имеет место аRа. Главная диагональ его матрицы содержит только единицы. Примеры: Я живу в той же квартире, что и я. В числе 1390 столько же цифр, сколько и в 1390. Масштаб Лондона такой же, как и масштаб Лондона.
Эквивалентность. Отношение называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно. Три равных числа (a=b=c) (Каждое число равно самому себе – рефлексивность; если одно из чисел равно другому, то и другие равные ему числа будут равны этому числу – симметричность; если 1е число равно 2 числу, а 2е число равно 3му, то 1е число тоже равно 3му – транзитивность.) Три горы одной высоты (Каждый гора одной и той же высоты сама с собой – рефлексивность; если 1я гора одной высоты со 2й горой, то остальные горы, которые одной высоты с 1й будут одной высоты и со 2й – симметричность; если 1я гора одной высоты со 2й, а вторая одной и той же высоты с 3й, то 1я тоже одной высоты с 3й – транзитивность.)
Три подруги-одногодки; (аналогично). Анти-свойства и не-свойства. Примеры. Матрицы. Различия. Отношение R называется антирефлексивным, если ни для одного из аÎМ не выполняется аRа. Если условие рефлексивности выполнено не для всех элементов множества Граф. Виды графа. Способы обозначения. Примеры. При изображении графов на рисунках чаще всего используется следующая система обозначений: вершины графа изображаются точками или, при конкретизации смысла вершины, прямоугольниками, овалами и др., где внутри фигуры раскрывается смысл вершины (графы блок-схем алгоритмов). Если между вершинами существует ребро, то соответствующие точки (фигуры) соединяются линией или дугой. В случае ориентированного графа дуги заменяют стрелками, или явно указывают направленность ребра. Иногда рядом с ребром размещают поясняющие надписи, раскрывающие смысл ребра, например, в графах переходов конечных автоматов. ОCНОВНЫЕ виды графов:!!! Граф, или неориентированный граф
Ориентированный граф (сокращённо орграф)
Смешанный граф - связным, если для любых вершин - сильно связным или ориентированно связным, если он ориентированный, и из любой вершины в любую другую имеется ориентированный путь. [Рисунок] - полным, если любые его две (различные, если не допускаются петли) вершины соединены ребром. [Рисунок] - Граф, имеющий конечное множество вершин называют конечным. - Граф, не имеющий ребер, называется пустым. [Рисунок] - взвешенным, если каждому ребру графа поставлено в соответствие некоторое число, называемое весом ребра. [Рисунок] - деревом, если он связный и не содержит нетривиальных циклов. [Рисунок] 13. Матрицы смежности и трансцендентности [скорее инцидентности!?]. Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрица A размера n, в которой значение элемента aij равно наличию ребра из i -й вершины графа в j -ю вершину (1) или его отсутствию (0).
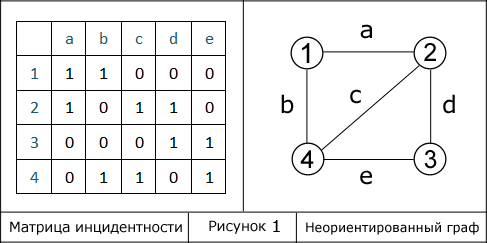
Матрица инцидентности — одна из форм представления графа, в которой указываются связи между инцидентными элементами графа (ребро(дуга) и вершина). 1. Неориентированный граф a. 1 – вершина инцидентна ребру b. 0 – вершина не инцидентна ребру
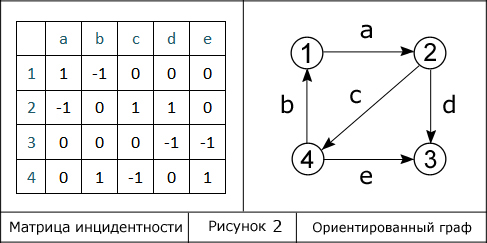
2. Ориентированный граф a. 1 – вершина инцидентна ребру, и является его началом b. 0 – вершина не инцидентна ребру c. -1 – вершина инцидентна ребру, и является его концом Построим матрицу инцидентности сначала для неориентированного графа, а затем для орграфа.
Ребра обозначены буквами от a до e, вершины – цифрами. Все ребра графа не направленны, поэтому матрица инцидентности заполнена положительными значениями.
14. Расчёт сетевого графика. (!) Обозначим: t p - ранний срок наступления события; t n - поздний срок наступления события; t i j - время операций; i - номер предшествующего события; j - номер последующего события; R п - полный резерв времени операции (i, j); R - резерв времени события; t p o - ранний срок окончания операции (i, j); t п о - поздний срок окончания операции (i, j);
Пример. В таблице записаны работы (i, j) и время их выполнения tij;
Начертить сетевой график и найти параметры сетевого графика по событиям и работам.
РЕШЕНИЕ По данным работам i, j строим сетевой график. Событий всего 7, значит рисуем 7 вершин. Надо так расположить вершины, чтобы работы i, j не пересекались.
27 2 4 5 2 2 1 29 10 3 2 12 39 7 0 0 15 39 1 0 5 4 2 5 0 17 8 7 8 8 8 3 0 23 31 8 6 0 t p 31 N R t n
Логические функции: Основные задачи. Применение. Суть функции. Обозначение. Таблица истинности. Логический смысл. Логическая функция — это функция логических переменных, которая может принимать только два значения: 0 или 1. В свою очередь, сама логическая переменная (аргумент логической функции) тоже может принимать только два значения: 0 или 1. Основные задачи: - нахождение ИДНФ (Идеальная дизъюнктивная нормальная форма); - ИКНФ (ид Конъюнктивная нормальная форма); - ИАНФ или полином Жегалкина (ид Алгебраическая нормальная форма); - минимизация функции: аналитический метод, метод карт Карно, метод Квайна.. Применение: Логическая функция выполняет логическую операцию или сравнение объектов и выражений, результатом вычисления логической функции будет логическое значение. В многомерных выражениях логические функции крайне важны для определения положения элементов. Они применяются в математической логике и компьютерах и компьютерных науках. Логічних функцій однієї змінної усього чотири. Вони наведені в таблиці 2. Таблиця 2 Логічні функції однієї змінної
Функції j0 і j3 - константи 0 і 1 відповідно; j1 – X; j2 – НЕ X. Логічних функцій двох змінних - 16. Вони наведені в таблиці 3.
Таблиця 3 Логічні функції двох змінних
Функції j0 і j15 константи 0 і 1, тобто функції з двома неістотними змінними. Відзначимо, що ці функції відрізняються від наведених у таблиці 3.2. Там вони унарні, а тут бінарні операції на В. Определим ОСНОВНЫЕ логические функции:
Константы – 1 и 0 соответственно. Инверсия (отрицание) — это логическое не. Говорят, что имея суждение А, можно образовать новое суждение, которое читается как «не А» или «неверно, что А». Для обозначения отрицания суждения употребляется символ или – над переменной. Запись А читается как «не А».
к оньюкция - это логическое умножение. Обозначение: А & В (АВ, А ∧ В). Читается так “ А и В “.
Дизьюкция - это логическое сложение. Обозначение: А ∨ В, (А + В). Читается так: “ А или В ”.
Эквиваленция - это функция тождества. Она обозначается символами =, ~, или <=>. Выбираем обозначение
Импликация - это логическое следование. Импликация двух высказываний А и В соответствует союзу«ЕСЛИ…ТО». Она обозначается символом →. Читается как «из А следует В». Обозначение: A→B. Импликация записывается как посылка Импликация как булева функция ложна лишь тогда, когда посылка истинна, а следствие ложно.
Стре́лка Пи́рса — бинарная логическая операция, булева функция над двумя переменными. Введена в рассмотрение Чарльзом Пирсом (Сharles Peirce) в 1880—1881 г.г. Стрелка Пирса, обычно обозначаемая ↓, эквивалентна операции НЕ-ИЛИ и задаётся следующей таблицей истинности:
Не А, Не B. Пример: здание не высокое, не низкое. Когда оба выражения ложны – функция даст истинный результат. Штрих Ше́ффера — бинарная логическая операция, булева функция над двумя переменными. Введена в рассмотрение Генри Шеффером в 1913 г. Штрих Шеффера, обычно обозначают, как стрелочка вверх и эквивалентен операции НЕ-И. Например, А / В означает: " А и В несовместны" или "Неверно, что А и В". Ещё пример, высказывания "2 х 2 = 4" и "2 х 2 = 5" несовместны. Высказывание со штрихом Шеффера истинно тогда и только тогда, когда либо А ложно, либо В ложно, либо А и В ложны одновременно. Оно ложно и в ом случае, если истинны и А и В одновременно. Действительно, если вместо А подставить высказывание "2 х 2 = 4" и вместо В подставить высказывание "2 х 2 = 4", то А / В дадут ложное высказывание, так как так про идентичные высказывания нельзя сказать, что они несовместны. Таблица истинности со штрихом Шеффера выглядит следующим образом
Сложе́ние по мо́дулю 2 (логи́ческое сложе́ние, исключа́ющее «ИЛИ», строгая дизъюнкция,XOR, поразрядное дополнение, побитовый комплемент, жегалкинское сложение) — булева функция, а также логическая и битовая операция. В случае 2 переменных результат выполнения операции является истинным тогда и только тогда, когда лишь один из аргументов является истинным.
Конъюнкция.
Функція j1 називається кон'юнкцією х1 і х2. Її позначають:
Дизъюнкция.
Функція j7 називається диз'юнкцією х1 і х2. Ії позначають:
Стрелка Пирса. Стре́лка Пи́рса — бинарная логическая операция, булева функция над двумя переменными. Введена в рассмотрение Чарльзом Пирсом (Сharles Peirce) в 1880—1881 г.г. Стрелка Пирса, обычно обозначаемая ↓, эквивалентна операции НЕ-ИЛИ и задаётся следующей таблицей истинности:
Не А, Не B. Пример: здание не высокое, не низкое. Когда оба выражения ложны – функция даст истинный результат.
23. Штрих Шеффера. (!) Штрих Ше́ффера — бинарная логическая операция, булева функция над двумя переменными. Введена в рассмотрение Генри Шеффером в 1913 г. Штрих Шеффера, обычно обозначают, как стрелочка вверх и эквивалентен операции НЕ-И. Например, А / В означает: " А и В несовместны" или "Неверно, что А и В ". Ещё пример, высказывания "2 х 2 = 4" и "2 х 2 = 5" несовместны. Высказывание со штрихом Шеффера истинно тогда и только тогда, когда либо А ложно, либо В ложно, либо А и В ложны одновременно. Оно ложно и в ом случае, если истинны и А и В одновременно. Действительно, если вместо А подставить высказывание "2 х 2 = 4" и вместо В подставить высказывание "2 х 2 = 4", то А / В дадут ложное высказывание, так как так про идентичные высказывания нельзя сказать, что они несовместны. Таблица истинности со штрихом Шеффера выглядит следующим образом
Константы.
Функції j0 і j15 константи 0 і 1, тобто функції з двома неістотними змінними. (бинарные)
Функції j0 і j3 - константи 0 і 1 відповідно; (унарные) Инверсия. Или отрицание, НЕ
Мнемоническое правило для отрицания звучит так: На выходе будет: «1» тогда и только тогда, когда на входе «0», «0» тогда и только тогда, когда на входе «1» 26. ИКНФ – примеры, назначение. Досконалою кон’юнктивною нормальною формою (ДКНФ) булевої функції називається кон’юнкція тих мінтермів нуля, які перетворюються в нуль на тих самих наборах змінних, що й задана функція. Будуємо з таблиці істинності, відбираючи з неї тільки ті набори, для яких У = 0, та замінюючи в них Хi = 0 змінної Хi, а Хi = 1 - змінної
27. ИДНФ – примеры, назначение. Доскона́лою диз'юнкти́вною норма́льною фо́рмою (ДДНФ) булевої функції називається диз'юнкція тих мінтермів одиниці, які перетворюються в одиницю на тих самих наборах змінних, що й задана функція. Для того, щоб отримати ДДНФ функції, потрібно скласти її таблицю істинності. Фіксуючи увагу тільки на тих наборах, для яких У=1, і замінюючи в них Хi=0 змінної 28. Карта Карно. Применение. (!) У випадку складних функцій від великого числа змінних пошук сусідніх виразів і склеювання їх групи зазначеним вище способом стає скрутним. Метод матриць Карно (діаграм Вейча) полегшує процедуру склеювання завдяки тому, що сусідні члени ДДНФ або ДКНФ, для яких можливо склеювання, розміщаються на площині по сусідству в географічному сенсі. Для функцій n змінних кожна складова канонічної форми може мати n сусідів. Приклади матриць Карно наведені на рис. 2 - 4. X2 X2 X3 0 1 00 01 11 10 X1 X1 0 0 1 0 0 1 3 2
1 2 3 1 4 5 7 6
Рис. 2. Карти Карно для двох і трьох змінних X3 X4 X1 X2 00 01 11 10
00 0 1 3 2
01 4 5 7 6
11 12 13 15 14
10 8 9 11 10 Рис. 3. Карта Карно для чотирьох змінних X3 X4 X5 X1 X2 000 001 011 010 110 111 101 100 (на руку)
00 0 1 3 2 6 7 5 4
01 8 9 11 10 14 15 13 12
11 24 25 27 26 30 31 29 28
10 16 17 19 18 22 23 21 20
Рис. 4 Карта Карно для п'ятьох змінних Кожна клітина матриці відповідає одній комбінації значень вхідних змінних. Код цих комбінацій підібраний так, щоб сусідні клітини відрізнялися значенням тільки однієї змінної, тобто щоб їм відповідали сусідні вирази. Код із такою властивістю називається кодом Грея. У побудовану на основі такого коду таблицю вписуються символи, що відповідають значенням функції на визначених наборах вхідних змінних із таблиці істинності. Якщо в двох сусідніх клітинах заповненої матриці Карно знаходяться однакові символи (0 або 1), то відповідні цим клітинам вирази можна склеювати, що рівнозначно усуненню змінної, яка у рамках групи, що склеюється, змінює значення. Сусідні клітини, що утворюють пари, об'єднуються замкненою лінією для позначення можливості склеювання. Можливі варіанти склеювання для функцій чотирьох змінних наведені на рис. 5.
Рис. 5. Варіанти склеювання для функції чотирьох змінних Розглянемо приклад. Нехай із таблиці істинності отримана ДДНФ, і вона мінімізується аналітичним методом за допомогою склеювання
00 01 11 10 00 1 0 0 1 01 0 0 0 0
11 0 0 0 0 1 0 0 1 Рис. 6. Матриця Карно для приклада
Методика мінімізації логічних функцій за допомогою карт Карно використовується при автоматизованому проектуванні вузлів сучасних ЕОМ і розробці логічних моделей об'єктів і процесів гірничо-металургійного виробництва.
29. Основные законы упрощения логических функций. (!) 1. Закон двойного отрицания (двойное отрицание исключает отрицание): А = 2. Переместительный (коммутативный) закон: o для логического сложения: А Ú B = B Ú A; o для логического умножения: A & B = B & A. Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания. 3. Сочетательный (ассоциативный) закон: o для логического сложения: (А Ú B) Ú C = A Ú (B Ú C); o для логического умножения: (A & B) & C = A & (B & C). При одинаковых знаках скобки можно ставить произвольно или вообще опускать. 4. Распределительный (дистрибутивный) закон: o для логического сложения: (А Ú B) & C = (A & C) Ú (B & C); o для логического умножения: (A & B) Ú C = (A Ú C) & (B Ú C). Закон определяет правило выноса общего высказывания за скобку. 5. Закон общей инверсии (законы де Моргана): o для логического сложения: o для логического умножения: 6. Закон идемпотентности (от латинских слов idem — тот же самый и potens — сильный; дословно — равносильный): o для логического сложения: А Ú A = A; o для логического умножения: A & A = A. Закон означает отсутствие показателей степени.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 468; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.42.94 (0.303 с.) |
 i = -m
i = -m
 является подмножеством множества
является подмножеством множества  , если любой элемент, принадлежащий
, если любой элемент, принадлежащий 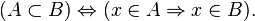
 (от англ. universe, universal set), реже
(от англ. universe, universal set), реже 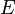 , I.
, I. , т. е.
, т. е.  .
.
 транзитивно.
транзитивно.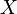 , говорят, что отношение
, говорят, что отношение  нерефлексивно.
нерефлексивно.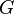 — это упорядоченная пара
— это упорядоченная пара 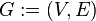 , где
, где 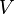 — это не пустое множество вершин или узлов, а
— это не пустое множество вершин или узлов, а 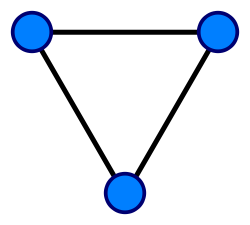
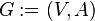 , где
, где 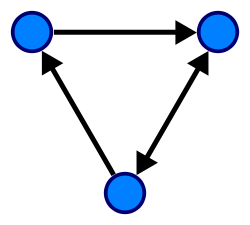
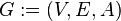 , где
, где 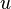 ,
,  есть путь из
есть путь из 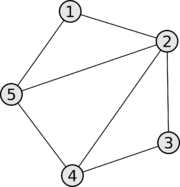
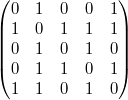
 следствие;
следствие; або
або  &
&  . У всіх випадках знак кон'юнкції аналогічно знаку множення часто опускають і пишуть х1 х2. Вона дорівнює 1, тільки якщо х1 і х2 рівні 1, тому її часто називають функцією І. Ще одна її назва - "логічне множення", оскільки її таблиця дійсно збігається з таблицею звичайного множення для чисел 0 і 1.
. У всіх випадках знак кон'юнкції аналогічно знаку множення часто опускають і пишуть х1 х2. Вона дорівнює 1, тільки якщо х1 і х2 рівні 1, тому її часто називають функцією І. Ще одна її назва - "логічне множення", оскільки її таблиця дійсно збігається з таблицею звичайного множення для чисел 0 і 1. або
або  . Вона дорівнює 1, якщо х1 або х2 дорівнює 1 ("або" тут розуміється в неподільному змісті - хоча б одне з двох). Тому її часто називають функцією АБО.
. Вона дорівнює 1, якщо х1 або х2 дорівнює 1 ("або" тут розуміється в неподільному змісті - хоча б одне з двох). Тому її часто називають функцією АБО.


 . Отримані повні диз'юнкції з'єднуються знаками кон'юнкції. Такий варіант представлення зветься досконалою кон'юнктивною нормальною формою (ДКНФ). Для кожної функції він також єдиний.
. Отримані повні диз'юнкції з'єднуються знаками кон'юнкції. Такий варіант представлення зветься досконалою кон'юнктивною нормальною формою (ДКНФ). Для кожної функції він також єдиний. можна отримати кон’юкції, які потрібно об'єднати знаком Ú. Описаний варіант аналітичного представлення функції має назву досконалої диз'юнктивної нормальної форми (ДДНФ). Зі способу її побудови випливає, що кожна функція може мати лише єдине представлення такого виду.
можна отримати кон’юкції, які потрібно об'єднати знаком Ú. Описаний варіант аналітичного представлення функції має назву досконалої диз'юнктивної нормальної форми (ДДНФ). Зі способу її побудови випливає, що кожна функція може мати лише єдине представлення такого виду.

 .
. =
=  &
&  ;
; =
= 


