
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
С учетом магнитного поля ЗемлиСодержание книги
Поиск на нашем сайте
Распространение волны вдоль магнитного поля Земли Рассмотрим распространение в ионосфере линейно поляризованной ПОВ вдоль направления, совпадающего с направлением вектора магнитного поля Земли Если
- 67 -
где
Из третьего уравнения Максвелла
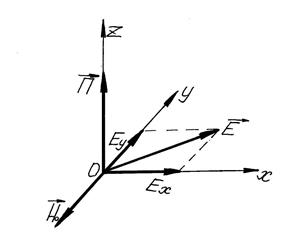
Отсюда следует, что в рассматриваемом случае и Пусть вектор Под действием поля Линейно поляризованную волну можно представить в виде суммы двух волн с противоположными круговыми поляризациями и с амплитудой, равной половине амплитуды линейно поляризованной волны [1]:
Направление вращения вектора - 68 -
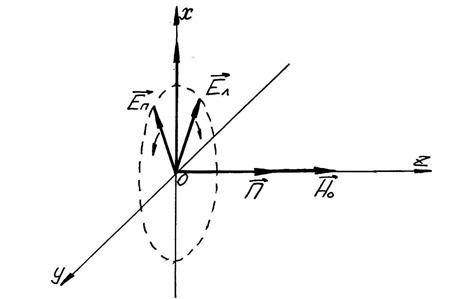
Рис.8.22. Распространение волны вдоль
тора Определим диэлектрические проницаемости ионосферы для этих волн, распространяющихся вдоль магнитного поля Земли. Для волны с правой круговой поляризацией из материального уравнения
Аналогично получаем:
- 69 -
Таким образом, для волны с правой круговой поляризацией диэлектрическая проницаемость ионосферы определяется выражением:
Для волны с левой круговой поляризацией таким же образом получаем:
Эффект Фарадея
Из выражений (8.61), (8.62) очевидно, что и фазовые скорости волн с правой и левой круговыми поляризациями будут различны:
С этим свойством связан эффект Фарадея, смысл которого в том, что при распространении линейно поляризованной волны в ионосфере вдоль магнитного поля Земли происходит поворот плоскости поляризации волны. Запишем мгновенные значения составляющих поля волн с правой (ППВ) и левой (ЛПВ) круговыми поляризациями с начальной нулевой фазой (
ППВ
ЛПВ
- 70 - . Здесь, с учетом (8.63), обозначено:
Используя формулы тригонометрии:
и обозначая:
найдем результирующее поле волны:
Эти две синфазные составляющие в сумме дают поле линейно поляризованной волны, плоскость поляризации которой повернута относительно оси
Рис. 8.23. Поворот плоскости поляризации волны - 71 -
В заключение отметим, что в зависимости от соотношения рону, т.е. угол Распространение волны поперек магнитного поля Земли Рассмотрим ПОВ, распространяющуюся в ионосфере в направлении оси
Рис. 8.24. Распространение волны перпендикулярно Если
где составляющие тензора без учета потерь в ионосфере
- 72 -
Материальное уравнение
а. б. в.
Рассматриваемую волну можно представить в виде суммы двух волн с поперечными составляющими электрического поля Волна, у которой вектор поперечного электрического поля направлен параллельно вектору магнитного поля Земли
т.е. такая же, как для ионосферы без учета Из выражения (8.66 в) следует, что Отсюда вытекает, что волна, вектор поперечного электрического поля которой
- 73 -
Подставляя (8.68) в (8.66 а), получаем связь между перпендикуляр-
ными
Волна, у которой вектор поперечного электрического поля перпендикулярен магнитному полю земли
Различие Аналитические и экспериментальные исследования показали, что при отражении волны в ионосфере распространение можно рассматривать как квазипоперечное [4]. В наиболее интересном случае, когда Если волна падает на ионосферу нормально, то, как было показано в разделе (8.3.3.1.), отражение происходит от слоя, где - 74 -
  
Рис.8.25. Зависимость
Точки отражения необыкновенной волны лежат ниже и выше точки отражения обыкновенной волны, причем луч необыкновенной волны, отражающийся в верхней точке, проходит значительное расстояние в ионосфере. Амплитуда поля этой части необыкновенной волны сильно затухает и на практике может не учитываться. Подобная картина наблюдается и при наклонном падении волны на ионосферу.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 107; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.129.8 (0.01 с.) |

 , без учета потерь (
, без учета потерь ( ).
).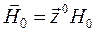 , то тензор диэлектрической проницаемости ионосферы (8.18) принимает вид:
, то тензор диэлектрической проницаемости ионосферы (8.18) принимает вид: ,
, ,
, , (8.59)
, (8.59)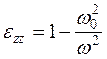 .
. следует, что в ПОВ отсутствует продольная составляющая вектора электрической индукции, и материальное уравнение
следует, что в ПОВ отсутствует продольная составляющая вектора электрической индукции, и материальное уравнение  в координатной форме принимает вид:
в координатной форме принимает вид: ,
, ,
, .
.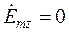 .
. волны лежит в плоскости
волны лежит в плоскости  и направлен вдоль оси
и направлен вдоль оси  (рис. 8.22.).
(рис. 8.22.). .
. (8.60)
(8.60) совпадает с направлением вращения электрона под действием силы Лоренца, а направление вращения век-
совпадает с направлением вращения электрона под действием силы Лоренца, а направление вращения век-
 - противоположно. Отсюда можно сделать вывод, что условия распространения волн с правой и левой круговыми поляризациями различны.
- противоположно. Отсюда можно сделать вывод, что условия распространения волн с правой и левой круговыми поляризациями различны. , имеем:
, имеем:
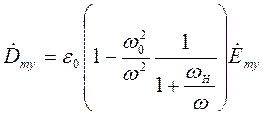 .
. (8.61)
(8.61) . (8.62)
. (8.62) ,
,  (8.63)
(8.63) ), сумма которых дает линейно поляризованную волну (8.60), прошедшую расстояние
), сумма которых дает линейно поляризованную волну (8.60), прошедшую расстояние 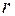 :
: ;
; 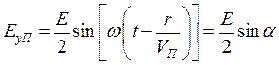 .
.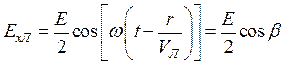 ;
; 
 ,
,  .
.
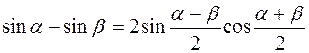
 , (8.64)
, (8.64)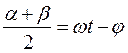 , где
, где  ,
, ,
, .
. на угол
на угол  (рис. 8.23.).
(рис. 8.23.).
 и
и  поворот плоскости поляризации может происходить в ту или другую сто-
поворот плоскости поляризации может происходить в ту или другую сто- перпендикулярно магнитному полю Земли
перпендикулярно магнитному полю Земли  направлен произвольно относительно
направлен произвольно относительно  .
.
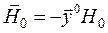 , то тензор диэлектрической проницаемости (8.18) принимает вид:
, то тензор диэлектрической проницаемости (8.18) принимает вид: ,
, представляются формулами:
представляются формулами: ,
, , (8.65)
, (8.65) .
. в координатной форме в этом случае принимает вид, где, как и выше, учтено, что
в координатной форме в этом случае принимает вид, где, как и выше, учтено, что  :
:
 (8.66)
(8.66) .
. 
 и
и  .
. , (8.67)
, (8.67) и
и  .
. :
: . (8.68)
. (8.68) . (8.69)
. (8.69) (8.70)
(8.70) и
и 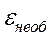 говорит о том, что и условия распространения обыкновенной и необыкновенной волн в ионосфере различны.
говорит о том, что и условия распространения обыкновенной и необыкновенной волн в ионосфере различны. и графики
и графики  и
и 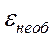 имеют вид, представленный на рис. 8.25., происходит тройное лучепреломление.
имеют вид, представленный на рис. 8.25., происходит тройное лучепреломление. , что соответствует точкам A и C для необыкновенной волны и точке B для обыкновенной волны (рис.8.25.). Обыкновенная волна отражается в том слое ионосферы, где
, что соответствует точкам A и C для необыкновенной волны и точке B для обыкновенной волны (рис.8.25.). Обыкновенная волна отражается в том слое ионосферы, где  (
( ), а необыкновенная волна распадается на два луча с точками отражения в слоях, где
), а необыкновенная волна распадается на два луча с точками отражения в слоях, где 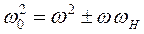 (
( ).
).




