Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распределение энергии в магнитном поле ⇐ ПредыдущаяСтр 2 из 2
Для системы, состоящей из
где
С точки зрения физических представлений о природе электромагнитного поля уместнее говорить о распределении в пространстве энергии магнитного поля с объемной плотностью
В случае изотропной среды (при совпадению по направлению векторов
Полная энергия магнитного поля в объеме
Электромагнитная сила Под электромагнитной силой понимают силу, действующую на проводники с токами, расположенные в магнитном поле. Такие силы называют также электродинамическими. Электродинамическая сила может быть рассчитана при известной зависимости
Как и в случае электрического поля, выбор знака перед производной определяется видом выражения для В качестве иллюстрации рассмотрим уединенный контур с током. Учитывая известные соотношения
получим выражение для силы, стремящейся деформировать контур
или равноценное
При наличии двух контуров с токами их полные потокосцепления
Выражение для энергии магнитного поля двух контуров
с учетом равенства
Тогда сила, стремящаяся изменить взаимное расположение контуров (например, расстояние между ними), определится выражением
В заключение рассмотрим несколько задач, иллюстрирующих изложенный выше теоретический материал.
Задача 1. По сплошному цилиндрическому проводу радиуса
Решение. Линии напряженности магнитного поля, создаваемого током
где
откуда получаем искомую зависимость
Для любой точки вне проводника решение будет отличаться лишь тем, что внутри контура интегрирования протекает весь ток провода
где Так как магнитный поток
Таким образом, внутренняя индуктивность провода
Данное выражение справедливо только при равномерном распределении тока по сечению проводника, то есть при постоянном токе. Отметим также, что внутренняя индуктивность сплошного цилиндрического провода не зависит от его радиуса. Для проводника длиной один метр, изготовленного из материала с магнитной проницаемостью Провод кроме внутренней индуктивности обладает внешней индуктивностью, определяемой магнитным потоком, замыкающимся вне провода. Для расчета величины этого потока необходимо задать геометрические размеры замкнутого контура, по которому протекает ток. В данном случае контур с током замыкается на бесконечности, что соответствует
Задача 2. Кольцевая катушка прямоугольного сечения имеет
Решение. Задачу решаем в предположении, что витки катушки тесно прилегают друг к другу. В этом случае практически все магнитные силовые линии замыкаются внутри обмотки и, имея вид концентрических окружностей, сцепляются со всеми
Магнитный поток сквозь площадку
Используя закон полного тока и выбирая контур интегрирования совпадающим с магнитной силовой линией радиуса r и охватывающей полный ток
Индуктивность катушки равна:
Задачи для практических занятий и самостоятельной подготовки
Ответ: при
Ответ:
4. На рис.2.16 изображены сечения нескольких проводов с токами. Определить величину интеграла
|
||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 278; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.227.76 (0.016 с.) |
 контуров с токами (рис.2.9), энергия
контуров с токами (рис.2.9), энергия 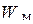 магнитного поля равна
магнитного поля равна
 ,
, 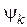 — соответственно ток и потокосцепление
— соответственно ток и потокосцепление  ‑го контура,
‑го контура,  .
.
 ([
([ 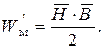
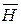 и
и 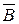 ), имеем соотношения
), имеем соотношения
 определится в виде
определится в виде
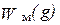 , где
, где  — обобщенная координата (рис.2.9), согласно соотношениям
— обобщенная координата (рис.2.9), согласно соотношениям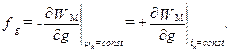
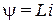 ,
, 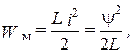
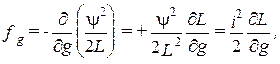
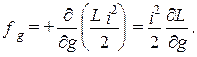
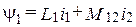 и
и 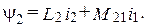

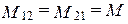 запишется в виде
запишется в виде
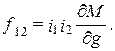
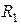 протекает постоянный ток
протекает постоянный ток 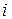 , который распределяется по сечению с постоянной плотностью (рис.2.10). Определить распределение напряженности магнитного поля как функцию расстояния r от оси провода. Рассчитать внутреннюю индуктивность
, который распределяется по сечению с постоянной плотностью (рис.2.10). Определить распределение напряженности магнитного поля как функцию расстояния r от оси провода. Рассчитать внутреннюю индуктивность 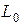 провода.
провода.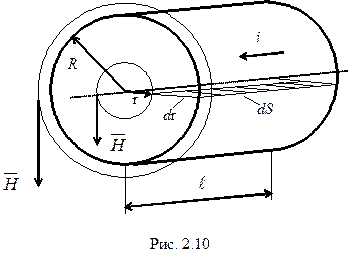
 . Через произвольную точку внутри провода проведем замкнутый контур интегрирования, совпадающий с магнитной силовой линией радиуса r. При таком выборе контура
. Через произвольную точку внутри провода проведем замкнутый контур интегрирования, совпадающий с магнитной силовой линией радиуса r. При таком выборе контура 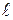 вектора
вектора  совпадают по направлению, и в силу симметрии задачи можем записать
совпадают по направлению, и в силу симметрии задачи можем записать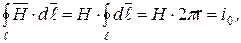
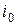 - часть тока провода, протекающего внутри контура
- часть тока провода, протекающего внутри контура  определится как
определится как 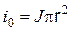 , следовательно
, следовательно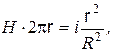
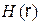 в виде
в виде
 зависимость напряженности магнитного поля от координаты имеет вид
зависимость напряженности магнитного поля от координаты имеет вид
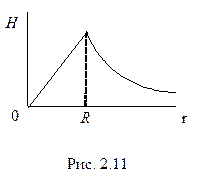 График функции
График функции 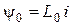 . С целью определения
. С целью определения  рассмотрим элементарный магнитный поток
рассмотрим элементарный магнитный поток  , проходящий через площадку шириной
, проходящий через площадку шириной 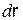 и длиной
и длиной 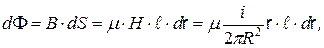
 — магнитная проницаемость материала провода.
— магнитная проницаемость материала провода.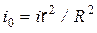 , то полное внутреннее потокосцепление оказывается равным
, то полное внутреннее потокосцепление оказывается равным

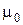 (медь, алюминий), внутренняя индуктивность
(медь, алюминий), внутренняя индуктивность 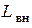 , стремящейся к бесконечности.
, стремящейся к бесконечности. витков (рис.2.12). Определить индуктивность катушки, если ее внутренний и внешний радиусы равны соответственно
витков (рис.2.12). Определить индуктивность катушки, если ее внутренний и внешний радиусы равны соответственно  , а высота
, а высота 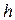 .
.
 где
где  - магнитный поток сквозь поперечное сечение катушки.
- магнитный поток сквозь поперечное сечение катушки.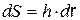 определим как
определим как
 , получаем
, получаем 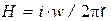 . Выражение для потока
. Выражение для потока  в виде
в виде
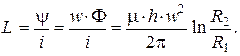
 1. Постоянный ток
1. Постоянный ток 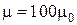 ,
,  = 8
= 8  106 См/м, внешнего (алюминий)
106 См/м, внешнего (алюминий)  ,
,  = 4
= 4 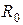 = 5 мм, радиус поверхности раздела сталь-алюминий
= 5 мм, радиус поверхности раздела сталь-алюминий 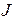 , напряженности магнитного поля
, напряженности магнитного поля 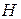 и магнитной индукции
и магнитной индукции  в функции расстояния
в функции расстояния  от оси провода.
от оси провода.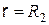
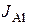 = 2,27
= 2,27  2. Бесконечно длинный провод с током
2. Бесконечно длинный провод с током  и прямоугольная рамка расположены в воздухе в одной плоскости (рис.2.14). Число витков рамки
и прямоугольная рамка расположены в воздухе в одной плоскости (рис.2.14). Число витков рамки 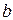 и
и 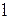 , расстояние от рамки до провода
, расстояние от рамки до провода 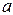 . Определить э.д.с. взаимной индукции в рамке и взаимную индуктивность провода и рамки, если
. Определить э.д.с. взаимной индукции в рамке и взаимную индуктивность провода и рамки, если 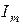 = 5 А,
= 5 А,  = 314 1/с
= 314 1/с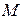 = 3,24
= 3,24  В.
В. 3. Определить взаимную индуктивность рамки с числом витков
3. Определить взаимную индуктивность рамки с числом витков  по замкнутому контуру
по замкнутому контуру