
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача 3. Линейные дифференциальные уравнения первого порядка.Содержание книги
Поиск на нашем сайте
Линейным дифференциальным уравнением первого порядка называется уравнение линейное относительно неизвестной функции и ее производной. Оно имеет вид
где Если
Общее решение неоднородного уравнения можно найти следующими способами: 1) методом вариации произвольной постоянной, который состоит в том, что решение уравнения (1) находится в виде
2) уравнение (1) может быть проинтегрирован с помощью подстановки 3) решение уравнения (1) можно найти еще и по формуле
Замечание. Может оказаться, что дифференциальное уравнение линейно относительно
Пример 4. Решить уравнение Решение. Вид уравнения нормальный
Ответ:
Упражнения. Решить уравнения 1. 2. Приводим к виду 3. 4.
Уравнение линейное относительно функции
ЗАДАНИЯ ПО ВАРИАНТАМ: Решить линейные дифференциальные уравнения первого порядка:
Задача 4. Уравнение Бернулли. Уравнение Бернулли имеет вид
(при Уравнение (1) умножим на
Обозначим Уравнение (2) умножим на
(3) – линейное уравнение относительно переменной Таким образом, уравнение Бернулли можно привести к линейному уравнению. Замечание. Уравнение Бернулли может быть проинтегрировано также методом вариации постоянной, как линейное уравнение и с помощью подстановки Пример 5. Решить уравнение Бернулли Приведем уравнение к виду
Обе части уравнения умножим на
Получили Поэтому Ответ: Упражнения. Решить уравнения
1. 2. 3. Уравнение следует переписать в виде
4. Обе части уравнения следует умножить на ЗАДАНИЯ ПО ВАРИАНТАМ: Решить уравнения Бернулли:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 145; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.79.214 (0.01 с.) |

 (1)
(1) - заданные функции от
- заданные функции от  , непрерывные в той области, в которой требуется проинтегрировать уравнение (1).
, непрерывные в той области, в которой требуется проинтегрировать уравнение (1). , то уравнение (1) называется линейным однородным. Оно является уравнением с разделяющимися переменным и имеет общее решение
, то уравнение (1) называется линейным однородным. Оно является уравнением с разделяющимися переменным и имеет общее решение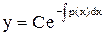 .
.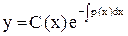 , где
, где  - новая неизвестная функция.
- новая неизвестная функция.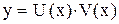 , где
, где  - неизвестные функции от
- неизвестные функции от  .
.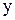 . Нормальный вид (коэффициент при
. Нормальный вид (коэффициент при  равен 1) такого уравнения
равен 1) такого уравнения (
( )
) .
.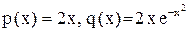 .
.
 .
.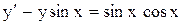 . Ответ:
. Ответ: 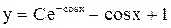 .
.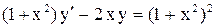 .
.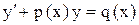 ,
,  и решаем по формуле
и решаем по формуле  . Ответ:
. Ответ: 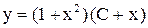 .
.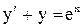 . Ответ:
. Ответ: 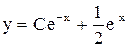 .
. . Ответ:
. Ответ: 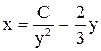 .
.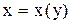 . Приводим его к виду
. Приводим его к виду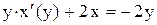 или
или  .
.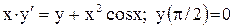 .
.
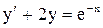 .
.
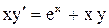 ;
; 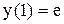 .
.
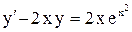 .
.
 .
.
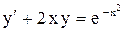 .
.
 .
.
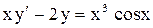 .
.
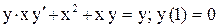 .
.
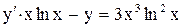 .
.
 .
.
 .
.
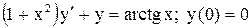 .
.
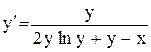 .
.
 .
.
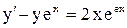 .
.
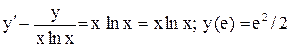 .
.
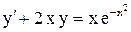 .
.
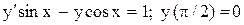 .
.
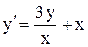 .
.
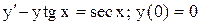 .
.
 .
.
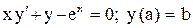 .
.
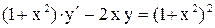 .
.
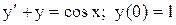 .
.
 .
.
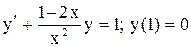 .
.
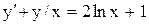 .
.
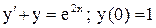 .
.
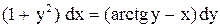 .
.
 (1)
(1) это уравнение является линейным).
это уравнение является линейным).
 (2)
(2) .
.
 или
или (3)
(3) .
. .
.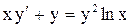 .
.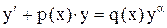
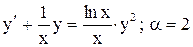 .
.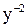 и сделаем замену
и сделаем замену 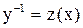 , причем,
, причем, 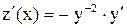 , получим
, получим  - это линейное уравнение относительно
- это линейное уравнение относительно 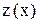 .
.
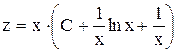 .
. .
.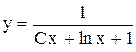 .
. . Ответ:
. Ответ: 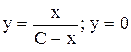 .
.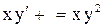 . Ответ:
. Ответ:  .
.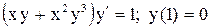 . Ответ:
. Ответ: 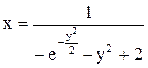 .
.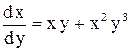 или
или 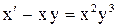 - это уравнение Бернулли относительно функции
- это уравнение Бернулли относительно функции 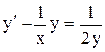 . Ответ:
. Ответ: 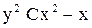 .
. .
. .
.
 .
.
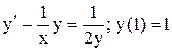 .
.
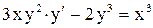 .
.
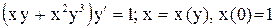 .
.
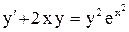 .
.
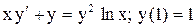 .
.
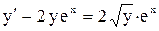 .
.
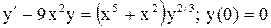 .
.
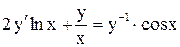 .
.
 .
.
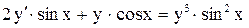 .
.
 .
.
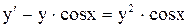 .
.
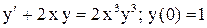 .
.
 .
.
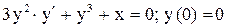 .
.
 .
.
 .
.
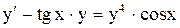 .
.
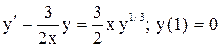 .
.
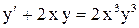 .
.
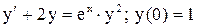 .
.
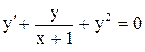 .
.
 .
.
 .
.
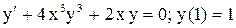 .
.
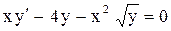 .
.
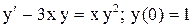 .
.
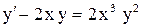 .
.



