
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача 5. Уравнения в полных дифференциалах. ⇐ ПредыдущаяСтр 4 из 4
Дифференциальное уравнение вида
называется уравнением в полных дифференциалах, если его левая часть представляет полный дифференциал некоторой функции
Для того, чтобы уравнение (1) являлось уравнением в полных дифференциалах, необходимо и достаточно, чтобы в некоторой области
В этом случае общий интеграл имеет вид
Пример 6. Решить уравнение Решение. Проверим является ли данное уравнение уравнением в полных дифференциалах
Получили, что Найдем функцию
Из первого уравнения, интегрированием по
где Частная производная
Отсюда
Ответ:
Упражнения. Решить уравнения 1. 2. 3. 4.
ЗАДАНИЯ ПО ВАРИАНТАМ: Проинтегрировать уравнения в полных дифференциалах:
Задача 6. Смешанные задачи на дифференциальные уравнения первого порядка. Смешанные задачи на дифференциальные уравнения первого порядка. Определить тип дифференциального уравнения и указать в общем виде метод его решения: Пример 7. а) б) циалах. в) г) Ответ: Бернулли, Упражнения. Определить тип уравнения и указать в общем виде метод решения: 1.
2. 3. 4. циалах.
ЗАДАНИЯ ПО ВАРИАНТАМ: Определить тип уравнения и указать в общем виде метод решения:
Задача 7. Смешанные задачи на дифференциальные уравнения первого порядка.
Упражнения. Определить тип уравнения и решить его: 1.
2. 3. 4. ЗАДАНИЯ ПО ВАРИАНТАМ: Определить тип уравнения и решить:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 163; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.248.24 (0.019 с.) |
 (1)
(1)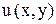 , т.е.
, т.е. .
. изменения переменных
изменения переменных  выполнялось условие
выполнялось условие (2)
(2) или
или .
.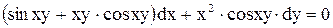 .
.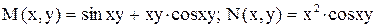 .
.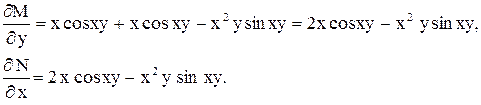
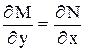 , условие (2) выполнено, значит данное уравнение в полных дифференциалах.
, условие (2) выполнено, значит данное уравнение в полных дифференциалах.
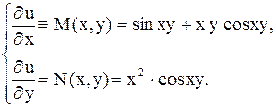
 при постоянном
при постоянном 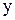 , определяем
, определяем  ,
,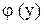 - произвольная функция (вместо постоянной интегрирования С берем функцию
- произвольная функция (вместо постоянной интегрирования С берем функцию  , найденной функции
, найденной функции 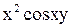 , что дает
, что дает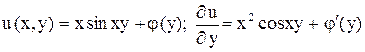 ,
, .
.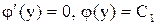 ,
,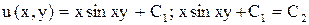 - общий интеграл.
- общий интеграл. , где
, где 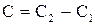 .
.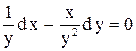 . Ответ:
. Ответ: 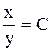 .
. . Ответ:
. Ответ: 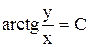 .
.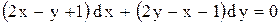 . Ответ:
. Ответ: 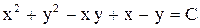 .
. . Ответ:
. Ответ:  .
.
 ,
, уравнение в полных дифференциалах.
уравнение в полных дифференциалах.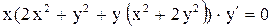 .
.
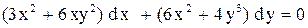 .
.
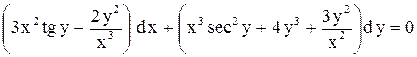 .
.
 .
.
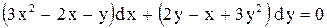 .
.
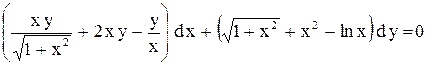 .
.
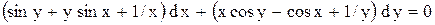 .
.
 .
.
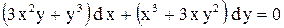 .
.
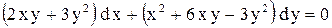 .
.
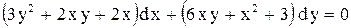 .
.
 .
.
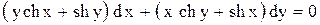 .
.
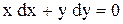 .
.
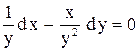 .
.
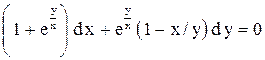 .
.
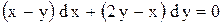 .
.
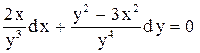 .
.
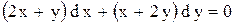 .
.
 .
.
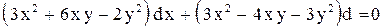 .
.
 .
.
 .
.
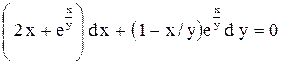 .
.
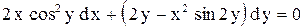 .
.
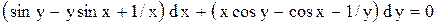 .
.
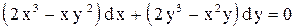 .
.
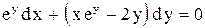 .
.
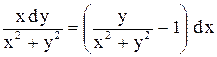 .
.
 .
.
 . Ответ: однородное:
. Ответ: однородное: 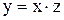 .
. . Ответ: в полных дифферен-
. Ответ: в полных дифферен-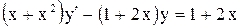 . Ответ: линейное,
. Ответ: линейное,  .
. .
. . Ответ: линейное,
. Ответ: линейное,  .
. . Ответ: Бернулли,
. Ответ: Бернулли,  . Ответ: однородное,
. Ответ: однородное, 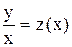 .
. . Ответ: в полных дифферен-
. Ответ: в полных дифферен- .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.

 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
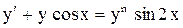 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 . Ответ: с разделяющимися переменными,
. Ответ: с разделяющимися переменными, .
. . Ответ: однородное,
. Ответ: однородное,  .
. . Ответ: линейное,
. Ответ: линейное,  .
. .
. .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
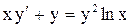 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
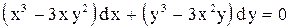 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.



