
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип размерного квантованияСодержание книги Поиск на нашем сайте
Рассмотрим основную идею размерного квантования на примере электронов, находящихся в очень тонкой металлической или полупроводниковой пленке толщиной а. То обстоятельство, что в обычных условиях носители сосредоточены в пленке и не выходят из нее в окружающую среду, означает, что материал пленки (металл или полупроводник) представляет собой потенциальную яму для электронов глубиной, равной работе выхода W, и шириной а. Согласно законам квантовой механики, энергия электронов в такой яме квантуется, то есть может принимать лишь некоторые дискретные значения Еn, где n имеет целочисленные значения 1,2,3,…. Эти дискретные значения называют уровнями размерного квантования. Типичные значения работы выхода в большинстве твердых тел имеют величину W = 4-5 эВ, на несколько порядков превышающую характерную тепловую энергию носителей kТ, равную при комнатной температуре 0.026 эВ. Поэтому потенциальную яму можно считать бесконечно глубокой (рисунок 1 а). Если пленка занимает область 0<z<а, то в этом случае энергетические уровни квантовых состояний выглядят следующим образом:
где m - эффективная масса электрона.
Другим необходимым условием, позволяющим считать яму бесконечно глубокой, является малость значений Еn, по сравнению с ее действительной глубиной W. Это условие, которое для нижних уровней можно записать в виде а>πħ/(2mW)1/2, при m =0.1 m0 соответствует толщинам пленки порядка нескольких межатомных расстояний. Во всех реальных структурах это условие соблюдается. Вывод о квантовании энергии электронного движения относится лишь к движению поперек потенциальной ямы (по оси z). На движение в плоскости ху (параллельно границам пленки) потенциал ямы не влияет. В этой плоскости носители движутся как свободные и характеризуются, как и в массивном образце, непрерывным квадратичным по импульсу энергетическим спектром с эффективной массой m. Полная же энергия носителей в квантово-размерной пленке носит смешанный дискретно-непрерывный спектр, представляя собой сумму дискретных уровней, связанных с движением в направлении квантования, и непрерывной компоненты, описывающей движение в плоскости слоя:
где рx и рy - компоненты импульса в плоскости слоя. Рисунок 1 - Энергетический спектр квантово-размерной пленки
За счет непрерывной компоненты энергетического спектра р2/2m=(px2+py2 )/2m электроны, принадлежащие одному и тому же уровню Еn, могут иметь любую энергию от Еn до бесконечности (рисунок 1 б). Такую совокупность состояний для данного фиксированного n называют подзоной размерного квантования. Пусть все или почти все электроны в системе имеют энергии, меньшие Е2, и потому принадлежат нижней подзоне размерного квантования. Тогда никакой упругий процесс (например, рассеяние на примесях) не может изменить квантовое число n, переведя электрон на вышележащий уровень, так как это потребовало бы дополнительных затрат энергии. Это означает, что электроны при упругом рассеянии могут изменять свой импульс только в плоскости ху, т.е. ведут себя как чисто двумерные частицы. Поэтому квантово-размерные структуры, в которых заполнен лишь один квантовый уровень, часто называют двумерными электронными структурами. Существуют и другие возможные квантовые структуры, где движение носителей ограничено не в одном, а в двух направлениях, как в микроскопической проволоке и нити. В этом случае носители могут свободно двигаться лишь в одном направлении, вдоль нити (например, по оси х). В поперечном сечении (плоскость уz) энергия квантуется и принимает дискретные значения Еmn (как любое двумерное движение, оно описывается двумя квантовыми числами, m и n). Полный спектр при этом тоже является дискретно-непрерывным, но лишь с одной непрерывной степенью свободы:
По аналогии с пленочными структурами, имеющими спектр вида (2), данные системы называются одномерными электронными структурами или квантовыми нитями. Спектр квантовых нитей представляет собой совокупность подзон размерного квантования, но уже не двумерных, а одномерных. Также существуют возможности создать квантовые структуры, напоминающие искусственные атомы, где движение носителей ограничено во всех трех направлениях. Здесь энергетический спектр не содержит непрерывной компоненты, т.е. не состоит из подзон, а является чисто дискретным. Как и в атоме, он описывается тремя дискретными квантовыми числами (не считая спина) и может быть записан в виде Е=Еimn, причем как и в атоме, энергетические уровни могут быть вырождены и зависеть лишь от одного или двух чисел. Подобные системы носят название нуль-мерных электронных структур или квантовых точек. Следовательно, в твердотельных структурах, где хотя бы вдоль одного направления движение носителей ограничено очень малой областью, сравнимой по размерам с дебройлевской длиной волны носителей и характеризуемой обычно десятками нанометров, энергетический спектр носителей заметно меняется и становится частично или полностью дискретным. Подобное изменение спектра за счет размерного квантования приводит к существенному изменению всех электронных свойств системы по сравнению с массивным образцом того же материала.
|
||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 91; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.154.248 (0.007 с.) |

 (1)
(1) (2)
(2)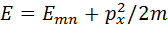 (3)
(3)


