
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика назначения точности возведения строительных конструкций с учетом показателей ответственности зданий.Содержание книги
Поиск на нашем сайте
Как отмечено выше, погрешности при изготовлении деталей, геодезических разбивочных и строительно-монтажных работ, оказывают влияние на точность возведения конструкций зданий. Исследования многих авторов показывают, что распределения погрешностей в размерах и положениях строительных элементов, в основном, соответствуют нормальному закону. Также установлено, что элементарные погрешности в положении строительных элементов и узлов суммируются, а суммарные погрешности регламентируют размеры швов, площадок или уступов между ними, сопрягаемых в единой плоскости. При этом, условия сопряжения строительных элементов обеспечиваются, если положения их не выходят за пределы интервалов соответствующих суммарных допусков. Следовательно, появляется необходимость рассмотрения задачи определения вероятности попадания в заданный интервал нормальной случайной величины [13]:
где s - среднее квадратическое отклонение случайной величины (стандарт); а – математическое ожидание случайной величины; e - основание натуральных логарифмов. Вероятность Р (-¥<х<+¥) =1. Учитывая, что погрешности в положении строительных элементов вызывают изменение несущей способности, прочности и эксплуатационной надежности сборных зданий, возникает необходимость сужения интервалов погрешностей, а это приведет к уменьшению вероятности Р. При уменьшении интервалов от х1 до х2 вероятность появления значений отклонений размеров, лежащих в этих пределах, будет равна:
Введя новую переменную t=(х-а)/s, называемую нормированной, и учитывая, что х=t s+а и dх=s*dt, выражение (2.22) приводится к виду:
где t1=(х1-а)/s; t2=(х2-а)/s. Нормированное распределение позволяет перенести начало координат в центр группирования и к выражению абсцисс в долях s. Пользуясь функцией Лапласа [16]:
получим
Вероятность появления нормируемого значения случайной погрешности в интервале от –t1 до + t2 , с учетом симметричности кривой нормального распределения, будет равна:
Эта вероятность называется доверительной. Следовательно, определение интервалов погрешностей тесно связано с принятием доверительной вероятности. Суммарные погрешности в положении строительных элементов или узлов характеризуются предельными отклонениями d и являются результатом накопления элементарных погрешностей при возведении сборных зданий. Учитывая это, выражение (2.26) можно представить в виде:
Длина доверительного интервала погрешностей при этом будет равна 2 ts. В строительстве при решении практических задач, связанных с нормальным распределением погрешностей, приходится рассматривать попадание в интервал относительно математического ожидания (среднего значения). Тогда выражение (2.27) можно представить так:
Учитывая это, предельные размеры или положения строительного элемента можно выразить:
а тогда допуск размеров или положения будет равен:
Задаваясь различными значения переменной t можно назначить допустимые погрешности с определенной доверительной вероятностью Р. Например, при t= 1; 1,65; 2 и 3 доверительные вероятности принятия интервалов соответственно будут:
Из вышеприведенных выражений видно, что если случайная величина имеет нормальное распределение, то вероятность ее отклонения от своего математического ожидания (среднего значения), не более чем на s составляет 68,27 %, не более, чем на 1,65 s - 90,1 %, не более, чем на 2 s - 95,45 % и не более, чем на 3 s - 99,73 %. Расчетная вероятность Р тесно взаимосвязана с интервалом 2 ts, которая оказывает влияние на размеры площадок опирания, зазоров, т.е. на показатели точности геометрических параметров и на надежность строительных конструкций зданий. Поэтому при установлении границ допускаемых отклонений и допусков геометрических параметров строительных конструкций необходимо учитывать показатели ответственности зданий или надежности конструкций по назначению. Под надежностью строительных конструкций следует понимать способность их выполнять заданные функции в период эксплуатации. Другими словами, надежность можно охарактеризовать как вероятность того, что в заданный период эксплуатации не наступит ни одно из недопустимых предельных состояний для строительных конструкций или их элементов. Способность конструктивных систем выполнять, при заданных условиях возведения и во время эксплуатации, установленные для них функции изучает прикладная теория надежности. Термин «теория надежности» появился в середине 50-ых годов 20-го столетия, хотя расчеты на надежность проводятся уже давно. Расчет конструкций уже по допускаемым напряжениям (классическим методом) представляет собой способ оценки или обеспечения механической надежности. Отечественными учеными были разработаны сначала в 1938 году метод расчета конструкций (бетонных, железобетонных и каменных) по разрушающим нагрузкам, а затем и метод по предельным состояниям. С 1955 года метод расчета по предельным состояниям был введен в действие в СССР в качестве единого метода для расчета строительных конструкций, а с 1962 года - для оснований. При расчетах конструкций по первому предельному состоянию (по несущей способности) в нормах проектирования с 1955 года вместо единого коэффициента запаса были введены три (перегрузок, однородности материалов и условий работы), которые учитывали изменчивость фактических значений нагрузок, прочностных характеристик материалов и условий работы конструкций. Затраты на возведение конструкций в основном зависят от расходов материалов, эксплуатации машин и оборудования, трудозатрат и в меньшей степени от назначения объектов или ответственности зданий. Показатель же надежности существенно зависит от назначения объектов и показателей ответственности зданий. Поэтому в нормах проектирования гидротехнических сооружений в соответствии с главой СНиП II-А.10-71 (Строительные конструкции и основания. Основные положения) с 1971 года вводится 4-й коэффициент ответственности сооружений или надежности по назначению. При проектировании же других конструкций в этот период показатели ответственности сооружений или надежности по назначению не учитывались, т.к. не были установлены. В 1981 году в работе [13] к.т.н. В.А. Отставновым, чл. корр. АН СССР А.Ф. Смирновым, д.т.н. В.Д. Райзером и к.т.н. Ю.В. Суховым рекомендованы показатели ответственности для зданий и сооружений различного назначения. Там же предложено в нормах проектирования строительных конструкций при их расчетах по методу предельных состояний использовать систему частных коэффициентов уже из пяти групп: коэффициенты надежности по нагрузкам, коэффициенты надежности (безопасности) по материалу, коэффициенты условия работы, коэффициенты ответственности зданий и сооружений или надежности их конструкций по назначению и коэффициенты надежности по точности геометрических параметров конструкций. В этом случае главное неравенство при расчете конструкций по первому предельному состоянию – по несущей способности (по прочности или устойчивости), будет иметь вид [13]:
где Nн – усилия от нормативных нагрузок; Ф - функция, соответствующая роду усилия (сжатие, изгиб и т.д.); Si - геометрические характеристики сечения; gfi - коэффициенты надежности по нагрузкам; gmi – коэффициенты надежности по материалу; gdi - коэффициенты условий работ; gni - коэффициенты ответственности зданий и сооружений или надежности конструкций по назначению; gтi - коэффициенты надежности по точности геометрических параметров конструкций. Структура коэффициентов gfi,gmi, gdi достаточно изучена (они применяются с 1955 года). Правила учета степени ответственности зданий и сооружений при проектировании конструкций приведены в [13], а значение коэффициентов надежности по назначению приведены в нормативных документах по расчету строительных конструкций (они применяются с 1981 года). Значения коэффициентов надежности по точности геометрических параметров еще недостаточно изучены. Предлагается допуски на геометрические параметры строительных конструкций при их возведении назначать с учетом показателей ответственности зданий и сооружений. В зависимости от ответственности зданий и сооружений, согласно [13], коэффициенты надежности по назначению gni рекомендовано принимать равными: 1; 0,95 и 0,9. С учетом этих показателей ответственности зданий и сооружений, нормы точности (средние квадратические отклонения) при возведении строительных конструкций предложено назначать [71, 73, 74, 75] при:
При этом размер и положение строительного элемента в процессе изготовления и монтажа может отклоняться от своего проектного или номинального значения (х0) в интервале 2 ts. В этом случае границы этого интервала определяют предельные размеры или положения строительного элемента. В 1988 году введен в действие ГОСТ 27751-88 «Надежность строительных конструкций и оснований. Основные положения по расчету» [13], в которых в 1999 году внесено изменение № 1 по учету ответственности зданий и сооружений. В этом нормативном документе для учета ответственности зданий и сооружений, характеризуемой экономическими, социальными и экологическими последствиями их отказов, установлено три уровня: I - повышенный; II - нормальный; III - пониженный. По ГОСТ 27751-88, повышенный уровень ответственности рекомендовано принимать для зданий и сооружений, отказы которых могут привести к тяжелым экономическим, социальным и экологическим последствиям (резервуары для нефти и нефтепродуктов вместимостью 10000 м3 и более, магистральные трубопроводы, производственные здания с пролетами 100 м и более сооружения связи с высотой 100 м и более, а также уникальные здания и сооружения). Нормальный уровень ответственности рекомендовано принимать для зданий и сооружений массового строительства (жилые, общественные, производственные, сельскохозяйственные здания и сооружения). Пониженный уровень ответственности рекомендовано принимать для сооружений сезонного или вспомогательного назначения (парники, теплицы, летние павильоны, небольшие склады и подобные сооружения). Согласно п.5.2. ГОСТ 27751-88, при расчете несущих конструкций и оснований рекомендовано коэффициент надежности по ответственности gn, принимаемый равный: для I уровня по ответственности – более 0,95,но не более 1,2; для II уровня – 0,95; для III уровня – менее 0,95, но не менее 0,8. В примечании к п.5.2. этого стандарта отмечено, что настоящий пункт не распространяется на здания и сооружения, учет ответственность которых установлен в соответствующих документах. С учетом внесенных изменений в п.5.2. ГОСТ 27751-88, автором предлагается назначать нормы точности (средние квадратические отклонения) при возведении зданий соответственно I, II и III уровней ответственности, определяемых по выражениям (2.36), (2.37) и (2.38).
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 273; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.92.213 (0.007 с.) |

 ,(2.21)
,(2.21) ,(2.22)
,(2.22) , (2.23)
, (2.23)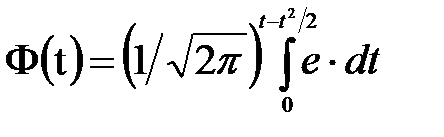 ,(2.24)
,(2.24) . (2.25)
. (2.25) . (2.26)
. (2.26) . (2.27)
. (2.27) . (2.28)
. (2.28) , (2.29)
, (2.29) . (2.30)
. (2.30) ; (2.31)
; (2.31) ; (2.32)
; (2.32) ; (2.33)
; (2.33) . (2.34)
. (2.34) , (2.35)
, (2.35) ; (2.36)
; (2.36)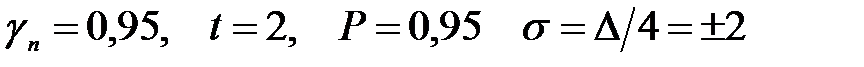 ; (2.37)
; (2.37)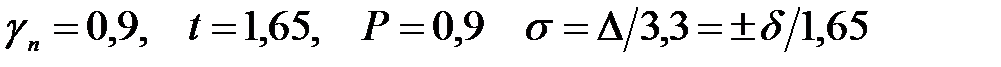 . (2.38)
. (2.38)


