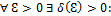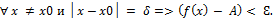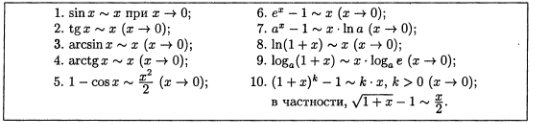Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В первом семестре 2012/2013 учебного годаСодержание книги
Поиск на нашем сайте
ПЕРЕЧЕНЬ ОТВЕТОВ на вопросы по высшей математике, выносимых на экзамен В первом семестре 2012/2013 учебного года 6. Основные понятия векторной алгебры (скалярные и векторные величины, нулевой единичный вектор, орт, коллинеарности, компланарность векторов) Скалярные величины: Величины, которые полностью определяются своим численным значением, называются скалярными. Примерами скалярных величин являются: площадь, длина, объем, температура, работа, масса. Векторные величины: Другие величины, например сила, скорость, ускорение, определяются не только своим числовым значением, но и направлением. Такие величины называют векторными. Векторная величина геометрически изображается с помощью вектора. Вектор — это направленный прямолинейный отрезок, т. е. отрезок, имеющий определенную длину и определенное направление. Нулевым вектором(ō) – называется вектор, у которого начало и конец вектора совпадают, его длина равно нулю. Единичным вектором – называется вектор, длина которого равна единице. Орт: единичный вектор, сонаправленый с вектором ā называется его ортом. Коллинеарность: два ненулевых вектора называются коллинеарными, если они лежат на одной или параллельных прямых. (ā || ƀ) Компланарность: три ненулевых вектора называются компланарными, если они лежат в одной или параллельных плоскостях. Ортогональность: два ненулевых вектора называются ортогональными, если угол между ними равен 90°. (ā ^ ƀ)
Линейные операции над векторами и их свойства. 1) Суммой нескольких векторов a,b,c…d называется вектор i, соединяющий начало первого с концом последнего, если заданные векторы расположены так, что конец предыдущего является началом последующего. 2) Разностью двух векторов ā и ƀ называется третий вектор с который, будучи сложенным с вектором ƀ дает вектор ā. 3) Произведением вектора ā≠0 на скаляр λ≠0 называется вектор, который имеет длину, равную | λ || ā | и сонаправлен с ā, если λ >0, противоположно направлен, если λ <0. Линейные операции обладают такими свойствами: 1) ā+ƀ=ƀ+ā 4) (λ1+λ2) * ā= λ1*ā+ λ2*ā 2) (a+b)+c=a+(b+c) 5) λ*(ā+ƀ)=λ*ā+λ*ƀ 3) λ1*(λ2*ā)= λ1* λ2*ā Скалярное произведение и его совойсва. Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов, на косинус угла между ними: āƀ=|ā||ƀ|cosφ. Свойства: 1) āƀ=ƀā – перестановочное 2) (λā)ƀ=ā(λƀ)=λ(āƀ) – сочетательное 3) a=(b+c)=ab+ac – распределительное 4) ā2=|ā|2 – квадрат вектора равен квадрату его длины 5) ā ^ ƀó āƀ=0 – условие ортогональности векторов 11. *Выражение скалярного произведения через координаты сомножителей.
Приложения скалярного произведения. Приложения:
23.3.) Характеристики: a - большая полуось => 2a – большая ось b - малая полуось => 2b - малая ось с - полуфокусное расстояние. При a > b: Формула связи: b^2 = a^2 – c^2; Фокусы: F1,2 = Эсцентриситет: Ɛ =
Эксцентриситет эллипса – это отношение его полуфокусного расстояния к длине большой оси: Ɛ = Директриса - это прямые, перпендикулярные фокальной оси эллипса и отстоящие от его центра на расстояние x =
Гиперола
Фокусы: F1,2 ( Формула связи: b^2 = c^2 – a^2 Директрисы: x= +- Экс-тет: Асимптоты: y= +- Парабола
26. Различные виды уравнения плоскости (через точку с заданным M0 (x0; y0; z0); 1.) Уравнение прямой проходящей через точку и нормальный вектор: A (x-x0) + B (y-y0) + C (z-z0) = 0; 2.) Общее уравнение прямой на плоскости: Аx + By + Cz + D = 0; (A^2 + B^2 + C^2 3.) В отрезках:
4.) Уравнение прямой проходящей через 3 точки:
Теорема. 1.) Если f(x) – б.б.ф., то 2.) Если 35. * Теорема о связи функции, её предела и б.м.ф. Теорема. Для того чтобы f(x) имела т. x0, предел равный А, необходимо и достаточно, чтобы в окрестности этой точки выполнялось равенство f(x) = A + альфа(x), Альфа(x) – б.м.ф. в т. x0.
(=>) Дано: Доказать: f(x) = A + альфа(x), альфа(x) – б.м.ф. в т. x0.
Если рассмотреть разность f(x) – A как единую функцию, то согласно определению (2) выражение f(x) – A, есть б.м.ф. в т. x0 или f(x) – A = альфа(x) => f(x) = A + альфа(x).
36. *Основные теоремы о пределах (о сумме*,произведении*, частного)
37. *Признак существования предела функции (Теорема о двух милиционерах)
38. *Замечательные пределы
Второй замечательный предел:
39. *Сравнение б.м.ф. Эквивалентные бмф(таблица, теоремы о них)
Таблица эквивалентыности:
ПЕРЕЧЕНЬ ОТВЕТОВ на вопросы по высшей математике, выносимых на экзамен в первом семестре 2012/2013 учебного года 6. Основные понятия векторной алгебры (скалярные и векторные величины, нулевой единичный вектор, орт, коллинеарности, компланарность векторов) Скалярные величины: Величины, которые полностью определяются своим численным значением, называются скалярными. Примерами скалярных величин являются: площадь, длина, объем, температура, работа, масса. Векторные величины: Другие величины, например сила, скорость, ускорение, определяются не только своим числовым значением, но и направлением. Такие величины называют векторными. Векторная величина геометрически изображается с помощью вектора. Вектор — это направленный прямолинейный отрезок, т. е. отрезок, имеющий определенную длину и определенное направление. Нулевым вектором(ō) – называется вектор, у которого начало и конец вектора совпадают, его длина равно нулю. Единичным вектором – называется вектор, длина которого равна единице. Орт: единичный вектор, сонаправленый с вектором ā называется его ортом. Коллинеарность: два ненулевых вектора называются коллинеарными, если они лежат на одной или параллельных прямых. (ā || ƀ) Компланарность: три ненулевых вектора называются компланарными, если они лежат в одной или параллельных плоскостях. Ортогональность: два ненулевых вектора называются ортогональными, если угол между ними равен 90°. (ā ^ ƀ)
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 382; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.208.220 (0.007 с.) |



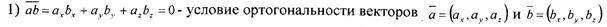


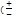 c; 0);
c; 0); < 1;
< 1; :
: - левая.
- левая.
 c;0); F1,2 (0;
c;0); F1,2 (0;  y= +-
y= +- 
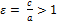
 > 1
> 1

 , общее, в отрезках, через три точки).
, общее, в отрезках, через три точки). (A; B; C).
(A; B; C).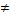 0;
0; ;
;
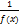 - б.м.ф.
- б.м.ф.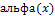 – б.м.ф., непринимающая нулевых значений, то
– б.м.ф., непринимающая нулевых значений, то 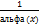 - б.м.ф.
- б.м.ф.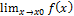 = A ó f(x) = A +альфа(x), альфа(x) – б.м.ф. в т. x0.
= A ó f(x) = A +альфа(x), альфа(x) – б.м.ф. в т. x0.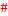 . Т.к.
. Т.к.