
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение простых импликантСодержание книги
Поиск на нашем сайте
Каждый отдельный контур объединения соответствует минтерму, который иначе называют простой импликантой. Для определения и записи простой импликанты, прямо по карте Карно, проводится анализ переменных по тем строчкам и столбцам карты, которые пересекают контур объединенных 1 (вершин куба). Начинают анализ с первой переменной Х1. Если переменная Х1 в любой строчке(столбце), проходящей через контур, не изменяет значения своей координаты (т.е. во всех строчках контура ее значение либо 0, либо 1), то в минтерм объединения записывается ее значение (либо 0, либо1). Если переменная Х1 в строчках (столбцах), проходящих через контур, изменяет значение своей координаты (т.е. в одной строчке контура ее значение 0, а в другой 1, либо наоборот), то в минтерм объединения записывается, так называемая, неопределенная переменная Х на том месте, где должно записываться значение переменной Х1 (рисунок 9.1д,е,ж). Аналогичный анализ проводится последовательно для всех переменных, в результате чего получаем минтерм объединения. На рисунке 9.1д,е,ж они расположены на выносках. Это первый этап записи минимальной логической функции прямо с карты Карно. На втором этапе меняем значения переменных на соответствующие им переменные по правилу: если значение переменной 0 – то пишем При построении минимальной формы для конъюнкции, карты Карно заполняются 0, т.е. минтермами тех наборов, на которых функция равна нулю. Объединение нулей и запись МДНФ для не функции, т.е. Покрытие с минимальной ценой формируется, если каждая существенная вершина будет покрыта кубом с наибольшим числом независимых переменных, а для покрытия всех существенных вершин будет использовано наименьшее число кубов. Наилучшим считается такое покрытие, где минимум контуров объединения. Если вариантов много, то выбирается тот, который дает максимальную суммарную площадь контуров (прямоугольников). Качество минимизации оценивается по коэффициенту покрытия k = m / s, где m - количество прямоугольников, s - их площадь. Покрытие лучше, чем меньше k. В качестве примера использования карт Карно для определения минимальных ДНФ и КНФ рассмотрим функцию, представленную на рисунке 6.5.
Данной ДНФ (рисунок 6.5 а) соответствует минимальная форма вида: f= Нулевые значения этой функции представлены на рисунке 6.5б. Отмеченные на карте клетки определяют функцию При минимизации функции
Используя правило де Моргана, преобразуем в КНФ: f=
|
|||||||
|
Последнее изменение этой страницы: 2016-12-26; просмотров: 717; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.214.1 (0.005 с.) |

 , если 1 – то пишем Хі. На месте неопределенной переменной Х не пишем ничего, т. е. это место опускаем. Тепер соединив все минтермы знаком дизъюнкции, получим минимальную дизъюнктивную нормальную форму логической функции (МДНФ).
, если 1 – то пишем Хі. На месте неопределенной переменной Х не пишем ничего, т. е. это место опускаем. Тепер соединив все минтермы знаком дизъюнкции, получим минимальную дизъюнктивную нормальную форму логической функции (МДНФ). выполняют по тем же правилам. Затем, применив к левой и правой части равенства правило де-Моргана и преобразовав дизъюнкцию правой части в конъюнкцию, получим минимальную конъюнктивную нормальную форму (МКНФ) логической функции. Таким образом,минимальное покрытие выбирается интуитивным путем на основе анализа различных вариантов покрытий (контуров объединений) минимизируемой функции.
выполняют по тем же правилам. Затем, применив к левой и правой части равенства правило де-Моргана и преобразовав дизъюнкцию правой части в конъюнкцию, получим минимальную конъюнктивную нормальную форму (МКНФ) логической функции. Таким образом,минимальное покрытие выбирается интуитивным путем на основе анализа различных вариантов покрытий (контуров объединений) минимизируемой функции.


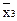 +x1
+x1 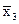 x4+x2x3.
x4+x2x3.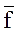 , обратную f.
, обратную f. =
= 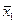 x2
x2  +
+ 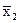 x3.
x3.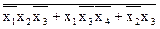 =(x1+
=(x1+ 


