Конъюнкция (логическое умножение)

Если два высказывания соединены союзом "И", то полученное сложное высказывание обычно считается истинным тогда и только тогда, когда истинны оба составляющие его высказывания. Если хотя бы одно из составляющих высказываний ложно, то и полученное из них с помощью союза "И" сложное высказывание также считается ложным.

 

Например, возьмем два высказывания: "У кота есть хвост" (высказывание А), " У зайца есть хвост" (высказывание В).

Сложное высказывание "У кота есть хвост И у зайца есть хвост" истинно, т.к. истинны оба высказывания А и В.

 

Но если взять другие высказывания:

"У кота длинный хвост" (С),

"У зайца длинный хвост" (D),

то сложное высказывание "У кота длинный хвост и у зайца длинный хвост" будет ложным, т.к. ложно высказывание D.

 

Таким образом, исходя из обычного смысла союза "И", приходим к определению соответствующей логической операции - конъюнкции.

 

Конъюнкция – это составное высказывание, образованное логическим умножением. Обозначения конъюнкции: A&B, A∙B, A^B, A and B, A и B.

 

Иными словами, взято два множества: А и В. Умножив А на В, мы получим 0 (ложь), если хотя бы одно из множеств равно нулю.

Значит, высказывание истинно тогда и только тогда, когда истинны (не равны 0) все высказывания, входящие в него. Это видно из таблицы:

В математике: если каждое выражение системы взять за отдельное высказывание то составное высказывание, образованное логическим умножением, будет являться решением этой системы.

Пример: пусть высказывание А – х>5, а высказывание В – х>7 тогда это составное высказывание т.е. х>7.

 

Итак, высказывание A^B можно представить в виде пересечения множеств А и В:

ДИЗЪЮНКЦИЯ (ЛОГИЧЕСКОЕ СЛОЖЕНИЕ)

Если два высказывания соединены союзом " ИЛИ", то полученное сложное высказывание обычно считается истинным, когда истинно, хотя бы, одно из составляющих высказываний.

 

Например, возьмем два высказывания:

«Мел черный» (А), «Доска черная» (В).

Высказывание «Мел черный ИЛИ доска черная» будет истинным, т.к. одно из исходных высказываний (В) истинно.

 

И, напротив, для

«Небо зеленое» (С), «Трава красная» (D)

Высказывание «Небо зеленое ИЛИ трава красная» будет ложным, в силу того, что ложны оба высказывания.

 

Отсюда определение:

Дизъюнкция (логическое сложение) - составное высказывание, образованное логическим сложением,

Обозначения:

A+B, AˇB, А U B

A or B, A или B

 

Дизъюнкция – выражение, истинное тогда и только тогда, когда есть хотя бы одно истинное высказывание, входящее в него:

 

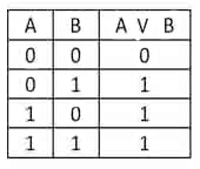В математике: если каждое выражение совокупности взять за отдельное высказывание то составное высказывание, образованное логическим сложением, будет являться решением этой совокупности.

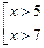Пример: пусть высказывание А – х>5, а высказывание В – х>7 тогда это составное высказывание т.е. х>5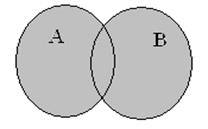

 

Итак, высказывание AˇB можно представить в виде объединения множеств А и В: