
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Инверсия (логическое отрицание)Содержание книги Поиск на нашем сайте
ОГЛАВЛЕНИЕ ГЛАВА 3. ЛОГИКА § 1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ ЛОГИКИ. БУЛЕВА АЛГЕБРА ИНВЕРСИЯ (ЛОГИЧЕСКОЕ ОТРИЦАНИЕ) КОНЪЮНКЦИЯ (ЛОГИЧЕСКОЕ УМНОЖЕНИЕ) ДИЗЪЮНКЦИЯ (ЛОГИЧЕСКОЕ СЛОЖЕНИЕ) ИМПЛИКАЦИЯ (ЛОГИЧЕСКОЕ СЛЕДОВАНИЕ) ЭКВИВАЛЕНЦИЯ (ЛОГИЧЕСКОЕ ТОЖДЕСТВО) § 7. ТАБЛИЦЫ ИСТИННОСТИ § 8. ЛОГИЧЕСКИЕ ФОМУЛЫ. ЗАКОНЫ ЛОГИКИ ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ Упрощение и преобразование формул. Задачник РЕШЕНИЕ ЛОГИЧЕСКИХ ЗАДАЧ I. Решение логических задач средствами алгебры логики. II. Решение логических задач табличным способом. III. Решение логических задач с помощью рассуждений. IV. Задачник ЛОГИКА § 1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ ЛОГИКИ. БУЛЕВА АЛГЕБРА Логика – это наука о формах и способах мышления. Мышление всегда осуществляется в каких-то формах – понятиях, высказываниях, умозаключениях, логических выражениях и т.д. Понятие – форма мышления, фиксирующая основные признаки предмета. Высказывание (суждение) – это предложение, в котором что-то отрицается или утверждается о предмете, его свойствах или отношениях между предметами. Логическое выражение – это либо высказывание, либо несколько высказываний, соединенных логическими операциями. Умозаключение – форма мышления, с помощью которой из одного или нескольких суждений (посылок), можно получить новое суждение (заключение).
Алгебра высказываний (Булева алгебра) была разработана для того, чтобы можно было определять ложность/истинность высказываний, не вникая в их содержание. В соответствие суждению (простому высказыванию) ставятся логические переменные (прописные буквы латинского алфавита). Рассмотрим простое высказывание: A = «Дважды два равно четырем» B = «Дважды два равно пяти»
Иными словами, «А =1, В = 0».
В булевой алгебре мы можем также проводить над высказываниями определенные логические операции, в результате которых, получаются новые, составные высказывания. Наиболее часто используются логические с вязки «и, или, не». Они з аменяются логическими операциями «инверсия, конъюнкция, дизъюнкция», соответственно. Это основные логические операции, при помощи которых можно записать любое логическое выражение. ДИЗЪЮНКЦИЯ (ЛОГИЧЕСКОЕ СЛОЖЕНИЕ) Если два высказывания соединены союзом " ИЛИ", то полученное сложное высказывание обычно считается истинным, когда истинно, хотя бы, одно из составляющих высказываний.
Например, возьмем два высказывания: «Мел черный» (А), «Доска черная» (В). Высказывание «Мел черный ИЛИ доска черная» будет истинным, т.к. одно из исходных высказываний (В) истинно.
И, напротив, для «Небо зеленое» (С), «Трава красная» (D) Высказывание «Небо зеленое ИЛИ трава красная» будет ложным, в силу того, что ложны оба высказывания.
Отсюда определение: Дизъюнкция (логическое сложение) - составное высказывание, образованное логическим сложением, Обозначения: A+B, AˇB, А U B A or B, A или B
Дизъюнкция – выражение, истинное тогда и только тогда, когда есть хотя бы одно истинное высказывание, входящее в него:
Пример:
ТАБЛИЦЫ ИСТИННОСТИ Для каждого составного высказывания (логического выражения) можно построить таблицу истинности, которая определяет его истинность или ложность, при всех возможных комбинациях исходных значений простых высказываний(логических переменных).
При построении таких таблиц целесообразно пользоваться определенной последовательностью действий: 1. Определить количество строк таблицы по формуле: Количество строк = 2n, где n – число логических переменных. 2. Количество столбцов = n + число логических операций. 3. Первые n столбцов нумеруем, начиная с нуля. 4. Заполняем столбец №0 нулями и единицами, чередуя их через 1 знак (номер столбца = 0, 20 = 1); Столбец №1, 21 = 2, чередуем через два знака; Столбец №2, 22 = 4, чередуем через четыре знака и т.д. 5. Заполняем остальные столбцы таблицы истинности, в соответствии с определенным порядком очереди выполнения логических операций: 1. Инверсия
Теперь мы можем определить значение логической функции для любого набора значений логических переменных. § 8. ЛОГИЧЕСКИЕ ФОМУЛЫ. ЗАКОНЫ ЛОГИКИ С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой. В качестве примера рассмотрим высказывание "Если я куплю яблоки или абрикосы, то приготовлю фруктовый пирог" "Если Игорь знает английский или японский язык, то он получит место переводчика". Оба эти высказывания формализуются в виде (A v B) Как показывает анализ формулы (A v B) Некоторые формулы принимают значение "истина" при любых значениях истинности входящих в них переменных. Таковой будет, например, формула А v A, соответствующая высказыванию "Этот треугольник прямоугольный или косоугольный". Эта формула истинна и тогда, когда треугольник прямоугольный, и тогда, когда треугольник не прямоугольный. Такие формулы называются тождественно истинными формулами или тавтологиями. Высказывания, которые формализуются тавтологиями, называются логически истинными высказываниями. В качестве другого примера рассмотрим формулу А &A, которой соответствует, например, высказывание "Катя самая высокая девочка в классе, и в классе есть девочки выше Кати". Очевидно, что эта формула ложна, так как либо А, либо A, обязательно ложно. Такие формулы называются тождественно ложными формулами или противоречиями. Высказывания, которые формализуются противоречиями, называются логически ложными высказываниями. Если две формулы А и В одновременно, то есть при одинаковых наборах значений входящих в них переменных, принимают одинаковые значения, то они называются равносильными. Равносильность двух формул алгебры логики обозначается символом "=" или «º». Замена формулы другой, ей равносильной, называется равносильным преобразованием данной формулы. Равносильности формул логики высказываний часто называют законами логики. Знание законов логики позволяет проверять правильность рассуждений и доказательств. Нарушения этих законов приводят к логическим ошибкам и вытекающим из них противоречиям. Перечислим наиболее важные из них:
Поясним некоторые из них: 1-й закон сформулирован древнегреческим философом Аристотелем. Закон тождества утверждает, что мысль, заключенная в некотором высказывании, остается неизменной на протяжении всего рассуждения, в котором это высказывание фигурирует. Закон противоречия (непротиворечия) говорит о том, что никакое предложение не может быть истинно одновременно со своим отрицанием. Закон исключенного третьего говорит о том, что для каждого высказывания имеются лишь две возможности: это высказывание либо истинно либо ложно. Третьего не дано. “Сегодня я получу 5 либо не получу”. Истинно либо суждение, либо его отрицание. Закон двойного отрицания. Отрицать отрицание какого-нибудь высказывания - то же, что утверждать это высказывание. Законы идемпотентности. В алгебре логики нет показателей степеней и коэффициентов. Конъюнкция одинаковых “сомножителей” равносильна одному из них. XÙ Xº X, XÚ Xº C Законы коммутативности и ассоциативности. Конъюнкция и дизъюнкция аналогичны одноименным знакам умножения и сложения чисел. Смысл законов де Моргана (Август де Морган (1806-1871) - шотландский математик и логик) выразил эти законы в кратких словесных формулировках:
Доказать законы логики можно: 1) с помощью таблиц истинности; Докажем законы склеивания и поглощения с помощью равносильностей: Закон склеивания: (C Ú U) Ù ( º (C + U) × ( º U × º U ( Закон поглощения: C Ù (C Ú U) º C × C +C × U º C +C × U º C (1 + U) º C
Законы логики отражают в сознании человека свойства, связи и отношения окружающих объектов.
ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ Упрощение формул. Пример 1. Упростить формулу (А+В)· (А+С) 2. Преобразования “поглощение” и “склеивание” Пример 2. А) Упростить выражение А+ A · B В) Упростить выражение A · B + A · РЕШЕНИЕ ЛОГИЧЕСКИХ ЗАДАЧ Разнообразие логических задач очень велико. Способов их решения тоже немало. Но наибольшее распространение получили следующие три способа решения логических задач: · средствами алгебры логики; · табличный; · с помощью рассуждений. Пример 1. Трое друзей, болельщиков автогонок "Формула-1", спорили о результатах предстоящего этапа гонок. Решение. Введем обозначения для логических высказываний:
Учитывая то, что предположения двух друзей подтвердились, а предположения третьего неверны, запишем и упростим истинное высказывание:
Высказывание истинно только при Ш=1, А=0, Х=0. Ответ. Победителем этапа гонок стал Шумахер.
Пример 2. В симфонический оркестр приняли на работу трёх музыкантов: Брауна, Смита и Вессона, умеющих играть на скрипке, флейте, альте, кларнете, гобое и трубе. Известно, что: 1. Смит самый высокий; 2. Играющий на скрипке меньше ростом играющего на флейте; 3. Играющие на скрипке и флейте и Браун любят пиццу; 4. Когда между альтистом и трубачом возникает ссора, Смит мирит их; 5. Браун не умеет играть ни на трубе, ни на гобое. На каких инструментах играет каждый из музыкантов, если каждый владеет двумя инструментами?
Решение. Составим таблицу и отразим в ней условия задачи, заполнив соответствующие клетки цифрами 0 и 1 в зависимости от того, ложно или истинно соответствующее высказывание. Ответ. Браун играет на альте и кларнете, Смит — на флейте и гобое, Вессон — на скрипке и трубе.
Пример 3. Три одноклассника — Влад, Тимур и Юра, встретились спустя 10 лет после окончания школы. Выяснилось, что один из них стал врачом, другой физиком, а третий юристом. Один полюбил туризм, другой бег, страсть третьего — регби. Юра сказал, что на туризм ему не хватает времени, хотя его сестра — единственный врач в семье, заядлый турист. Врач сказал, что он разделяет увлечение коллеги. Забавно, но у двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен. Определите, кто чем любит заниматься в свободное время и у кого какая профессия. Решение. Здесь исходные данные разбиваются на тройки (имя — профессия — увлечение). Ответ. Влад — юрист и регбист, Тимур — врач и турист, Юра — физик и бегун.
Пример 1. Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: "Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский". Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей? Решение. Имеется три утверждения: 1. Вадим изучает китайский; 2. Сергей не изучает китайский; 3. Михаил не изучает арабский. Если верно первое утверждение, то верно и второе, так как юноши изучают разные языки. Это противоречит условию задачи, поэтому первое утверждение ложно. Если верно второе утверждение, то первое и третье должны быть ложны. При этом получается, что никто не изучает китайский. Это противоречит условию, поэтому второе утверждение тоже ложно. Ответ. Сергей изучает китайский язык, Михаил — японский, Вадим — арабский. Пример 2. В клубе «Отдых» познакомились 3 любителя клубной музыки видов техно, хаус, рейв. Один говорит: «Вы какую музыку больше любите? Я техно люблю!». Другой ответил, что любит хаус, а третий сказал, что не любит ни техно, ни хаус, но зато обожает рейв. Интересно то, что все они были в банданах и рубашках черного, белого и желтого цветов, но цвет банданы и рубашки совпадал только у любителя техно. А у любителя хаус ни рубашка, ни бандана не были белыми. А любитель рейв был в желтой рубашке. Определите цвет рубашек и бандан каждого из любителей клубной музыки. Решение. Заметим, что по условию задачи цвет банданы и рубашки совпадал только у любителя техно. А так как у любителя хауса ни рубашка, ни бандана не были белыми, и любитель рейв был в желтой рубашке, то делаем вывод, что любитель техно может быть в рубашке и бандане только белого цвета. Ответ. У любителя техно рубашка и бандана белого цвета; у любителя хаус черная рубашка и желтая бандана; у любителя рейв желтая рубашка и черная бандана.
Пример 3. Атос, Портос и Арамис в соревновании по фехтованию заняли три первых места. Какое место занял каждый из них, если Портос занял не второе и не третье место, а Арамис – не третье? Решение. Учитывая условия задачи, сразу делаем вывод, что Портос занял первое место. Ответ. Арамис занял второе место, и Атос – третье место.
Пример 4. Коренными жителями острова являются рыцари света и рыцари тьмы. Рыцари света всегда говорят правду, а рыцари тьмы всегда лгут. Рыцарь А говорит: «Я – лжец». Является ли он уроженцем острова рыцарей света и рыцарей тьмы? Решение. Пусть А сказал правду, значит, он – рыцарь тьмы. Но он не может быть рыцарем тьмы, так как рыцари тьмы всегда лгут. Пусть А сказал ложь, тогда он рыцарь света. Но рыцари света говорят правду. Опять не получается. Значит, А не может быть уроженцем острова рыцарей света и рыцарей тьмы. Ответ. А не является уроженцем острова.
Пример 5. У короля было три дочери. Янка, Иванка и Бланка. Янка всегда говорила правду. Иванка иногда говорила правду, а иногда лгала, а Бланка всегда лгала. Ко двору короля пришел принц, чтобы просить руки правдивой Янки. Король привел его в зал, где все три принцессы сидели рядом, и сказал принцу, что отдаст ему Янку в жены, если принц сам узнает ее из трех принцесс. При этом принц может задать каждой из принцесс по одному вопросу. Принц задумался и потом задал каждой из принцесс один и тот же вопрос: "Как зовут принцессу, которая сидит в середине? " Принцесса, которая сидела слева, ответила: "Янка". Принцесса, сидевшая посередине, ответила: "Бланка". Принцесса, сидевшая справа, ответила: "Иванка". Выслушав ответы принцесс, принц узнал свою Янку. Где сидела Янка? Решение. Справа. Если Янка слева, то она солгала - ведь она не может сидеть в середине. Если Янка посередине, то она опять солгала. Если посередине бы сидела Бланка, то получилось бы, что она сказала правду, а это невозможно. Ответ. Значит, посередине Иванка, девушка справа сказал аправду, значит она Янка. Пример 6. На острове два города, в одном живут Эльфы, говорящие только правду, а в другом – Орки, говорящие только ложь. Встретились три существа А, В и С. Решение. Рассмотрим два случая. Ответ. В любом случае С – Орк.
Задачник 1. Три дочери писательницы Дорис Кей — Джуди, Айрис и Линда, тоже очень талантливы. Они приобрели известность в разных видах искусств — пении, балете и кино. Все они живут в разных городах, поэтому Дорис часто звонит им в Париж, Рим и Чикаго.
2. Пытаясь вспомнить победителей прошлогоднего турнира, пять бывших зрителей турнира заявили:
3. В школе, перешедшей на самообслуживание, четырем старшеклассникам: Андрееву, Костину, Савельеву и Давыдову поручили убрать 7-ой, 8-ой, 9-ый и 10-ый классы. При проверке оказалось, что 10-ый класс убран плохо. Не ушедшие домой ученики сообщили о следующем:
4. Пять школьников из пяти различных городов Брянской области прибыли для участия в областной олимпиаде по математике. На вопрос: «Откуда Вы?» каждый дал ответ:
5. На соревнованиях по легкой атлетике Андрей, Борис, Сергей и Володя заняли первые четыре места. Но когда девочки стали вспоминать, как эти места распределились между победителями, то мнения разошлись.
6. Кто из друзей (Иван, Петр, Алексей, Николай или Борис) коллекционирует марки, если известно, что:
7. На вопрос, кто из трех абитуриентов A, B, C может работать на компьютере, был получен ответ: если может работать B, то может работать и C, но не верно, что если может работать A, то может работать и C. Кто из трех абитуриентов может работать на персональном компьютере?
8. На вопрос, какая завтра погода, синоптик ответил: если не будет ветра, то будет пасмурная погода без дождя; если будет дождь, то будет пасмурно и без ветра; если будет пасмурно, то будет дождь и не будет ветра. Подумав немного, синоптик уточнил, что его три высказывания можно записать более лаконично. Попробуйте это сделать!
9. На олимпиаде по информатике студенты A, B, C и D заняли первые четыре места. Когда их спросили о распределении мест, они дали три ответа: D – первый или B – второй; C – первый или A – четвертый; D – второй или B – третий. Как распределились места, если в каждом ответе только одно утверждение истинно?
10. Кто из абитуриентов A, B, C и D играет, а кто не играет в шахматы, если известно следующее: если A или B играет, то C не играет; если B не играет, то играют C и B; C – играет. Решить задачу с помощью логических операций.
11. В деле об убийстве имеются двое подозреваемых: A и B. Допросили четверых свидетелей. Показания первого таковы: «A не виноват». Второй свидетель сказал: «B не виноват». Третий свидетель: «Из двух показаний по крайней мере одно истинно». Четвертый: «Показания третьего свидетеля ложны». Четвертый свидетель оказался прав. Кто же совершил преступление?
12. Аня, Вика и Сергей решили пойти в кино. Учитель хорошо знавший этих ребят, высказал следующие предположения: Аня пойдет в кино только тогда, когда пойдут Вика и Сергей; Аня и Сергей пойдут в кино вместе или же оба останутся дома; чтобы Сергей пошел в кино, необходимо, чтобы пошла Вика. Когда ребята пошли в кино, оказалось, что учитель немного ошибался, из трех его утверждений истинными оказались только два. Кто из названных ребят пошел в кино?
13. Костя пригласил свою сестру приехать к нему в гости. После этого он получил от нее три сообщения: я приеду в гости, если только со мной приедет папа; чтобы я приехала, необходимо, чтобы меня сопровождала мама; либо приедем мы с мамой, либо приедет только папа. Когда приехали гости, оказалось, что из этих трех сообщений истинным было только одно. Кто приехал навестить Костю?
14. Студенты узнали, что к ним в группу должен придти юноша из другого института. Обсуждая эту новость, студенты высказали ряд предположений: для того, чтобы новичок был добрым, достаточно чтобы он был умным; если новичок силач, то он либо глупый, либо злой; если новичок умный, то для того, чтобы он был добрым, необходимо, чтобы он бы сильным. Преподаватель сказал, что из этих условий выполнено только одно. Кроме того, преподаватель сказал: «Необходимое условие доброты – это ум. Значит, новичок умный, но слабый». Каким был новичок?
15. Пятеро друзей.
16. Обед с логикой.
17. Диагностическая.
18. Экономическая.
19. Для полярной экспедиции из восьми претендентов A, B, C, D, E, F, G, H надо отобрать шесть специалистов: биолога, гидролога, синоптика, радиста, механика и врача. Обязанности биолога могут выполнять E и G, гидролога – B и F, синоптика F и G, радиста – C и D, механика C и H, врача A и D. Хотя некоторые претенденты владеют двумя специальностями, в экспедиции сможет выполнять только одну. Кого и кем следует взять в экспедицию, если F не может ехать без B, D – без H и без C, C не может ехать одновременно с G, а A не может ехать вместе с B?
20. Спортивная.
21. Коробочки
22. На десяти карточках написано по одному целому числу от 1 до 10. Пятеро людей вытягивали по две карточки и называли сумму чисел. В итоге известно, что получились следующие суммы:
23. Среди гостей присутствуют пять офицеров: пехотинец, артиллерист, летчик, связист и сапер. Один из них – капитан, трое – майоры и один – подполковник. Известно, что:
24. В библиотеке не хватает пяти книг:
25. Посл
|
||||
|
Последнее изменение этой страницы: 2016-12-26; просмотров: 3334; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.163.23 (0.012 с.) |

 Очевидно, что высказывание А – истинно, а высказывание В – ложно. Существуют разные варианты обозначения истинности и ложности переменных:
Очевидно, что высказывание А – истинно, а высказывание В – ложно. Существуют разные варианты обозначения истинности и ложности переменных: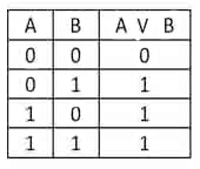 В математике: если каждое выражение совокупности взять за отдельное высказывание то составное высказывание, образованное логическим сложением, будет являться решением этой совокупности.
В математике: если каждое выражение совокупности взять за отдельное высказывание то составное высказывание, образованное логическим сложением, будет являться решением этой совокупности.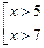 пусть высказывание А – х>5, а высказывание В – х>7 тогда
пусть высказывание А – х>5, а высказывание В – х>7 тогда  это составное высказывание
это составное высказывание  т.е. х>5
т.е. х>5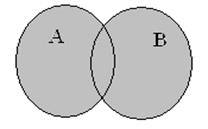 Итак, высказывание AˇB можно представить в виде объединения множеств А и В:
Итак, высказывание AˇB можно представить в виде объединения множеств А и В:
 C.
C.
 - отрицание логического произведения эквивалентно логической сумме отрицаний множителей.
- отрицание логического произведения эквивалентно логической сумме отрицаний множителей. - отрицание логической суммы эквивалентно логическому произведению отрицаний слагаемых.
- отрицание логической суммы эквивалентно логическому произведению отрицаний слагаемых. Ú U) º
Ú U) º











