
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напряженность электростатического поляСодержание книги
Поиск на нашем сайте Электрическое поле действует только на электрические заряды. Поэтому обнаружить электрическое поле можно только с помощью внесения в интересующую нас точку пространства пробного заряда. Величина пробного заряда должна быть очень малой по сравнению с зарядом, создающим поле. В качестве пробного заряда условились использовать положительный заряд. Силы, действующие на один и тот же пробный заряд в различных точках электрического поля, отличаются величиной и направлением. Отношение Размерность напряженности электрического поля: Принцип суперпозиции электростатических полей: если электрическое поле создается несколькими зарядами, то напряженность результирующего поля является векторной суммой напряженностей, создаваемых отдельными зарядами.
Фарадей предложил изображать электрическое поле силовыми линиями (линиями напряженности). Силовой линией называется такая линия, по касательной к каждой точке которой направлены векторы напряженности электрического поля в данной точке. Силовые линии некоторых заряженных тел приведены на рисунке 2. Свойства силовых линий (линий напряженности):

Теорема Гаусса для электростатического поля в вакууме Поток вектора напряженности электрического поля через элементарную площадку
Рисунок 3. Поток вектора напряженности через элементарную площадку.
Для произвольной замкнутой поверхности S поток вектора Поток вектора напряженности — алгебраическая величина, т.е. зависит не только от конфигурации потока Е, но и от выбора направления нормали Поток вектора напряженности сквозь сферическую поверхность радиуса r (с площадью поверхности

Формула справедлива для замкнутой поверхности любой формы. Если замкнутая поверхность не охватывает заряда, то поток вектора напряженности через нее равен 0. Если замкнутая поверхность охватывает n зарядов, и каждый заряд создает поток
— т еорема Гаусса в Интегральном виде Поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на диэлектрическую проницаемость вакуума
|
||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 191; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.86.209 (0.009 с.) |

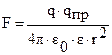
 не зависит от величины пробного заряда
не зависит от величины пробного заряда  и поэтому является силовой характеристикой электрического поля, созданного точечным зарядом
и поэтому является силовой характеристикой электрического поля, созданного точечным зарядом  . Это отношение называется напряженностью электрического поля
. Это отношение называется напряженностью электрического поля  . Модуль напряженности, создаваемой точечным зарядом:
. Модуль напряженности, создаваемой точечным зарядом:  .
. .
.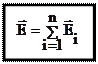 — принцип суперпозиции (наложения) электростатических полей. Принцип суперпозиции позволяет рассчитывать электростатические поля любой системы неподвижных зарядов.
— принцип суперпозиции (наложения) электростатических полей. Принцип суперпозиции позволяет рассчитывать электростатические поля любой системы неподвижных зарядов.

 :
:  (рисунок 3), где
(рисунок 3), где — проекция вектора
— проекция вектора  на нормаль
на нормаль 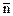 к площадке dS.
к площадке dS.
 — интеграл по замкнутой поверхности S.
— интеграл по замкнутой поверхности S. . Для замкнутых поверхностей за положительное направление нормали принимается внешняя нормаль, т.е. нормаль, направленная наружу области, охваченной поверхностью.
. Для замкнутых поверхностей за положительное направление нормали принимается внешняя нормаль, т.е. нормаль, направленная наружу области, охваченной поверхностью. ), охватывающую точечный заряд q, находящейся в ее центре:
), охватывающую точечный заряд q, находящейся в ее центре: .
.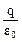 , то в соответствии с принципом суперпозиции общий поток вектора напряженности через замкнутую поверхность:
, то в соответствии с принципом суперпозиции общий поток вектора напряженности через замкнутую поверхность: 

 .
.


